дифуравнения / дифуравнения-1 / тема1

Тема: Диференціальні рівняння першого порядку. Рівняння з подільними

змінними.

Теоретичні відомості.

Диференціальне рівняння І порядку в загальному вигляді може бути записане так: . Якщо таке рівняння розрішити відносно похідної , то його можна подати у вигляді .

Загальним рішенням (загальним інтегралом) рівняння першого порядку є функція , , яка задовольняє рівнянню при будь – яких значеннях довільної константи .

Отже, для знаходження частинного рішення рівняння І порядку слід знайти значення лише однієї константи . Для цього достатньо задати єдину початкову умову , розв’язати задачу Коші і знайдене значення підставити в загальне рішення. В результаті отримаємо частинне рішення , яке задовольняє початковій умові .

Розглянемо основні типи диференціальних рівнянь І порядку.

2.1. Рівняння , яке може бути розв’язане шляхом простого інтегрування обох частин рівняння, тобто .

2.2. Рівняння з подільними змінними

Означення. Диференціальним рівнянням з подільними змінними називається рівняння

, (1.1)

або

. (1.2)

Поділимо обидві частини рівняння (1.1) на добуток і отримаємо рівняння

. (1.3)

Позначимо , тоді перейдемо к рівнянню з поділеними змінними, в якому кожне з двох доданків в лівій частині залежить лише від однієї змінної. Інтегруючи почленно останню рівність, знайдемо загальний інтеграл даного рівняння .

Практичні завдання.

1. Рівняння виду

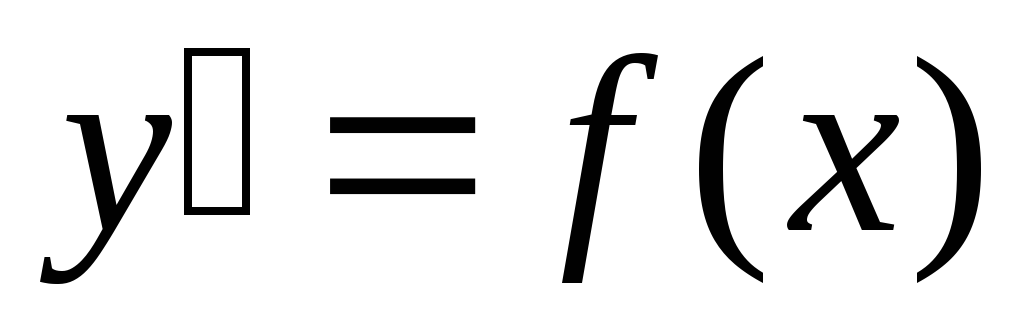
Знайти інтеграл (рішення) диференціального рівняння:

1.1. , якщо .

1.2 .

1.3. , якщо .

2. Рівняння з подільними змінними

Проінтегрувати рівняння:

2.1. .

2.2. .

2.3. .

2.4. .

2.5. .

2.6. .

2.7. .

2.8. .

Розв’язати задачу Коші:

2.9. , якщо .

2.10. , якщо .

2.11. , якщо .

2.12. , якщо .

2.13. , якщо .

2.14. , якщо .

2.15. , якщо .

Домашнє завдання: теоретичні відомості

Знайти загальний інтеграл рівняння

1. .

2. .

Знайти частинний інтеграл рівняння , якщо .