4. Смешанные стратегии

Седловая точка в матричных играх всё-таки скорее исключение, чем правило. А что же может гарантировать себе игрок, если седловой точки нет?

Давайте снова рассмотрим игру с платёжной матрицей

.

Здесь , и между  и  образуется “дыра” Как можно её заполнить и чем?

Представим себя в позиции первого игрока. Он имеет гарантированный выигрыш (скорее, проигрыш), равный (-1). Как он может его повысить?

Конечно, если игра повторяется много раз, то он может изучить своего партнёра, придумывать всякие схемы игры и т.д. и т.п., но вряд ли это даст какие-то гарантии, если число партий невелико. Тут никакие схемы не помогут.

В такой ситуации единственный выход  выбирать свой ход случайным образом. Например, взять и подбросить монету. Упадёт она кверху орлом  делать ход i=1, выпадет решка  делать ход i=2. Что же это даст?

Выигрыш станет случайной величиной и оценивать его надо по математическому ожиданию. Пусть второй игрок делает ход j=1. Тогда математическое ожидание выигрыша первого игрока будет

.

Если второй игрок делает ход j=2, то математическое ожидание выигрыша первого игрока равно

.

Таким образом, выбирая свой ход случайно, первый игрок гарантирует себе (правда, в среднем, а не в каждой партии), выигрыш, равный нулю. А это всё-таки лучше, чем гарантированный выигрыш, равный (-1) .

Аналогично, второй игрок, бросая монету и выбирая ход в соответствии с её “указанием”, гарантирует себе в среднем проигрыш, равный 0. Это тоже лучше, чем проигрыш, равный 1.

Таким образом, оказывается, что случайный выбор хода повышает наши шансы на успех, хотя бы в среднем. И это является одной из основных идей теории игр  выбиратьсвой ход случайно. Подобный случайный выбор хода получил название смешанной стратегии.

Конечно, с обычных житейских позиций, случайный выбор хода не всегда приемлем. Вообразите себе военачальника, который выиграл сражение. Он даёт интервью по TV и на вопрос о том, как же он принял правильное решение, говорит: “Ну, я бросил монету, она упала орлом кверху, и поэтому я … ”. Как посмотрит на него телезритель? А если он проиграл битву, то как отнесётся к такому ответу его начальство?

И тем не менее, случайный выбор хода  смешанная стратегия  имеет право на существование, даже в реальной жизни. Когда не знаешь, как действовать  выбирай свой ход случайным образом! Иногда помогает. По крайней мере, никто не разгадает стратегии твоего поведения и не предугадает твоего хода.

7. Игры двух лиц с ненулевой суммой

Рассмотрим теперь основные идеи, касающиеся игр двух лиц с ненулевой суммой. В этом случае игра задаётся двумя матрицами, которые обычно объединяют в одну и пишут в виде

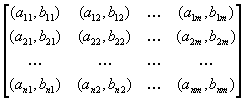
Здесь  выигрыш первого игрока и  выигрыш второго, если первый игрок делает ход i, а второй  j. Однако в данном случае 

В такой ситуации появляется принципиально новый момент, которого не было раньше  возможность сговора, совместных действий игроков. Когда , то интересы обоих игроков прямо противоположны ивозможность сговора исключена в силу противоположности интересов. Если , то интересы игроков могут хотя бы частично совпадать, что и определяет возможность хотя бы частичного сотрудничества между ними.

И эта возможность сговора не упрощает, а сильно усложняет ситуацию! Потому, что до чего и как договорятся игроки в очень сильной степени зависит от двух вещей: от самой возможности вести переговоры и от психологических особенностей игроков. А психология  очень сложная вещь и математика до неё еще не добралась.

Игры двух лиц с ненулевой суммой принято разбивать на два класса  некооперативные и кооперативные. В некооперативных играх игроки не имеют возможности общаться друг с другом. Как же они могут договориться между собой? Это возможно, если игра повторяется  тогда возможность такого сговора появляется в ходе повторения игры, ведь можно наказывать партнёра, выбирая заведомо плохой для него ход. Но вот что из этого получится  теория игр пока не даёт ни ответа, ни совета.

В кооперативных играх игроки имеют возможность договариваться в любое удобное для них время и никаких косвенных приёмов для договорённостей им применять не надо.

Игры против природы – наши критерии

Особое место в теории игр занимают игры против природы, которые ещё носят название выбора решений при неопределённости. Природа хотя и делает случайные ходы, но не является злонамеренным игроком, так как она не стремится сделать как можно хуже своему противнику и не обладает разумом. Поэтому и выбор решения в такой ситуации имеет свои особенности.

11.3.3 Обгрунтування рішень на основі змішаних стратегій

В економічній практиці у більшості ігор сідлова точка у чистих стратегіях відсутня, що не дозволяє однозначно визначити оптимальні стратегії гравців. В таких випадках використовуються змішані стратегії, у яких випадковим чином чергуються особисті стратегії. Цей метод широко використовується в господарській практиці, що виражається у стратегії диверсифікації. Наприклад, виробники, не знаючи заздалегідь точних даних щодо попиту, прагнуть розширити асортимент продукції; інвестори вкладають кошти у різні цінні папери і т. д. Отже, гравці намагаються отримати максимальний виграш (мінімальний програш), застосовуючи не одну, а кілька стратегій.

Точний метод знаходження оптимальної змішаної стратегії зводиться до задачі лінійного програмування, який досить трудомісткий. Існують спеціальні комп᾽ютерні програми, що реалізують цей метод [машина, сороки, дубров, клименко, ивченко]. Однак можна спробувати знайти оптимальне рішення в умовах конфлікту на основі змішаних стратегій.

Змішана стратегія гравця – це повний набір застосування його чистих стратегій при багаторазовому повторенні гри в тих самих умовах із заданими ймовірностями.

Умови застосування змішаних стратегій:

• гра не має сідлової точки;

• гравці використовують випадкове поєднання чистих стратегій із заданими ймовірностями;

• гра багаторазово повторюється в подібних умовах;

• при кожному з ходів жоден гравець не інформований про вибір стратегії іншим гравцем;

• допускається осереднення результатів ігор [машина, сороки, клименко].

При використанні змішаних стратегій використовують наступні основні положення, наведені у [машина, сороки, дубров, клименко, ивченко].

Для гравця А змішана стратегія полягає в застосуванні чистих стратегій А₁, А₂, …А_m з відповідними ймовірностями р₁, р₂, …р_m позначається матрицею

,

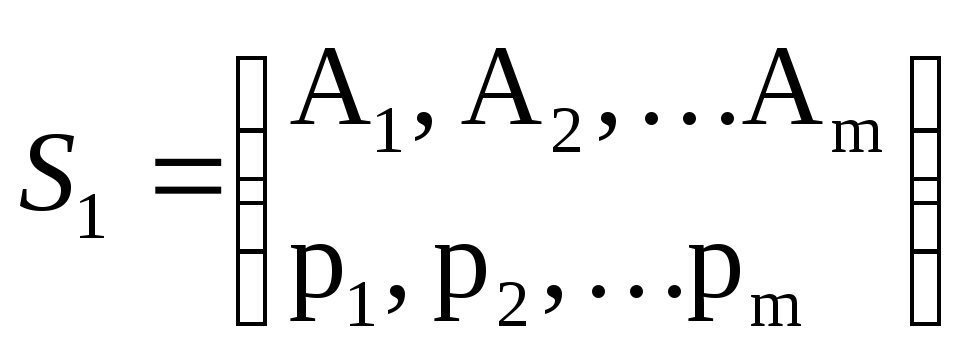за умови, що

Для гравця В

,

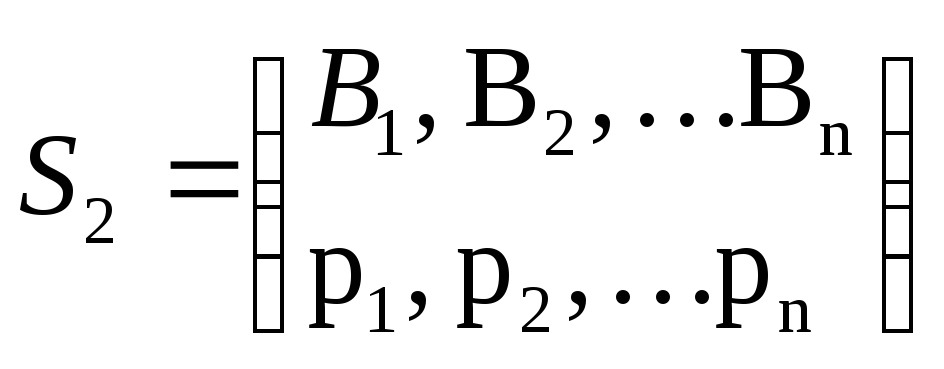за умови, що , де– ймовірність застосування чистої стратегіїВ_j.

В окремому випадку, коли , для гравця А маємо чисту стратегію:

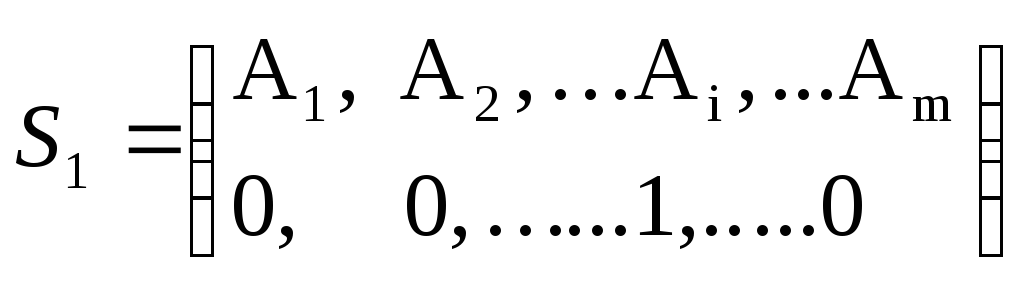
Чисті стратегії гравця є єдино можливими неспільними подіями [сороки, клименкоУчебник]. У матричній грі при заданих векторах іможна визначити середній виграш гравцяА:

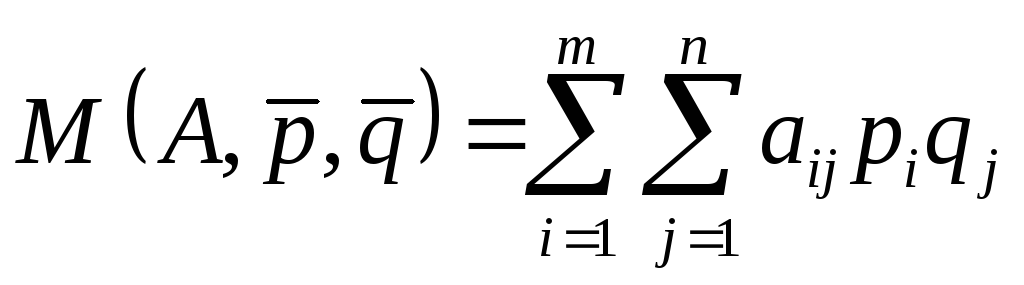
де і– вектори відповідних ймовірностей;

і – компоненти цих векторів.

Шляхом застосування своїх мішаних стратегій гравець А прагне максимально збільшити свій середній виграш, а гравець В – мінімізувати виграш гравця А. Гравець А прагне досягти виконання умови:

Гравець В домагається виконання протилежної умови:

Вектори, що відповідають оптимальним мішаним стратегіям гравців А і В, позначимо як і. Для цих векторів виконується рівність:

Ціна гри – середній виграш гравця А при використанні обома гравцями змішаних стратегій.

Розв᾽язком матричної гри є оптимальна змішана стратегія гравця А (); оптимальна змішана стратегія гравця В () та ціна гри ().

Змішані стратегії будуть оптимальними (і), якщо вони утворюють сідлову точку для функції, тобто

.

Основна теорема теорії ігор. Для матричної гри з будь-якою матрицею А величини ііснують, вони рівні між собою і дорівнюють ціні гри:.

При виборі оптимальних стратегій гравцю А завжди буде гарантований середній виграш, не менший, ніж ціна гри, за будь-якої фіксованої стратегії гравця В (а для гравця В - навпаки).

Активними стратегіями гравців А і В називають стратегії, що входять до складу оптимальних змішаних стратегій відповідних гравців з ймовірностями, відмінними від нуля. Отже, до складу оптимальних змішаних стратегій можуть входити не всі апріорі задані їх стратегії.

Розглянемо окремий випадок розв᾽язання задач на основі змішаних стратегій. Найпростіша гра може бути описана матрицею 22. За відсутності сідлової точки можна отримати дві оптимальні змішані стратегії, які записуються так:

; .

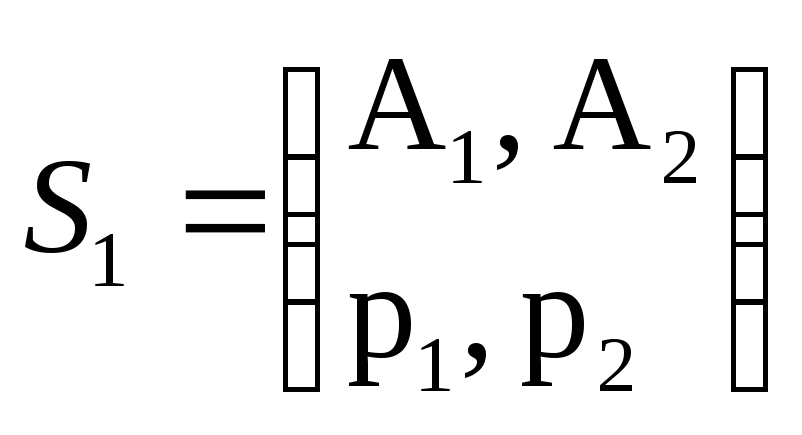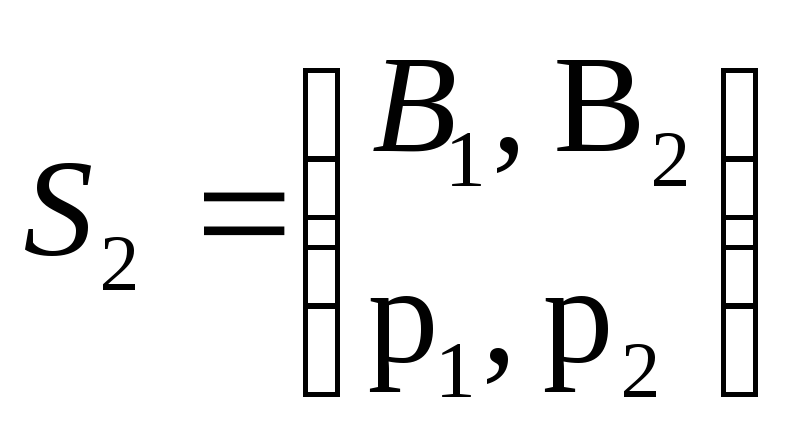Отже, є платіжна матриця:

.

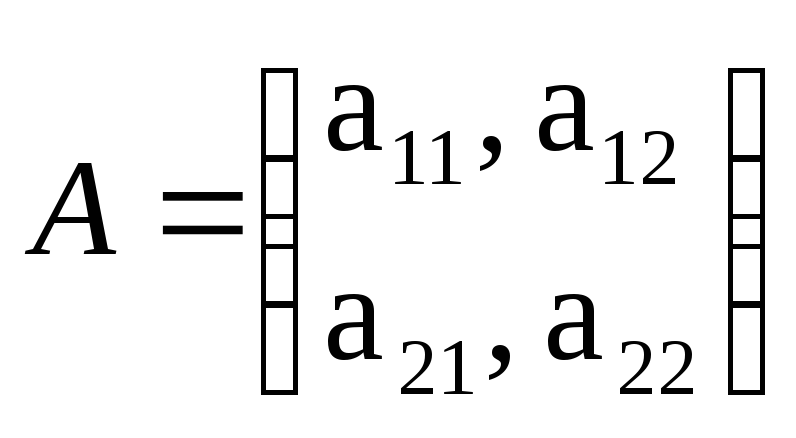При цьому

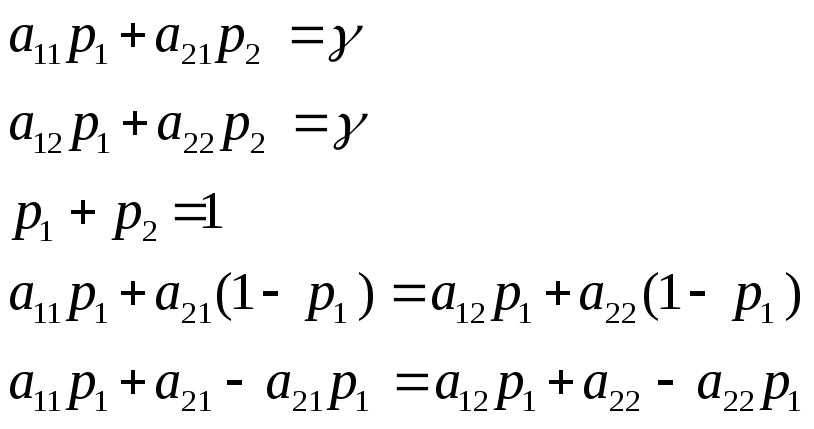
звідки одержуємо оптимальні значення та.

Знаючи та, знаходимо:

Обчисливши , знаходимота:

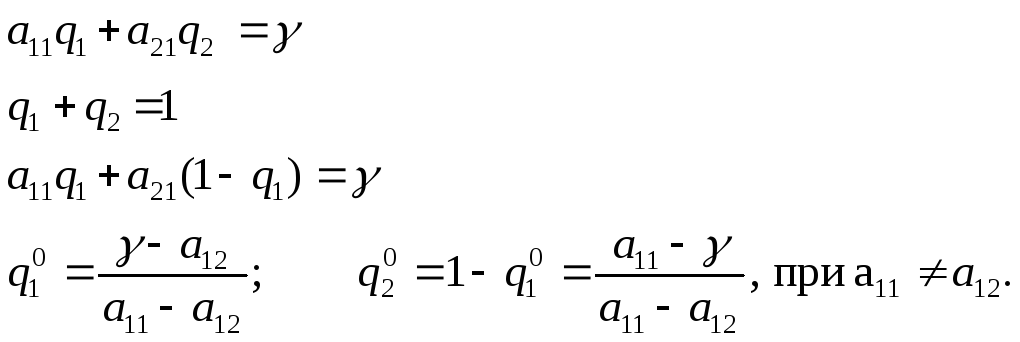
Задачу розв᾽язано, оскільки знайдено вектори і ціна гри.

Це завдання можна розв᾽язати графічним методом, використовуючи наступний алгоритм:

• по осі абсцис відкладається відрізок одиничної довжини;

• по осі ординат відклажаються виграші при стратегії А₁;

• на лінії, паралельній осі ординат, у точці 1 відкладаються виграші при стратегії А₂;

• кінці відрізків позначаються для ,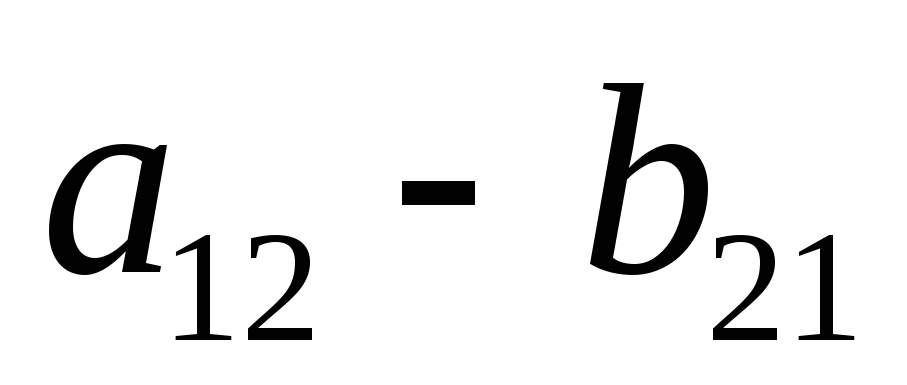;;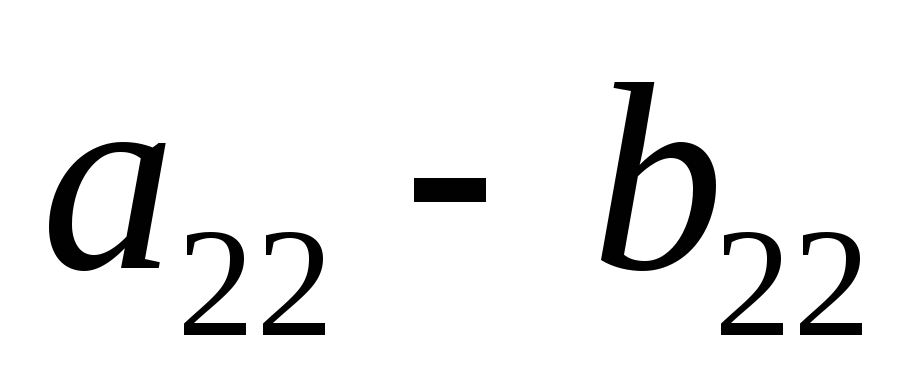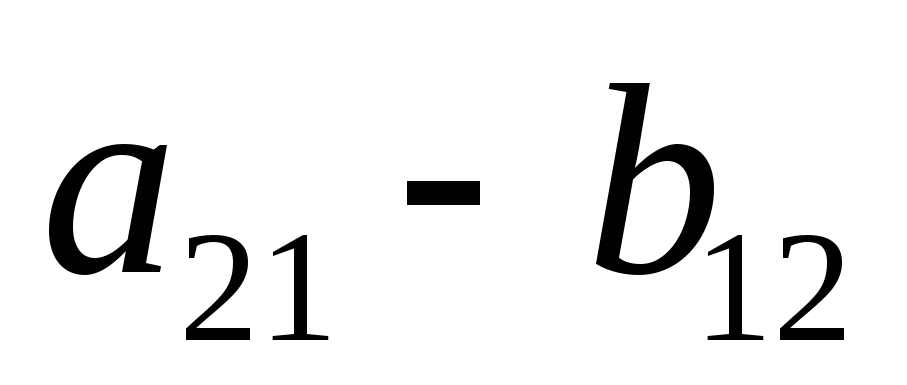та проводяться прямі лінії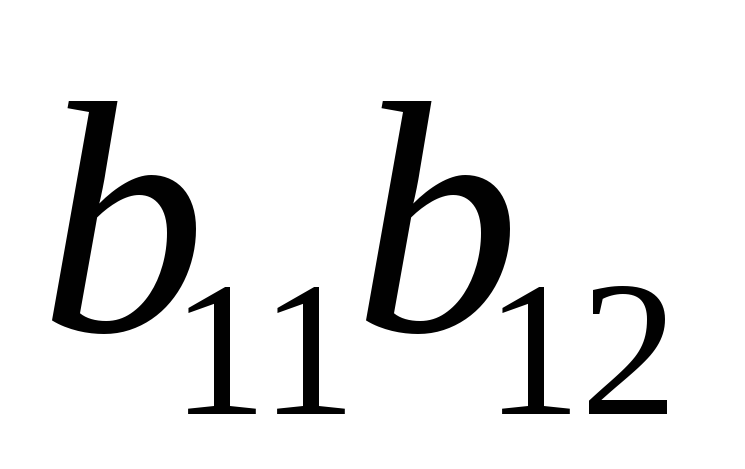та;

• визначається ордината точки перетину проведених прямих ліній, яка позначається с. Висота перпендикуляру, опущеного з цієї точки на ось абсцис, дорівнює . Абсциса точкис дорівнює ().

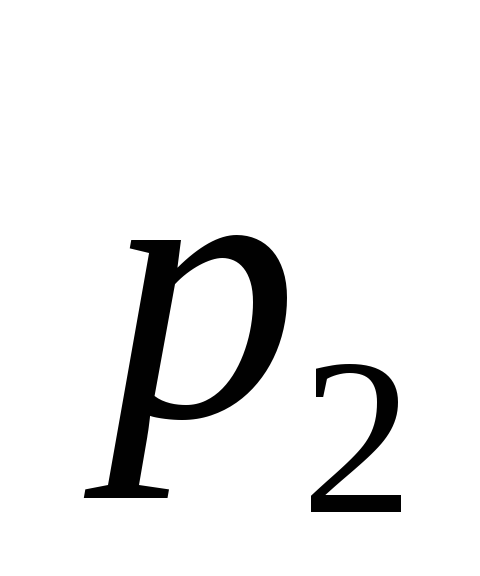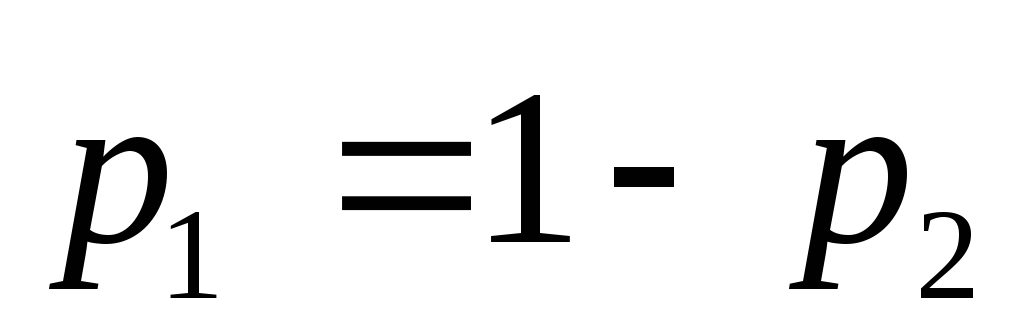Графічне зображення цього алгоритму наведено на рисунку 11.1.

Рисунок 11.1 – Графічний метод знаходження оптимальної змішаної стратегії

Даний метод має досить широку сферу використання, що огрунтується на загальній властивості ігор , яка полягає в тому, що у будь-якій грікожен гравець має оптимальну змішану стратегію, у якій кількість чистих стратегій не перевищує. З цієї властивості випливає, що у будь-якій грітакожна оптимальна стратегіятамістить не більш двох активних стратегій. Отже, будь-яка граабоможе бути зведена до гри 22 та розв᾽язана графічним методом. Якщо матриця скінченної гри має розмірність, деі, то для визначення оптимальних змішаних стратегій використовується лінійне програмування. Опис цього розв᾽язання докладно описаний у [івченко, с153].

Контрольні питання

1 Поняття конфліктної ситуації. Причини виникнення конфліктних ситуацій.

2 Особливості розв᾽язання завдань в умовах невизначеності та конфлікту.

3 Система понять теорії ігор.

4 Сутність мажорування стратегій гравців.

5 Порядок обгрунтування рішень на основі чистих стратегій

6 Способи вибору рішень на основі змішаних стратегій.