Тема 10 критерії прийняття господарських рішень за умов ризику

Як зазначалося в попередніх розділах (див. розділ 7.1), відмінною рисою прийняття рішень в умовах ризику є наявність даних щодо оцінки ймовірності результатів різних варіантів рішення. При цьому виходять з припущення, що сума ймовірностей станів економічного середовища дорівнює одиниці. Це означає, що враховуються всі можливі стани економічного середовища.

Для обгрунтування господарських рішень в умовах ризику застосовуються наступні критерії:

• критерій математичного сподівання (критерій Байєса);

• критерій стандартного відхилення;

• критерій Бернулі;

• критерій Лапласа;

• критерій Гурвіца.

10.1 Критерій математичного сподівання (критерій Байєса)

Критерій математичного сподівання (критерій Байєса) передбачає вибір оптимального варіанта господарського рішення на основі результатів розрахунку усереднених значень узагальнюючих економічних показників, що характеризують наявні варіанти рішення. Як узагальнюючі економічні показники варіантів рішення найчастіше розглядаються дохід, прибуток, витрати, вартість капіталу, втрати, недоотриманий прибуток і т. д.

Відповідно до критерію Байєса за кожним варіантом рішення обчислюють середньозважене значення обраного узагальнюючого економічного показника з урахуванням ймовірностей станів економічного середовища. Вихідні дані для розрахунку отримують з матриці виграшів або матриці ризиків.

Якщо аналізуються дані матриці виграшів, то усереднюваними показниками є дохід або прибуток. Оптимальним варіантом рішення вважається той, за яким величина математичного сподівання є максимальною. Реалізація цього варіанту рішення забезпечить отримання максимального доходу (прибутку).

Стратегія, що передбачає реалізацію обраного оптимального варіанту рішення, називається байєсівською стратегією. Величина узагальнюючого економічного показника, яка відповідає обраному оптимальному варіанту рішення, називається байєсівською оцінкою [витл].

За даними матриці ризиків обчислюють середньозважені значення можливих втрат (збитків, недоотриманого прибутку) за варіантами рішення. Оптимальний варіант рішення визначають за мінімальним середньозваженим значенням збитків або недоотриманого прибутку. Такий варіант передбачає мінімізацію втрат при реалізації рішення.

Мінімальну середньозважену величину можливих збитків (недоотриманих прибутків) називають байєсівським ризиком рішення [витл].

Критерій Байєса враховує всі можливі стани економічного середовища, отже, він є досить інформативним. Тому у випадках, коли використання інших критеріїв призводить до суперечливих висновків, при формуванні остаточного висновку рекомендується надавати перевагу саме критерію Байєса.

1) Критерий Байеса (максимум среднего выигрыша):

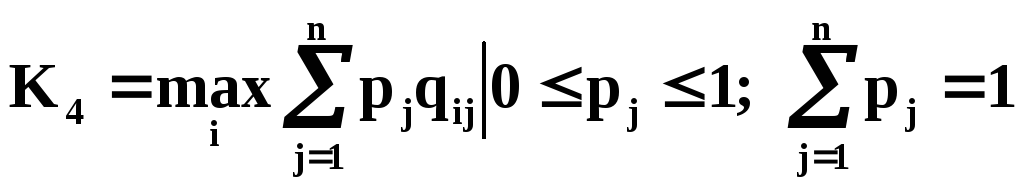
2) Критерий Байеса-Севиджа (минимального среднего риска):

10.2 Критерій Лапласа

Критерій Лапласа використовується у випадку, коли можна припустити, що кожний з можливих станів економічного середовища є не більш ймовірним, ніж інші. Тоді можна припустити, що всі можливі варіанти стану економічного середовища мають однакову ймовірність, що становить сутність принципу «недостатнього обгрунтування», запропонованого Байєсом у 1763 р., та узагальненого Лапласом у 1812 р. [дубров].

Критерий Байеса-Лапласа (принцип недостаточной подстановки):

Критерий Байеса (Лапласа) исходит из того, что если совершенно неизвестно, какое из состояний имеет место, то нужно поступать так, как будто они равновероятны.

Відповідно до критерію Лапласа вибір рішення здійснюється за мінімумом середньозваженого показника ризику (), який обчислюється за формулою:

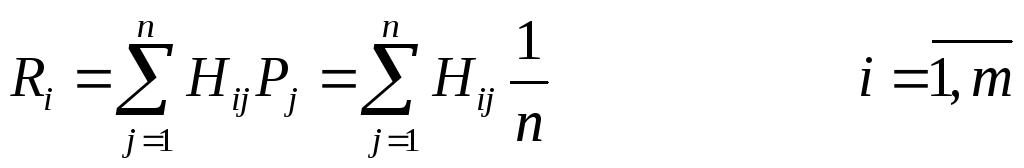(10.3)

де n – кількість варіантів стану економічного середовища;

–ймовірність j -го стану економічного середовища.

- втрати (недоотриманий прибуток) при i-му варіанті рішення та j-му варіанті стану економічного середовища.

Вихідні дані для розрахунку отримують з матриці ризику. За кожним варіантом рішення розраховуються середньозважені оцінки можливих збитків (недоотриманого прибутку). Отже, критерій Лапласа дозволяє мінімізувати можливі втрати підчас реалізації рішення.

Критерій Лапласа передбачає врахування ймовірностей всіх можливих станів економічного середовища, що свідчить на користь цього критерію.

Слід зазначити, що критерій Лапласа може використовуватись як в умовах ризику, коли ймовірності станів економічного середовища відомі, так і в умовах невизначеності, коли інформація про ймовірності станів середовища відсутня. В першому випадку значення критерію Лапласа збігатиметься зі значенням критерію Байєса (байєсівським ризиком). Але висновок щодо варіанту рішення, якому доцільно надати перевагу, а також величина середньозваженої оцінки ризику в умовах ризику та в умовах невизначеності можуть відрізнятися.

10.3 Критерій Гурвіца

Цей критерій є спрощеним варіантом критеріїв Байєса та Лапласа. Для обчислення критерію Гурвіца можна скористатися формулою (7.4), якщо розрахунок проводиться за даними матриці виграшів.

Критерий Гурвица:

Коэффициент χ отображает меру пессимизма ЛПР.

10.4 Критерій стандартного відхилення

Використання критерію стандартного відхилення передбачає оцінку ступеня розсіяння (коливання) окремих значень того чи іншого узагальнюючого економічного показника рішення, що приймається, навколо його середнього значення. Чим більше розкид окремих значень економічного показника навколо його середнього значення, тим більша величина стандартного відхилення. Відповідно, більшою є невизначеність відносно того, що даний економічний показник набуватиме очікуваного значення, отже, і більший ризик.

Стандартне відхилення обчислюється за формулою:

(10.1)

де – дисперсія випадкової величини;

–окремі значення, яких набуває випадкова величина;

–математичне сподівання випадкової величини;

–ймовірності станів економічного середовища.

Для обчислення стандартного відхилення як вихідні дані використовуються окремі значення узагальнюючого економічного показника та його середнє значення (математичне сподівання) за кожним варіантом рішення. Найменш ризикованим вважається той варіант рішення, за яким значення стандартного відхилення є мінімальним.

Критерий компромисса Гурвица:

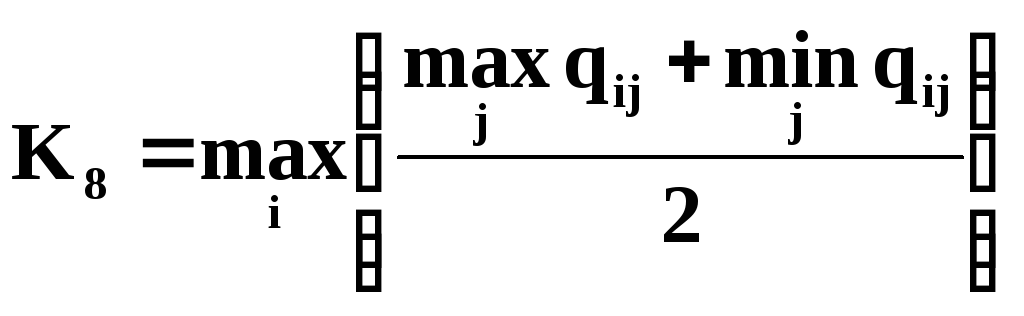
Критерий компромисса Гурвица согласно с риском:

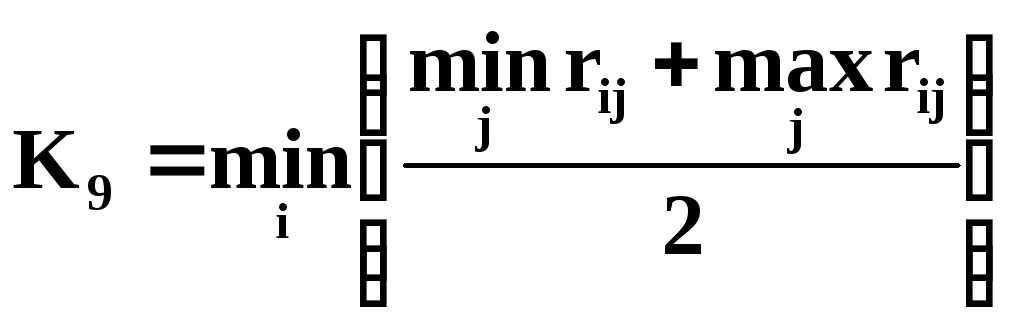
Критерий «труса»:

Критерий осторожности согласно с риском:

Критерий Гермейера: