Попит на хліб на добу

Попит на добу, шт.	10	12	14	16	18
Ймовірність	0,1	0,2	0,3	0,3	0,1

Якщо булка виготовлена, але не продана, то додаткові збитки становлять 0,20 грн. за штуку.

Потрібно побудувати платіжну матрицю доходів та матрицю ризиків і за допомогою різних критеріїв визначити, яку кількість продукції необхідно випускати пекарні.

1. Строим платежную матрицу:

Платежная матрица			продали
			в1	в2	в3	в4	в5
			10	12	14	16	18
произвели	10	а1	2	2	2	2	2
	12	а2	-0,2	2,4	2,4	2,4	2,4
	14	а3	-2,4	0,2	2,8	2,8	2,8
	16	а4	-4,6	-2	0,6	3,2	3,2
	18	а5	-6,8	-4,2	-1,6	1	3,6
		Max	2	2,4	2,8	3,2	3,6

Каждая ячейка = Цена * продали – С/с * произвели – Разница между произвели и продали (если она есть) * дополнительные расходы

2. Строим матрицу рисков

Матрица рисков			продали
			в1	в2	в3	в4	в5
произвели	10	а1	0	0,4	0,8	1,2	1,6
	12	а2	2,2	0	0,4	0,8	1,2
	14	а3	4,4	2,2	0	0,4	0,8
	16	а4	6,6	4,4	2,2	0	0,4
	18	а5	8,8	6,6	4,4	2,2	0

Каждая ячейка = максимальное значение по столбцу из платежной матрицы – значение ячейки платежной матрицы

При прийнятті рішень в умовах невизначеності для вибору рішень використовуються наступні критерії: критерій Вальда, критерій максимакс, критерій Севіджа, критерій Гурвіца.

7.2 Характеристика критеріїв прийняття рішень в умовах невизначеності

7.2.1 Критерій Вальда

Критерій Вальда (Максимінний) дозволяє обрати варіант рішення, який гарантує отримання максимально можливого виграшу за найгірших умов економічного середовища. Формалізований вираз цього критерію має вигляд:

(7.1)

Наш пример:

Платежная матрица		продали
		в1	в2	в3	в4	в5	мин
произвели	а1	2	2	2	2	2	2
	а2	-0,2	2,4	2,4	2,4	2,4	-0,2
	а3	-2,4	0,2	2,8	2,8	2,8	-2,4
	а4	-4,6	-2	0,6	3,2	3,2	-4,6
	а5	-6,8	-4,2	-1,6	1	3,6	-6,8
	Max	2	2,4	2,8	3,2	3,6

Выбираем минимальные значения результата (минимальная прибыль или максимальный убыток) из всех вариантов производств – и из них выбираем максимальное значение – это и есть вариант производства.

Ответ: мы производим минимум – 10 булок - потому что в этом случае мы понесем минимальные убытки при самом плохом варианте продаж.

Вихідними даними при виборі варіантів рішень за критерієм Вальда є виграші а_ij, що відповідають кожному зі сполучень рішень і стану економічного середовища, наведені в матриці виграшів. За кожним варіантом рішення визначають мінімальне значення виграшу. Потім з обраних мінімальних значень виграшу знаходять максимальну величину, яка дозволяє визначити варіант рішення, що дозволить отримати максимально можливий виграш за найгірших умов економічного середовища. Цей варіант рішення вважається оптимальним за даним критерієм.

Критерій Вальда орієнтує особу, що приймає рішення, на дуже обережну (песимістичну) лінію поведінки та уникнення ризику. Тому критерієм Вальда користуються у випадках, коли існує загроза дуже значних втрат в разі помилково прийнятого рішення; або якщо суб᾽єкт управління не схильний до ризику та прагне з більшою упевненістю отримати менший виграш замість значного, але непевного виграшу.

критерий крайнего пессимизма

7.2.2 Критерій максимакс (Критерий крайнего оптимизма)

Максимаксний критерій передбачає оптимістичну позицію щодо прийняття рішення та відповідає наступальній економічній стратегії. Цей критерій орієнтує суб᾽єкта управління на отримання максимально можливого результату рішення. Формалізований вираз цього критерію має вигляд:

(7.2)

Відповідно до цього критерію на основі даних матриці виграшів за кожним варіантом рішення визначають максимальне значення. Далі з-поміж обраних максимальних значень виграшу знаходять максимальну величину. Цій величині відповідатиме варіант рішення, що дозволить отримати найкращий економічний результат.

Платежная матрица		продали
		в1	в2	в3	в4	в5	Макс
произвели	а1	2	2	2	2	2	2
	а2	-0,2	2,4	2,4	2,4	2,4	2,4
	а3	-2,4	0,2	2,8	2,8	2,8	2,8
	а4	-4,6	-2	0,6	3,2	3,2	3,2
	а5	-6,8	-4,2	-1,6	1	3,6	3,6
	Max	2	2,4	2,8	3,2	3,6

Выбираем максимальные значения результата (максимальная прибыль или минимальный убыток) из всех вариантов производств – и из них выбираем максимальное значение – это и есть вариант производства.

Ответ: мы производим минимум – 18 булок - потому что в этом случае мы получим максимальную прибыль при самом хорошем варианте продаж.

Цей критерій передбачає ігнорування можливих несприятливих подій під час реалізації рішення, тому він придатний для ситуацій, коли суб᾽єкт управління є схильним до ризику, а можливі позитивні результати прийнятого рішення значно перевищують його можливі негативні наслідки.

7.2.3 Критерій Севіджа (минимального риска):

Мінімаксний критерій Севіджа використовується у випадках, коли потрібно за будь-яких умов уникнути великого ризику. Відповідно до цього критерію перевагу слід надати варіанту рішення, для якого максимальні втрати за різних варіантів стану економічного середовища виявляться мінімальними. Його формалізований вираз має вигляд:

(7.3)

де r_ij – втрати, що відповідають i-му рішенню при j-му варіанті стану економічного середовища.

Мы используем матрицу риска:

Матрица рисков		в1	в2	в3	в4	в5	Макс
	а1	0	0,4	0,8	1,2	1,6	1,6
	а2	2,2	0	0,4	0,8	1,2	2,2
	а3	4,4	2,2	0	0,4	0,8	4,4
	а4	6,6	4,4	2,2	0	0,4	6,6
	а5	8,8	6,6	4,4	2,2	0	8,8

При застосуванні критерію Севіджа вихідними даними є можливі втрати, що відповідають кожному зі сполучень варіантів рішень і стану економічного середовища, які отримують за даними матриці ризику. За кожним варіантом рішення знаходять величину максимально можливих втрат (збитків, недоотриманого прибутку). Серед отриманих максимальних значень знаходять мінімальне значення, яке відповідатиме оптимальному варіанту рішення за критерієм мінімаксу. Отже, у випадку реалізації цього варіанту рішення можливі втрати будуть мінімальними з усіх максимальних.

Даний критерій орієнтує суб᾽єкта управління на обережну лінію поведінки, орієнтовану на використання захисної стратегії та уникнення ризику. Використання цього критерію доцільне, якщо небезпека втрат дуже значна та необхідно забезпечити їх мінімізацію.

Спільною рисою критеріїв Вальда та Севіджа є орієнтація на обережну поведінку, пов᾽язану з уникненням ризику та песимістичною позицією щодо прийняття рішення. Але критерій Вальда орієнтований на отримання мінімального виграшу, а критерій Севіджа дозволяє мінімізувати можливі втрати [ивч, лагоша, гранат].

Недоліком критеріїв Вальда, максимакса та Севіджа є врахування тільки одного варіанту економічного середовища для кожного варіанта рішення [клим, с.87].

7.2.4 Критерій пессимизма–оптимизма Гурвіца

Критерій узагальненого максиміна (песимізму-оптимізму) Гурвіца використовується, якщо потрібно знайти певну комбінацію оптимістичної та песимістичної позицій щодо прийняття рішення. Відповідно до цього критерію перевагу надають варіанту рішення, для якого виконується умова:

, (7.4)

Коэффициент отображает меру пессимизма ЛПР

де χ – коефіцієнт, що відображає ступінь песимізму ЛПР ,

а_ij – виграш, що відповідає i-му рішенню при j-му варіанті стану економічного середовища.

Значення коефіцієнту песимізму встановлюються суб᾽єктивно, залежно від конкретних обставин та схильності до ризику особи, що приймає рішення. При χ = 0 має місце оптимістична позиція та орієнтація на граничний ризик, а величина критерію Гурвіца співпадає з величиною критерію максимакса. При χ = 1 суб᾽єкт управління налаштований песимістично та прагне уникати ризику, а величина критерію Гурвіца співпадає з величиною максимінного критерію Вальда. Значення χ між 0 і 1 є проміжними між ризиком і обережністю. Чим більша можлива небезпека, тим більш наближуватиметься до одиниці значення коефіцієнта песимізму. При зміні значення коефіцієнта песимізму змінюватиметься й варіант рішення, якому надається перевага. Отже, схильність до ризику суб᾽єкта управління значною мірою впливає на вибір рішення.

Визначити яку кількість продукції випускати компанією за допомогою критерію Гурвіца із коефіцієнтом оптимізму 0,7.

Соответственно коэффициент пессимизма = 0,3

Платежная матрица		продали							Х=
		в1	в2	в3	в4	в5	Макс	мин	0,3
произвели	а1	2	2	2	2	2	2	2	2
	а2	-0,2	2,4	2,4	2,4	2,4	2,4	-0,2	1,62
	а3	-2,4	0,2	2,8	2,8	2,8	2,8	-2,4	1,24
	а4	-4,6	-2	0,6	3,2	3,2	3,2	-4,6	0,86
	а5	-6,8	-4,2	-1,6	1	3,6	3,6	-6,8	0,48
	Max	2	2,4	2,8	3,2	3,6			2

Выбираем максимум и минимум по строкам.

По формуле – умножаем минимальное значение на критерий пессимизма, умножаем максимальное значение на критерий оптимизма (1 – критерий пессимизма = 0,7), потом складываем. Из полученных значений выбираем максимальное.

Розглянуті критерії пов᾽язані між собою, тому рекомендується використовувати їх комплексно. Остаточний вибір варіанта рішення слід здійснювати з урахуванням всіх розглянутих критеріїв.

Рассмотрим конкретный (сильно упрощенный) пример.

Пусть у некоего физического лица имеется 1000 долларов. Он предлагает рассмотреть 4 возможных стратегии:

положить деньги дома в шкаф;

положить деньги в банк на депозит (10% годовых);

вложить деньги в бизнес друга (рентабельность 100% в случае успеха);

купить лотерейные билеты (рентабельность 1000% в случае выигрыша).

Все возможные исходы предлагается получить исходя из следующего набора факторов:

уровень инфляции (%): 5, 10, 15;

судьба бизнеса: прогорел, не прогорел;

результаты лотереи: выиграл, не выиграл.

Период планирования — один год.

Предположим, что наш герой решил обратиться к консультанту за помощью в выборе наилучшей стратегии. Что же сделал консультант?

Прежде всего, он исключил из рассмотрения стратегию «лотерея». Потому что вероятность исхода «выиграл» существенно ниже всех остальных вероятностей (даже при том, что все они неизвестны)! Действительно, если бы вероятности были заданы, то эффективность стратегии («лотерея») была бы точно сильно ниже остальных. Это дает консультанту право исключить эту стратегию из рассмотрения. Вероятности всех остальных исходов для оставшихся стратегий, хоть и не известны, но сопоставимы. Поэтому все остальное консультант оставил.

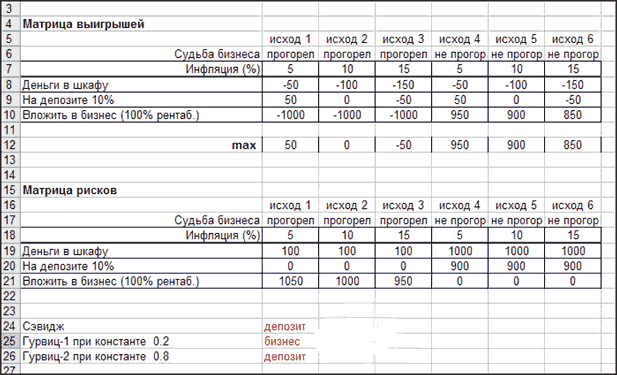
Далее консультант сформировал матрицу выигрышей и рассчитал на ее основе матрицу рисков (см. рисунок ниже).

После этого консультант применил рекомендации Сэвиджа и 2 раза Гурвица (с разными константами — уровнями оптимизма).

Сэвидж рекомендует депозит.

Гурвиц-1 (оптимист) — бизнес

Гурвиц-2 (пессимист) — депозит

Вывод — рекомендуется выбор стратегии «Депозит в банке».