Тема 7 – критерії прийняття рішень в умовах невизначеності.

7.1 Основні поняття теорії ігор, що застосовуються при обґрунтуванні рішень в умовах невизначеності. Матриця виграшів та матриця ризиків: сутність та порядок побудови.

7.2 Характеристика критеріїв прийняття рішень в умовах невизначеності.

7.2.1 Максимінний критерій Вальда.

7.2.2 Критерій максимакс.

7.2.3 Мінімаксний критерій Севіджа.

7.2.4 Критерій узагальненого оптимізму-песимізму Гурвіца.

7.1 Основні поняття теорії ігор, що застосовуються при обгрунтуванні рішень в умовах невизначеності

Невизначеність супроводжує процес прийняття та реалізації всіх господарських рішень. Дуже часто невизначеність обумовлена відсутністю достатньої інформації щодо умов прийняття рішень, які залежать від об᾽єктивної дійсності (природи). Тому виникає потреба у використанні спеціальних критеріїв, які дозволяють суб᾽єкту управління обрати оптимальне рішення з урахуванням невизначеності. Для цього можна скористатися основними положеннями теорії статистичних ігор.

Теорія ігор - теорія математичних моделей і методів, пов'язаних із прийняттям раціональних рішень в умовах конфлікту й невизначеності. Завданням теорії ігор є виявлення оптимальної стратегії (рішення) [сорока,132]. Якщо вивчаються ситуації протидії свідомого суб᾽єкта управління та економічного середовища (природи), яке не є свідомим, такі ситуації називаються іграми з природою (статистичними іграми), а розділ теорії ігор, який вивчає ігри з природою, називається теорією статистичних рішень [].

Відповідно до концепції теорії ігор суб᾽єкт управління зацікавлений у виборі оптимального варіанту рішення (стратегії), що забезпечує йому максимальний виграш або мінімальний програш.

В теории игр и теории решений применяются Матрицы игр. Это таблица, в которую заносятся возможные результаты принимаемых решений (например, исходы игры в случае выбора игроками той или иной стратегии).

Классический пример теории игр, называемый дилем­мой заключенных, иллюстрирует проблему, с которой сталкиваются олигопольные фирмы. Он заключается в сле­дующем: двух заключенных обвинили в совместном совер­шении преступления. Они находятся в отдельных тюрем­ных камерах и не могут поддерживать связь друг с другом. Каждого просили признаться в совершении прес­тупления. Если оба заключенных сознаются, каждый по­лучит срок заключения в 5 лет. Если никто не признается, судебное преследование будет трудно довести до конца, и поэтому заключенные могут получить двухгодичный срок наказания. С другой стороны, если один заключенный сознается, а другой нет, тот, кто признается, получит один год заключения, а другой сядет в тюрьму на де­сять лет. Если бы вы были одним из заключенных, сознались бы вы или нет?

	Заключенный В Признался	Заключенный В Не признался
Заключенный А Признался	__ 5 __ 5	— 1, — 10
Заключенный А Не признался	— 10, — 1	-2, -2

В дилемме заключённого предательство строго доминирует над сотрудничеством, поэтому единственное возможное равновесие — предательство обоих участников. Проще говоря, неважно, что сделает другой игрок, каждый выиграет больше, если предаст. Поскольку в любой ситуации предать выгоднее, чем сотрудничать, все рациональные игроки выберут предательство.

Ведя себя по отдельности рационально, вместе участники приходят к нерациональному решению: если оба предадут, они получат в сумме меньший выигрыш, чем если бы сотрудничали. В этом и заключается дилемма.

Олигополисты! Конкуренты при установлении цены!

Економічне середовище – сукупність невизначених чинників, у т.ч. й економічних, які впливають на ефективність рішення, що приймається. Наприклад, як складові економічного середовища можуть розглядатися попит на продукцію підприємства, рівень інфляції та ін. Отже, результати рішень, що приймаються, залежать від невідомої заздалегідь об᾽єктивної реальності.

У дискретному випадку економічне середовище являє собою повну групу взаємовиключних та взаємодоповнюючих подій. Тому сума ймовірностей станів економічного середовища дорівнює одиниці.

Ситуація прийняття рішень в умовах невизначеності характеризується множиною рішень (стратегій) суб'єкта управління (), множиною станів (стратегій) економічного середовища () та функціоналом оцінювання (Ѳ), визначеним на множині*, а також функцією- функцією виграшу суб'єкта управління [витл,184].

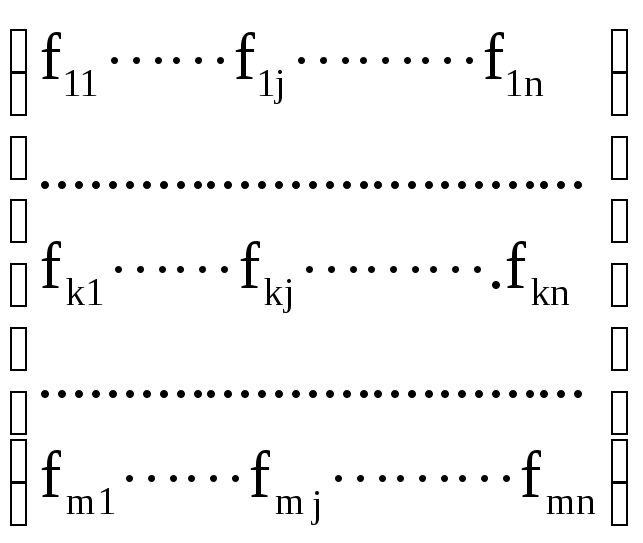
Якщо дискретною є множина стратегій (варіантів рішення) суб'єкта управління і множина станів економічного середовищаѲ₁, Ѳ₂, …. Ѳ_n, функціонал оцінювання задається матрицею:

	…....	Ѳ1 Ѳj Ѳn

елементи f_kj якої – це кількісна оцінка рішення за умови, що середовище знаходиться в стані Ѳ.

Рішенню відповідає вектор оцінювання, де k=1,……m.

Функціонал оцінювання може мати форму матриці виграшів (матриці ефективності рішень, що приймаються) або матриці ризиків (матриці втрат).

Матриця придатна для ситуації, коли:

• існує кінцева кількість розглянутих альтернатив дій і станів навколишнього середовища;

• має місце функція результатів, яка зараховує кожній альтернативі однозначний ефект у формі, наприклад, вартості капіталу, доходів, прибутків тощо;

• вартість капіталу чи отриманий прибуток (зазнаний збиток) буде єдино важливою цільовою величиною.

Матриця виграшів відображає можливі значення прибутку (доходу) або збитків як виграшів зі знаком «мінус» при різних сполученнях варіантів прийняття рішень та економічного середовища.

Для прийняття рішень в умовах невизначеності та ризику за допомогою статичної ігрової моделі вхідна інформація подається у вигляді матриці, рядки якої — це можливі альтернативні рішення, а стовпчики — стани системи (середовища).

У загальному вигляді матриця виграшів може бути представлена наступним чином (таблиця 7.1).

Таблиця 7.1 – Матриця виграшів

Варіанти рішення	Умови економічного середовища
	Ѳ1	Ѳ2	…....	Ѳn
х1	а11	а12	……	а1n
х2	а21	а22	……	а2n
….	……	……	……	……
xm	аm1	аm2	……	аmn

де х_m – варіанти рішення, що приймається;

Ѳ_n – варіанти економічного середовища;

а_mn – значення виграшів при різних варіантах рішення та станах економічного середовища.

Матриця ризику відображає суми прямих збитків або недоотриманого прибутку при різних варіантах прийняття рішень. Значення елементів матриці ризику визначаються як різниця між максимальним виграшем та виграшем по конкретному варіанту рішення при даному варіанті економічного середовища.

Матриця виграшів і матриця ризику містять вихідні дані, на основі яких за допомогою низки спеціальних критеріїв можливо розробити рекомендації щодо вибору та реалізації конкретних варіантів рішень. Завдання полягає в тому, що необхідно знайти такий варіант рішення, який в порівнянні з іншими є найбільш вигідним (доцільним).

Пример:

Варіант А.

Пекарня випікає хліб на продаж до магазинів. Собівартість однієї булки становить 0,90 грн. Її продають за 1,10 грн. У таблиці 3 приведений попит за останні 50 діб.

Таблиця 3