Размещения.

1) Размещения без повторений.

Определение 2: Пусть имеется различных предметов. Расстановки изэлементов поэлементов () называютсяразмещениями без повторений. Обозначают: . Здесь имеется в виду, что элементы в расстановках не повторяются.

В данном определении существенной является следующая позиция: две расстановки различны, если они отличаются хотя бы одним элементом или порядком элементов.

Теорема 1: Число всех размещений без повторений вычисляется по формуле:

.

Пример: Собрание из 25 человек выбирает президиум из 3 человек. Сколько возможно вариантов выбора?

.

Замечание: Число размещений без повторений можно также находить по формуле:

.

Если в знаменателе дроби , то принято считать.

2) Размещения с повторениями.

Определение размещений с повторениями аналогично предыдущему, но отличается существенно тем, что элементы в подмножествах могут повторяться. Обозначают: .

Теорема 2: Число всех размещений из элементов поэлементов с повторениями находится по формуле:

.

Доказать теорему можно индукцией по числу .

Примеры: количество телефонных номеров, автомобильных номеров, комбинаций в секретном замке, генетический код. Во всех этих ситуациях в расстановках элементы могут повторяться.

Количество комбинаций в секретном замке, число телефонных номеров, число автомобильных номеров, код Морзе, генетический код.

Разгадка генетического кода – крупнейшее достижение биологии ХХ века. Информация записана в гигантских молекулах ДНК (дезоксирибонуклеиновой кислоты). Различные молекулы ДНК отличаются порядком 4-х азотистых оснований. Эти основания определяют порядок построения белков организма из двух десятков аминокислот, причём каждая аминокислота зафиксирована кодом из 3-х азотистых оснований.

В одной хромосоме содержится несколько десятков миллионов азотистых оснований. Число различных комбинаций, в которых они могут идти друг за другом столь велико, что ничтожной доли этих комбинаций хватит для зашифровки всего многообразия живых организмов за время существования жизни на земле, оно равно , где– число оснований в хромосоме.

Перестановки.

1) Перестановки без повторений.

Определение 3: Пусть - конечное множество изэлементов.Перестановками из элементов множестваназываются все размещения изэлементов множества. Обозначается:.

Согласно определению:

.

Таким образом: .

2) Перестановки с повторениями.

Перестановки с повторениями используются в тех задачах, в которых речь идёт не о единичных объектах, а о видах, классах, сортах элементов. Понятно, что внутри каждого вида элементы повторяются.

Пусть имеются предметы различных типов:

.

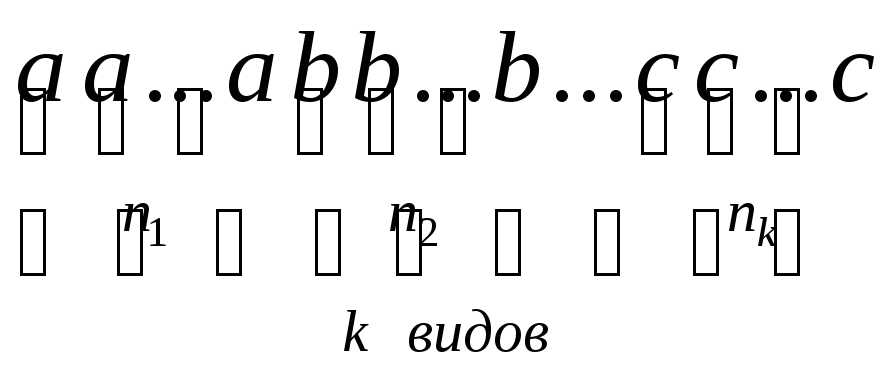Сколькими способами можно переставить местами элемент первого вида,элементов второго вида, ...,элементов последнего вида?

Число элементов в каждой перестановке равно: .

Перестановки элементов внутри вида не меняет перестановку. Она изменится только в случае межвидовых перестановок. Если бы все элементы были бы различными, то число всех перестановок равнялось бы . Но в силу того, что есть повторяющиеся объекты, получится меньшее число перестановок.

Теорема 3: Число различных перестановок с повторениями находится по формуле:

, где.

Замечание: В комбинаторике если не нужно засчитывать какое-то число способов, то на это число делят.

Поэтому в знаменателе дроби стоят числа (число перестановок элементов первого вида, которые не нужно засчитывать),(число перестановок элементов второго вида) и т. д. Перестановки элементов первого типа, второго типа и т.д. можно делать независимо друг от друга, поэтому по правилу умножения элементы данной перестановки можно переставлятьспособами. Значит, число различных перестановок с повторениями будет равно указанному числу.

Например, перестановки букв в словах мама, математика, анаграммы – есть перестановки с повторениями.