
- •Курс лекций
- •По дискретной математике
- •(2 Семестр)
- •(Для студентов специальности «Прикладная математика», «Компьютерные системы и сети»)
- •Комбинаторика.
- •§1. Правила комбинаторики. Основные комбинаторные формулы.
- •Размещения.
- •Перестановки.
- •Сочетания.
- •§2. Свойства сочетаний. Бином Ньютона.
- •§3. Числа Фибоначчи. Рекуррентные соотношения.
- •§3. Производящие функции.
- •Теория графов. Введение
- •§1. Основные понятия и определения теории графов.
- •§2. Задачи, послужившие основой теории графов.
- •1. Задача о кенигсбергских мостах.
- •2. Задача о четырех красках.
- •§3. Алгоритмические задачи.
- •1. Задачи о кратчайших путях.
- •Алгоритм решения.
- •Обоснование алгоритма.
- •2. Алгоритм построения Эйлерова цикла.
- •Обоснование алгоритма.
- •3. Потоки на транспортных сетях.
- •Алгоритм Форда - Фалкерсона для нахождения потока наибольшей величины.
- •Обоснование алгоритма.
- •§4. Цикломатическое число графа. Деревья.
- •§5. Эйлерова характеристика. Плоские графы.
- •§6. Теорема о пяти красках.
- •Оценка хроматического числа плоского графа.
- •§7. Графы правильных многогранников.
- •Теория конечных автоматов Введение.
- •§1. Определение автомата Мили. Автомат Мура.
- •§2. Покрытие и эквивалентность. Морфизмы.
- •§3. Эквивалентные состояния автоматов.
- •§4. Процедура минимизации конечных автоматов.
- •§5. Машина Тьюринга.
- •§6. Не полностью описанные автоматы.
- •Алгоритмы и рекурсивные функции. Введение.
- •§1. Основные понятия и определения.
- •§2. Примитивно рекурсивные функции.
- •§3. Частично рекурсивные функции.
- •§4. Машины Тьюринга.
- •Список литературы.
- •2 Семестр
§4. Процедура минимизации конечных автоматов.
Актуальность проблемы минимизации конечных автоматов уже была приведена выше. В реальном устройстве (калькулятор, компьютер) увеличение числа внутренних состояний ведёт к увеличению числа микросхем, что в свою очередь может привести к росту стоимости, к более частым поломкам. Значит, уменьшение числа внутренних состояний автомата без ограничения его возможностей ведёт к экономии и надёжности в работе.
Процедура минимизации основана на рассмотрении отношений эквивалентности между упорядоченными парами. Рассмотрим автомат, заданный таблицей внутренних состояний:
|
|
Следующее сост.
|
Выход
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Процедуру
минимизации начнем с нахождения множества
пар эквивалентных состояний
![]() и
и![]() .
Введем в рассмотрение разбиение
.
Введем в рассмотрение разбиение![]() ,
которое разобьет все состояния в таблице
на два класса эквивалентности:
,
которое разобьет все состояния в таблице
на два класса эквивалентности:
![]() ,
,![]() .
.
В
записи классов эквивалентности для
краткости мы пишем 1
вместо S1
и т.д. При составлении этого предварительного
разбиения мы ориентируемся на выходную
последовательность. Это разбиение
определяет график
![]() соответствующего отношения эквивалентности.
Т.к. отношение
соответствующего отношения эквивалентности.
Т.к. отношение
![]() рефлексивно и симметрично, то его график
легко восстанавливается по множеству
тех пар
рефлексивно и симметрично, то его график
легко восстанавливается по множеству
тех пар![]() ,
для которых
,
для которых![]() при всех значений входного символа
при всех значений входного символа![]() .
.
Обозначим
через
![]() подмножество, состоящее из пар
подмножество, состоящее из пар![]() ,
удовлетворяющих условию:
,
удовлетворяющих условию:![]() ,
для которых
,
для которых![]() .
В общем случае через
.
В общем случае через![]() будем обозначать множество упорядоченных
пар
будем обозначать множество упорядоченных
пар![]() со свойством
со свойством![]() .
Для нашего разбиения имеем:
.
Для нашего разбиения имеем:
![]() ,
,
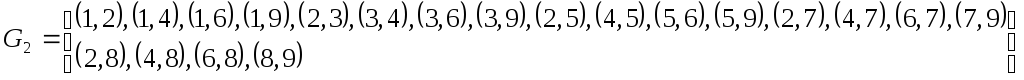
Т.к.
![]() и
и![]() - это классы эквивалентности относительно
- это классы эквивалентности относительно![]() ,
то имеем следующие соотношения:
,
то имеем следующие соотношения:![]() ,
,![]() ,
,![]() ,
,![]() и т.д.
и т.д.
Множество
![]() состоит из элементов множества
состоит из элементов множества![]() и еще пар
и еще пар![]() ,
,![]() и
и![]() .
Например, входной символ
.
Например, входной символ![]() переводит пару
переводит пару![]() в пару
в пару![]() ,
а эта последняя пара принадлежит
,
а эта последняя пара принадлежит![]() .
Добавление этихпар
к
.
Добавление этихпар
к
![]() определяет новое разбиение
определяет новое разбиение
![]() на классы эквивалентности:
на классы эквивалентности:
![]() :
: ![]() ,
,![]() ,
,![]() .
.
Определим
теперь множество
![]() .
Оно состоит из элементов множества
.
Оно состоит из элементов множества
![]() и еще пар
и еще пар
![]() и
и![]() .
Например, входной символ
.
Например, входной символ![]() переводит пару
переводит пару![]() в пару
в пару![]() ,
а эта последняя пара принадлежит
множеству
,
а эта последняя пара принадлежит
множеству
![]() .
.
При
разбиении
![]() имеем следующие классы эквивалентности:
имеем следующие классы эквивалентности:
![]() ,
, ![]() ,
,![]() ,
,![]() .
.
Множество
![]() состоит из элементов множества
состоит из элементов множества![]() и из пар
и из пар![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
Поэтому разбиение
.
Поэтому разбиение![]() состоит из следующих классов
эквивалентности:
состоит из следующих классов
эквивалентности:
![]() ,
, ![]() ,
,![]() ,
,![]() ,
,![]() .
.
Дальнейший
перебор показывает, что
![]() и
и![]() .
.
Конструкция
покрывающего автомата теперь несложна.
Каждый класс эквивалентности последнего
разбиения становится состоянием нового
автомата. Можно ввести новые обозначения.
Например,
![]() обозначим через
обозначим через![]() ,
,![]() - через
- через![]() и т.д. В итоге получается автомат с пятью
состояниями, покрывающий наш первоначальный
автомат с девятью состояниями. Поскольку
выходы для каждого начального состояния
в фиксированном классе эквивалентности
не зависят от этого состояния при
односимвольных входах, то таблица
состояний нового автомата, в частности
ее выходы, прямо считываются с таблицы
состояний первоначального автомата.
и т.д. В итоге получается автомат с пятью
состояниями, покрывающий наш первоначальный
автомат с девятью состояниями. Поскольку
выходы для каждого начального состояния
в фиксированном классе эквивалентности
не зависят от этого состояния при
односимвольных входах, то таблица
состояний нового автомата, в частности
ее выходы, прямо считываются с таблицы
состояний первоначального автомата.
Чтобы
построить функцию перехода в следующее
состояние, выберем то состояние
![]() в каждом классе
в каждом классе![]() ,
в котором некоторый элемент
,
в котором некоторый элемент![]() входной последовательности переводит
состояние
входной последовательности переводит
состояние![]() в некоторое состояние из класса
в некоторое состояние из класса![]() .
Положим
.
Положим![]() .
Заметим, что это предписание однозначно
определено: все состояния
.
Заметим, что это предписание однозначно
определено: все состояния![]() переходят в состояние
переходят в состояние![]() после считывания символа из входной
последовательности
после считывания символа из входной
последовательности![]() .
.
На следующем примере показан результат этой процедуры, примененной к автомату, рассмотренному раньше.
|
|
Следующее сост.
|
Выход
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Этот автомат уже является минимальным. Это значит, что он не содержит эквивалентных состояний.
Замечание:
На практике не обязательно перечислять
все пары из множеств
![]() и
и![]() .
На каждом шаге процедуры достаточно
смотреть, переводит ли некоторый входной
символ
.
На каждом шаге процедуры достаточно
смотреть, переводит ли некоторый входной
символ![]() пару
пару![]() из класса
из класса![]() в разные классы эквивалентности
в разные классы эквивалентности![]() и
и![]() .
Если да, то на следующем шаге состояния
.
Если да, то на следующем шаге состояния![]() и
и![]() следует развести по разным классам.
следует развести по разным классам.
Пример. Рассмотрим конечный автомат с пятью состояниями, заданный таблицей.
|
|
Следующее сост.
|
Выход
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Имеем
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Это приводит к разбиению
.
Это приводит к разбиению
![]() :
:
![]() ,
,![]() .
Тогда функция перехода при считывании
единицы имеет вид
.
Тогда функция перехода при считывании
единицы имеет вид![]() ,
кроме того
,
кроме того![]() .
Однако
.
Однако
![]() ,поэтому
,поэтому
![]() (т.к.
(т.к.
![]() и
и
![]() ).
).
Следующее разбиение состоит из классов эквивалентности:
![]() ,
,![]() ,
,![]() .
.
Дальнейшего
измельчения не происходит, т. к. функция
![]() переводит каждый элемент класса
эквивалентности в тот же класс. Итак,
состояния
переводит каждый элемент класса
эквивалентности в тот же класс. Итак,
состояния![]() и
и![]() можно склеить в одно состояние
можно склеить в одно состояние![]() ,
а состояния
,
а состояния![]() и
и![]() - в состояние
- в состояние![]() .
Состояние
.
Состояние![]() обозначаемтеперь
обозначаемтеперь
![]() .
Новый минимальный автомат, покрывающий
предыдущий, можно изобразить в виде:
.
Новый минимальный автомат, покрывающий
предыдущий, можно изобразить в виде:
|
|
Следующее сост.
|
Выход
|
|
|
|
|
|
|
|
|
|
|
|
|
