
- •Курс лекций
- •По дискретной математике
- •(2 Семестр)
- •(Для студентов специальности «Прикладная математика», «Компьютерные системы и сети»)
- •Комбинаторика.
- •§1. Правила комбинаторики. Основные комбинаторные формулы.
- •Размещения.
- •Перестановки.
- •Сочетания.
- •§2. Свойства сочетаний. Бином Ньютона.
- •§3. Числа Фибоначчи. Рекуррентные соотношения.
- •§3. Производящие функции.
- •Теория графов. Введение
- •§1. Основные понятия и определения теории графов.
- •§2. Задачи, послужившие основой теории графов.
- •1. Задача о кенигсбергских мостах.
- •2. Задача о четырех красках.
- •§3. Алгоритмические задачи.
- •1. Задачи о кратчайших путях.
- •Алгоритм решения.
- •Обоснование алгоритма.
- •2. Алгоритм построения Эйлерова цикла.
- •Обоснование алгоритма.
- •3. Потоки на транспортных сетях.
- •Алгоритм Форда - Фалкерсона для нахождения потока наибольшей величины.
- •Обоснование алгоритма.
- •§4. Цикломатическое число графа. Деревья.
- •§5. Эйлерова характеристика. Плоские графы.
- •§6. Теорема о пяти красках.
- •Оценка хроматического числа плоского графа.
- •§7. Графы правильных многогранников.
- •Теория конечных автоматов Введение.
- •§1. Определение автомата Мили. Автомат Мура.
- •§2. Покрытие и эквивалентность. Морфизмы.
- •§3. Эквивалентные состояния автоматов.
- •§4. Процедура минимизации конечных автоматов.
- •§5. Машина Тьюринга.
- •§6. Не полностью описанные автоматы.
- •Алгоритмы и рекурсивные функции. Введение.
- •§1. Основные понятия и определения.
- •§2. Примитивно рекурсивные функции.
- •§3. Частично рекурсивные функции.
- •§4. Машины Тьюринга.
- •Список литературы.
- •2 Семестр
§2. Покрытие и эквивалентность. Морфизмы.
Пусть
![]() - конечный автомат. Тогда по любой входной
строке
- конечный автомат. Тогда по любой входной
строке![]() длиныr
и по любому начальному состоянию
длиныr
и по любому начальному состоянию
![]() однозначно определяется строка длиныr
внутренних состояний
однозначно определяется строка длиныr
внутренних состояний
![]() ,
которая получается последовательным
применением отображения
,
которая получается последовательным
применением отображения![]() .
Точнее:
.
Точнее:![]() .
Аналогично строка на выходе определяется
последовательным применением отображения
.
Аналогично строка на выходе определяется
последовательным применением отображения![]() .
Поэтому рассмотрим автомат как устройство,
перерабатывающее пары, состоящие из
состояния
.
Поэтому рассмотрим автомат как устройство,
перерабатывающее пары, состоящие из
состояния![]() и
и![]() в строки
в строки![]() и
и![]() .
С помощью функций
.
С помощью функций![]() и
и![]() можно определить функции
можно определить функции![]() ,
,![]() ,
которые строятся по функциям
,
которые строятся по функциям![]() и
и![]() ,
заданным в описании автоматаМ.
,
заданным в описании автоматаМ.
Пример. Автомат задан диаграммой:
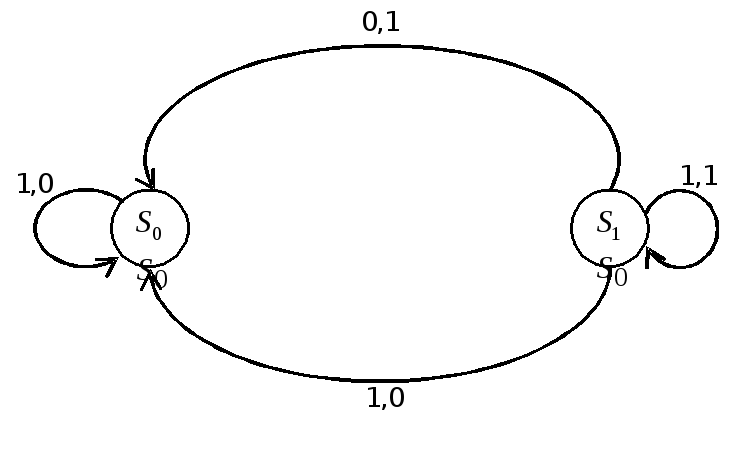
Пусть
входная строка
![]() и начальное состояние
и начальное состояние![]() ,
тогда
,
тогда![]() ,
,
![]() .
.
Увеличение числа внутренних состояний автомата в реальном устройстве приводит к росту количества электронных схем, к уменьшению надежности, к усложнению отладки и т. д. Поэтому число необходимых состояний автомата, предназначенного для выполнения определенных действий, стремятся уменьшить, не ограничивая его возможностей.
Этим
объясняется важность следующей задачи.
Предположим, что входной и выходной
алфавиты фиксированы. Возникает следующий
вопрос. Можно ли заменить автомат
![]() автоматом с меньшим числом внутренних
состояний
автоматом с меньшим числом внутренних
состояний![]() ,
но с той же функцией, переводящей входы
в выходы?
,
но с той же функцией, переводящей входы
в выходы?
Определение
1: Говорят,
что автомат
![]() покрывает
автомат
покрывает
автомат
![]() ,
если входной и выходной алфавиты у них
общие и существует функция
,
если входной и выходной алфавиты у них
общие и существует функция![]() ,
такая что для любого положительного
числа
,
такая что для любого положительного
числа![]() имеет место условие:
имеет место условие:
![]()
![]() .
.
Определение
2: Автомат,
который нельзя покрыть меньшим автоматом,
называется минимальным.
Будем писать:
![]() ,
если
,
если![]() покрывает
покрывает![]() .
.
Теорема 1: Отношение покрытий рефлексивно и транзитивно.
Доказательство очевидно.
Определение
3: Автоматы
![]() и
и![]() называютсяэквивалентными,
если автомат
называютсяэквивалентными,
если автомат
![]() покрывает
покрывает![]() и автомат
и автомат![]() покрывает
покрывает![]() .
В этом случае пишут:
.
В этом случае пишут:![]() .
.
Это
означает, что кроме функции
![]() со свойством, указанным в предыдущем
определении, существует еще функция
со свойством, указанным в предыдущем
определении, существует еще функция![]() со следующим свойством:
со следующим свойством:![]() при
при![]() и
и![]() .
.
Следствие: Отношение эквивалентности автоматов рефлексивно, транзитивно и симметрично.
Пусть
![]() и
и![]() – автоматы с общими входными и выходными
алфавитами.
– автоматы с общими входными и выходными
алфавитами.
Определение
4: Морфизмом
называется такое отображение
![]() ,
что
,
что![]() и
и![]()
![]() и
и![]() .
Если
.
Если![]() сюрьективно, то морфизм называетсяэпиморфизмом.
Если
сюрьективно, то морфизм называетсяэпиморфизмом.
Если
![]() - биекция, то морфизм называетсяизоморфизмом.
- биекция, то морфизм называетсяизоморфизмом.
Теорема
2: Пусть
![]() эпиморфизм автомата
эпиморфизм автомата![]() на
на![]() .
Тогда для любой входной строки
.
Тогда для любой входной строки![]() и любого начального состояния
и любого начального состояния![]() входная строка
входная строка![]() автомата
автомата![]() совпадает с входной строкой автомата
совпадает с входной строкой автомата![]() ,
если начальное состояние
,
если начальное состояние![]() равно
равно![]() .
.
Доказательство:
Доказательство
можно провести индукцией по числу
![]() с индуктивным шагом:
с индуктивным шагом:
![]() ;
;
![]() .
.
Следствие:
Любой эпиморфизм
![]() определяет покрытие автомата
определяет покрытие автомата![]() автоматом
автоматом![]() .
Изоморфизм автоматов
.
Изоморфизм автоматов![]() и
и![]() с общим входным и выходным алфавитами
есть биекция
с общим входным и выходным алфавитами
есть биекция![]() ,
такая, что для всякого начального
состояния
,
такая, что для всякого начального
состояния![]() и
всякой входной строки
и
всякой входной строки
![]() автоматы
автоматы![]() и
и![]() выдают одну и ту же выходную строку,
проходя через соответствующие
промежуточные состояния.
выдают одну и ту же выходную строку,
проходя через соответствующие
промежуточные состояния.
Пример. Автоматы, представленные следующими ориентированными графами, изоморфны.
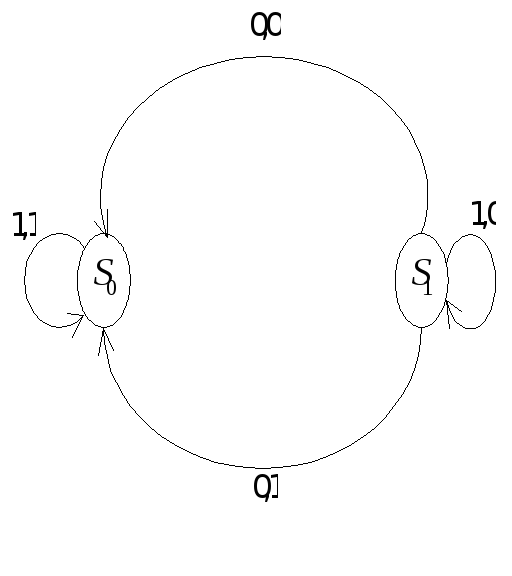
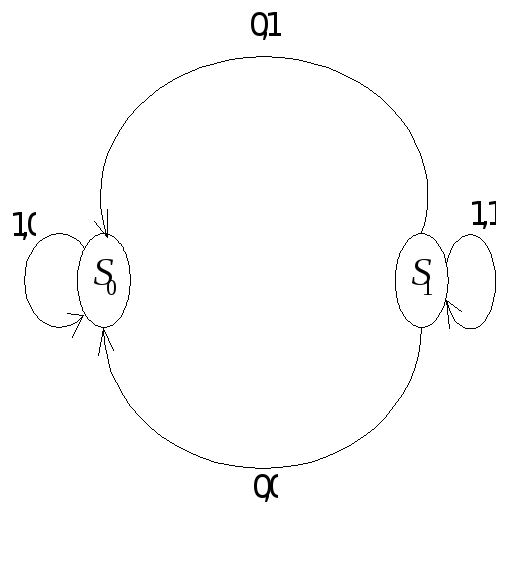
§3. Эквивалентные состояния автоматов.
В
этом параграфе мы решим следующую
задачу: по данному описанию автомата
![]() построить новый автомат
построить новый автомат![]() ,
который покрывает
,
который покрывает![]() (возможно, эквивалентен
(возможно, эквивалентен![]() )
и имеет наименьшее число состояний
среди всех автоматов, покрывающих
)
и имеет наименьшее число состояний
среди всех автоматов, покрывающих![]() .
.
Существует
эффективный метод решения этой задачи,
если функции
![]() всюду определены. Для этого сначала
определяют эквивалентные состояния
автомата, а затем склеивают все
эквивалентные состояния в одно.
всюду определены. Для этого сначала
определяют эквивалентные состояния
автомата, а затем склеивают все
эквивалентные состояния в одно.
Определение
1: Состояния
![]() и
и
![]() называются
называются![]() -эквивалентными,
если для всякой входной строки
-эквивалентными,
если для всякой входной строки
![]() длины
длины![]() имеем:
имеем:![]() .
В этом случае будем писать:
.
В этом случае будем писать:![]() .
Если
.
Если![]() ,
то будем говорить, что состояния
,
то будем говорить, что состояния
![]() и
и
![]() эквивалентны,
и писать:
эквивалентны,
и писать:
![]() .
.
Заметим,
что
![]() и
и![]() – действительно отношение эквивалентности.
Классы эквивалентности относительно
– действительно отношение эквивалентности.
Классы эквивалентности относительно![]() ,
являются множествами всех пар состояний,
перерабатывающих каждый входной символ
в фиксированный выходной символ
,
являются множествами всех пар состояний,
перерабатывающих каждый входной символ
в фиксированный выходной символ![]() .
Это означает, что
.
Это означает, что![]() .
Обозначим через
.
Обозначим через![]() отношения эквивалентности
отношения эквивалентности![]() (т.е. множество всех пар эквивалентных
состояний). Обозначим через
(т.е. множество всех пар эквивалентных
состояний). Обозначим через![]() дополнение к
дополнение к![]() ,
т.е.
,
т.е.![]() .
.
Пусть,
например, даны таблицы состояний
автоматов
![]() и
и![]() :
:
![]()
|
Текущее состояние |
ν 0 1 |
ξ 0 1 |
|
S0 S1 S2 |
S2 S1 S0 S2 S0 S1 |
0 1 1 0 0 1 |
![]()
|
Текущее состояние |
0 1 |
0 1 |
|
S0 S1 |
S0 S1 S0 S0 |
0 1 1 0 |
G (E1) = {(S0, S2), (S2, S0), (S0, S0), (S1, S1), (S2, S2)},
G (E1) = {(S0, S1), (S1, S0), (S1, S2), (S2, S1)}.
Задача минимизации количества состояний в полностью описанном автомате сводится к определению попарно эквивалентных состояний и последующему их склеиванию.
Оказывается,
что эффективнее всего начать с выявления
неэквивалентных состояний. Чтобы
показать это, определим новые функции
![]() и
и![]() .
.
Определение
2: Положим:
![]()
![]() .
Это означает, что
.
Это означает, что![]() есть последнее состояние автомата,
начавшего работу в состоянии
есть последнее состояние автомата,
начавшего работу в состоянии![]() ,
прочитавшего входную строку
,
прочитавшего входную строку![]() длины
длины![]() .
Положим далее:
.
Положим далее:![]()
![]() .
Это означает, что
.
Это означает, что![]() есть последний символ выходной строки
автомата, начавшего работать в состоянии
есть последний символ выходной строки
автомата, начавшего работать в состоянии![]() и считавшего ту же входную строку
и считавшего ту же входную строку![]() .
.
Теорема
1: Если
![]() ,
то либо
,
то либо![]() ,
либо для подходящей строки
,
либо для подходящей строки![]() имеем
имеем
![]() .
.
Доказательство:
Утверждение
![]() означает, что
означает, что![]() для подходящей строки
для подходящей строки![]() .
При необходимости мы можем укоротить
входную строку так, чтобы входные строки,
отвечающие
.
При необходимости мы можем укоротить
входную строку так, чтобы входные строки,
отвечающие![]() и
и![]() ,
отличались только последними символами.
Пусть это уже сделано. Если после этого
,
отличались только последними символами.
Пусть это уже сделано. Если после этого![]() ,
то
,
то![]() .
Если же
.
Если же![]() ,
то
,
то![]() .
Но
.
Но![]() при условии
при условии![]() .
Таким образом, последние выходные
символы автомата, считавшего
.
Таким образом, последние выходные
символы автомата, считавшего![]() ,
различны, если он исходил из начальных
состояний
,
различны, если он исходил из начальных
состояний![]() и
и![]() соответственно.
Чтобы выходы отличались, то есть
соответственно.
Чтобы выходы отличались, то есть![]() должно быть выполнено условие:
должно быть выполнено условие:![]() .
Иначе последний входной символ
.
Иначе последний входной символ![]() даст один и тот же символ на выходе.
даст один и тот же символ на выходе.
Теорема
2: Если
![]() ,
но
,
но![]() для всех
для всех![]() ,
то
,
то![]() для подходящего элемента
для подходящего элемента
![]() .
.
Эту
теорему можно переформулировать так:
если
![]() ,
то для подходящего элемента
,
то для подходящего элемента![]() имеем:
имеем:![]() .
Эта теорема утверждает, что состояния
.
Эта теорема утверждает, что состояния![]() и
и![]() ,
эквивалентные относительно всех входных
последовательностей длины
,
эквивалентные относительно всех входных
последовательностей длины![]() ,
могут стать неэквивалентными относительно
последовательностей длины
,
могут стать неэквивалентными относительно
последовательностей длины![]() только в том случае, когда имеется символ
только в том случае, когда имеется символ![]() ,
переводящий
,
переводящий![]() и
и![]() соответственно в состояния
соответственно в состояния![]() ,
не эквивалентные относительно подходящей
входной последовательности длины
,
не эквивалентные относительно подходящей
входной последовательности длины![]() .
Это означает, что на
.
Это означает, что на![]() шаге достаточно исследовать состояния
в
шаге достаточно исследовать состояния
в![]() и установить, найдется ли пара
и установить, найдется ли пара![]() ,
переходящая в пару
,
переходящая в пару![]() со свойством
со свойством![]() .
В этом случае
.
В этом случае![]() .
.
Если
мы уже определили
![]() ,
то
,
то![]() состоит из
состоит из![]() и таких упорядоченных пар
и таких упорядоченных пар![]() ,
что для некоторого
,
что для некоторого![]() имеем:
имеем:![]() .
В общем случае нужно исследовать каждый
раз только
.
В общем случае нужно исследовать каждый
раз только![]() .
Таким способом мы сумеем рекуррентно
определить
.
Таким способом мы сумеем рекуррентно
определить![]() и, наконец,
и, наконец,![]() - дополнение к
- дополнение к![]() в булевой алгебре подмножеств
в булевой алгебре подмножеств![]() .
.
Доказательство:
Доказательство теоремы проводится
непосредственно. Если пара
![]() лежит в
лежит в![]() ,
то она лежит в
,
то она лежит в![]() .
Значит нужно рассмотреть лишь такие
пары
.
Значит нужно рассмотреть лишь такие
пары![]() ,
что для некоторой строки
,
что для некоторой строки![]() имеем
имеем![]() ,
а для всех строк
,
а для всех строк![]() имеем
имеем![]() .
Но в точности те пары, которые переводятся
в
.
Но в точности те пары, которые переводятся
в![]() ,
,![]() -м
входным символом
-м
входным символом![]() и стало быть, в
и стало быть, в![]() ,
некоторым символом
,
некоторым символом![]() .
.
Лемма:
Если
![]() ,
то
,
то![]() для всех
для всех![]() .
.
Действительно,
дальнейшие шаги не добавят новых пар
состояний, т.к. согласно теореме 2,
дополнение
![]() состоит из тех пар, которые переводятся
подходящим символом
состоит из тех пар, которые переводятся
подходящим символом![]() в дополнение
в дополнение![]() .
.
Пример: Пусть задана таблица состояний некоторого автомата.
|
Текущее состояние |
След. состояние 0 1 |
Выход 0 1 |
|
S1 |
S1 S2 |
1 0 |
|
S2 |
S1 S3 |
1 0 |
|
S3 |
S5 S1 |
1 0 |
|
S4 |
S4 S2 |
1 0 |
|
S5 |
S4 S3 |
1 1 |
Для
этого автомата
![]() .
.
Иными
словами:
![]() .
Первое разбиение на классы эквивалентности:
.
Первое разбиение на классы эквивалентности:![]() ,
,![]() .
Вход 0 переводит
.
Вход 0 переводит
![]() в состояние
в состояние
![]() ,
,
![]() в
в![]() :
:![]() ,
,![]() .
Поэтому вход01
дает Следующие результаты:
.
Поэтому вход01
дает Следующие результаты:
![]() и
и![]() .
.
Отсюда
![]() и
и
![]() .
Аналогично:
.
Аналогично:
![]() и
и
![]() ,
так что имеет место условие:
,
так что имеет место условие:
![]() .
.
Далее,
входной символ 1 переводит состояние
![]() в
в
![]() ,
а
,
а![]() переводит в состояние
переводит в состояние![]() .
Другими словами:
.
Другими словами:![]() и
и![]() .
Поэтому
.
Поэтому![]() ,
т.к.
,
т.к.![]() и
и![]() .
Аналогично:
.
Аналогично:
![]() ,
откуда следует:
,
откуда следует:
![]() .
.
Таким
образом,
![]() разбивает
разбивает![]() на классы эквивалентности:
на классы эквивалентности:
![]() ,
,![]() ,
,![]() ,
,![]() .
.
Дальнейший
перебор показывает, что
![]() .
Таким образом,
.
Таким образом,![]() и
и![]() ,
а остальные пары состояний неэквивалентны.
,
а остальные пары состояний неэквивалентны.
