§7. Мощность множества. Сравнение мощностей.

Пусть даны конечные множества и, число элементов которых равноисоответственно. В зависимости от величини, возможны следующие ситуации:

, ,.

Какое из этих соотношений имеет место, можно решить двумя способами. Можно пересчитать число элементов каждого из множеств и сравнить полученные числа. А можно сравнить два множества путем установления взаимно однозначного соответствия между их элементами.

Определение 1: Назовем два множества эквивалентными, если существует взаимно однозначное соответствие между их элементами.

Обозначают: . Определенное нами бинарное отношение эквивалентности между множествами обладает свойствами:

1) рефлексивность: ,

2) симметричность: из того, что следует, что,

3) транзитивность: если и, то, т.е. действительно являетсяэквивалентностью.

Таким образом, всевозможные множества распадаются на классы эквивалентных между собой множеств. В один класс эквивалентности попадают множества, состоящие из одного и того же числа элементов.

Поставим в соответствие каждому классу эквивалентных между собой множеств некоторый символ, который назовемкардинальным числом или мощностью любого из множеств данного класса.

Например, линейная функция устанавливает взаимно однозначное соответствие между точками интервалаи точками интерваладля любого. Функцияустанавливает взаимно однозначное соответствие между всеми точками интервалаи точками прямой линии.

Замечание: Понятие мощности для конечного множества совпадает с понятием числа элементов этого множества. Кардинальное число – это количество элементов во множестве.

Определение 2: Множества, обладающие одинаковой мощностью, называются равномощными (эквивалентными).

Два конечных множества будут равномощными, если в них содержится одинаковое число элементов. Если имеем дело с бесконечными множествами, то вопросы, связанные с мощностями, решаются путём установления соответствия между элементами этих множеств.

Возвращаясь, к примеру, можно отметить, что множество точек любого интервала и прямой – равномощны. Это означает, что на прямой и в интервале одинаковое количество точек. Кардинальное число для бесконечного множества – это число, обозначаемое специальным символом или буквой.

При сравнении мощностей бесконечных множеств удобно пользоваться следующими вспомогательными теоремами.

Теорема 1 (о мощности промежуточного множества): Пусть , причем, тогда.

Т.е. теорема утверждает, что, если мощности крайних множеств одинаковы, то и мощность среднего (промежуточного множества), будет такой же.

Доказательство: По условию теоремы, крайние множества равномощны, т. е. . Это значит, что можно установить взаимно однозначное соответствие между элементами этих множеств. Пусть при этом собственной частимножествабудет соответствовать собственная часть множества, которую назовем. Итак,, где. В свою очередь, множествубудет соответствовать множество, т.е., где. Продолжая этот процесс неограниченно, получим последовательность множеств:

,

таких, что ,,,...

Кроме того, имеют место следующие эквивалентности:

,

,

.

Обозначим через общую часть множеств. Представим теперь множестваив виде сумм попарно непересекающихся частей:

,

.

Эти части эквивалентны, так как слагаемые первой и второй строки либо совпадают, либо эквивалентны. Что и требовалось доказать.

Теорема 2 (Кантора-Бернштейна): Если каждое из двух данных множеств эквивалентно некоторой части другого множества, то данные множества эквивалентны.

Доказательство:Пусть даны два множества и, причёми. Частиипредполагаем собственными, т.к. иначе теорема очевидна. Поставим элементы множестваво взаимно однозначное соответствие элементам множестваи назовем, ту собственную часть множества, которая составлена из элементов, соответствующих элементам множества. Тогда, причем,, следовательно, используя свойство транзитивности отношения эквивалентности, имеем:. Согласно предыдущей теореме,, но, значит данные множества эквивалентны:. Теорема доказана.

Следствие: Таким образом, при сравнении двух бесконечных множеств возможны следующие случаи:

1) между элементами множеств можно установить взаимно однозначное соответствие, тогда данные множества равномощны;

2) между элементами множеств нельзя установить взаимно однозначное соответствие, но можно установить взаимно однозначное соответствие между элементами одного из них и собственной частью другого, тогда мощность одного множества больше мощности другого.

Далее рассмотрим наиболее распространенные виды множеств в зависимости от их мощности.

Теорема 3: Мощность множества всех подмножеств любого непустого множества больше, чем мощность данного множества.

Доказательство: Пусть дано непустое множество . Обозначим множество всех его подмножеств. Мы покажем, чтоне эквивалентнои что, кроме того,эквивалентно некоторой части множества. Будем считать, что во множество подмножестввместе с другими входят несобственные подмножества множества. Докажем неэквивалентность множестви. Доказательство проведём от противного. Предположим, что. Тогда каждому элементусоответствует некоторое подмножествотого же множества, являющегося элементом множества. В данной ситуации возможны два случая. Либо элементпринадлежит тому подмножеству, которому тот соответствует, либо нет. Разобьём в соответствии с этим все элементы множествана две категории: «включенные» элементы и «не включенные». Обе категории не пусты. Так, элемент множества, соответствующий всему множествукак подмножеству, является включенным, а элемент множества, соответствующий его пустому подмножеству – не включённым. Рассмотрим подмножествомножества, составленное из всех не включённых элементов. Пусть этому элементу множествасоответствует некоторый элемент. Тогда окажется, чтоне может быть ни включенным, ни не включенным элементом. В самом деле, если он включенный, то, что невозможно т.к.составлено из не включенных элементов. Если- не включённый элемент, то он должен принадлежать, где собраны не включенные элементы, но тогда он оказывается включенным. Значит, и этот случай невозможен. Пришли к противоречию, которое возникло из-за неверного допущения. Тем самым доказано, что множестваине эквивалентны.

Доказательство того, что , где- собственное подмножество множества, очень просто. Достаточно взять в качествевсе одноэлементные подмножества множестваи поставить каждому из них в соответствие тот же элемент, из которого это одноэлементное множество состоит. Теорема доказана.

Следствие: Из доказанной теоремы следует, что для каждого кардинального числа существует большее кардинальное число.

В последующих рассуждениях важное место занимает множество натуральных чисел.

Определение 3: Множество, эквивалентное множеству чисел натурального ряда, называется счетным.

Натуральный ряд чисел – это счётное множество. Все множества, равномощные множеству , имеют такую же мощность.

Теорема 4: Для того чтобы множество было счетным, необходимо и достаточно, чтобы его элементы можно было «перенумеровать», т.е. представить в форме последовательности:

. (1)

Доказательство: Если множество представлено в форме (1), то достаточно каждому элементупоставить в соответствие его индекс, чтобы получить взаимно однозначное соответствие между множествоми, так что- счётно.

Обратно, если - счётно, то существует взаимно однозначное соответствиемежду множествамии. Обозначимчерези получим представление в форме (1).

Теорема 5: Из всякого бесконечного множества всегда можно выделить счётное подмножество.

Доказательство: Пусть - бесконечное множество. Возьмем в этом множестве произвольный элемент. Т.к.бесконечно, то в нём есть и другие элементы. Можно выбрать элемент. По тем же соображениям множествоне пусто и в нём можно выбрать элемент. Ввиду бесконечности множестваэтот процесс можно продолжать неограниченно. В результате получили последовательность элементов:. Эта выбранная последовательность и образует счётное подмножество, т. к. все элементы в ней перенумерованы. Что и требовалось доказать.

Следствие: Таким образом, мощность счётного множества наименьшая из всех мощностей бесконечных множеств. Всем множествам, эквивалентным множеству , ставится в соответствие одно и то же кардинальное число.

Теорема 6: Всякое бесконечное подмножество счётного множества счётно.

Доказательство: Пусть - счетное множество, а- его бесконечное подмножество. Так как множество- счётно, то все его элементы можно перенумеровать, т. е. представить в виде последовательности:. Будем перебирать один за другим элементы множествав порядке возрастания их номеров. При этом нам будут встречаться элементы множества. Соотнося каждому элементу множестваномер «встречи» с ним, мы перенумеруем множество, причём, в силу бесконечности, на его нумерацию пойдут все натуральные числа.

Следствие: Если из счётного множества удалить конечное подмножество, то оставшееся множество будет счётным.

Перечислим ещё некоторые свойства счётных множеств.

Так как для любого натурального числа множество вида- счетно, тогда сумма конечного и счётного множества без их общих элементов является счётным множеством.

Сумма конечного или счетного числа попарно не пересекающихся счетных множеств есть счётное множество. Покажем схематически, как можно занумеровать полученную сумму для конечного числа слагаемых:, где множестваимеют следующий вид:

,

,

.

Расположим элементы данных множеств так, как показано на рисунке. Таким образом, натуральные номера присваиваются сначала первым элементам данных множеств, затем – вторым и т. д.

Далее рассмотрим сумму (объединение) счётного числа попарно не пересекающихся счётных множеств: .

Н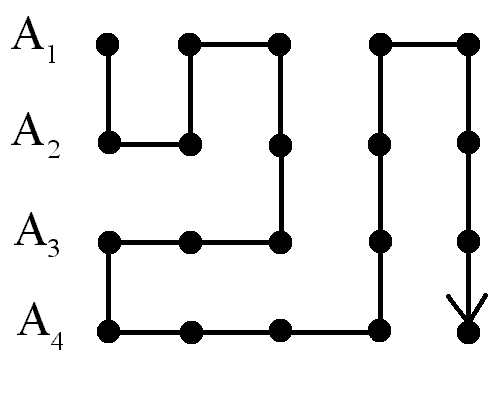а рисунке показана примерная схема нумерации элементов данных множеств. Пользуясь рассмотренными свойствами счётных множеств, можно всех целых чисел- счётно:

.

.

Это множество – есть объединение конечного числа счётных множеств, следовательно, оно является счётным.

Также схематически можно показать, что множество всех точек плоскости с целочисленными координатами счетно. Отсюда нетрудно вывести, что множество всех рациональных чисел также счетно.

Ниже рассмотрим множества, мощность которых отлична от мощности счётного множества.

Теорема 7: Множество всех последовательностей из нулей и единиц не счетно.

Доказательство: Рассматриваемое множество, очевидно, является бесконечным. Поэтому достаточно доказать, что не существует взаимно однозначного отображения множества натуральных чисел на множество двоичных последовательностей. Докажем это утверждение методом от противного. Предположим, что множество всех двоичных последовательностей можно перенумеровать, т.е. любой последовательности из нулей и единиц можно поставить в соответствие некоторый натуральный номер. Схематически это соответствие можно представить следующим образом:

,

,

,

. . . . . . . . . . . . . . . . . . . ,

,

. . . . . . . . . . . . . . . . . . . ,

Где - это элементы двоичных последовательностей, т. е. 0 или 1.

Покажем, что существует двоичная последовательность, которая при этом не получит номера. Построим такую последовательность следующим образом. Выберем первый её элемент(если, то; если, то). Аналогично выбираем остальные элементы:,,...,и т.д. Тем самым, для всех индексовбудет выбран элемент(если, то; если, то). Тогда построенная последовательностьне совпадает с первой последовательностью, так как. Она не совпадает со второй последовательностью, т.к.и т.д. Последовательностьне совпадает с последовательностью, получившей номер, т.к.и т.д. Таким образом, последовательностьне может получить номера вопреки предположению. Это означает, что множество всех двоичных последовательностей не эквивалентно множеству натуральных чисел. Тем самым доказано, что множество двоичных последовательностей нечетно.

Замечание: Метод доказательства, примененный в теореме 7, называют Канторовым диагональным методом. Его можно использовать при решении задач и при доказательстве подобных утверждений.

Применяя Канторов диагональный метод, можно, например, доказать, что множество всех точек отрезка несчетно.

Нетрудно показать, что мощность множества всех двоичных последовательностей равна мощности множества всех действительных чисел отрезка , или мощности всех последовательностей натуральных чисел. Все эти множества являются несчётными, а также равномощными, значит, им соответствует одно и то же кардинальное число.

Действительно, каждую цифру в десятичной записи числа или каждое натуральное число можно зашифровать конечным набором из 0 и 1, поэтому любое действительное число отрезка или любую последовательность натуральных чисел можно зашифровать последовательностью из нулей и единиц.

На протяжении трех лет (с 1871 по 1874г.) основатель теории множеств Георг Кантор искал доказательство того, что взаимно однозначное соответствие между точками отрезка и точками квадрата невозможно. Неожиданно ему удались построить соответствие, которое он считал невозможным! Математику Дедекинду он писал: «И вижу это, но не верю». Но интуиция подвела и здесь.

Дадим эскиз доказательства Кантора. Каждую точку квадрата можно задать её координатамии. Эти числа можно записать, как бесконечные десятичные дроби, т.к.и. не больше 1.

Пусть ,(для простоты мы взяли внутренние точки квадрата). Выпишем число, десятичные знаки которого получаются «перемешиванием» десятичных знаков чиселиследующим образом:.

Точка принадлежит отрезку, причем соответствиеявляется взаимно однозначным. Таким образом, установлено взаимно однозначное соответствие между всеми точками квадрата и частью точек отрезка. Это показывает, что множество, точек квадрата имеет не большую мощность, чем множества точек отрезка. Но его мощность и не меньшее, а потому эти мощности совпадают. Не только квадрат, но и куб, и вообще любая геометрическая фигура, содержащая хотя бы одну лини, имеет столько же точек и отрезок. Такие множества назовёммножествами мощности континуум (от латинского слова continuum - непрерывный).

Перечисленные выше множества точек отрезка , множество всех двоичных последовательностей и др. имеют мощность континуум. Можно показать, что множество всех подмножеств любого счетного множества имеет мощность континуум.

Возникает вопрос, существует ли множество, мощность которого больше мощности счетного множества и меньше, чем континуум. Эта задача получила название проблемы континуума. Над этой проблемой думали многие выдающиеся математики, начиная с Г. Кантора, но до 60-х годов XX века эта проблема оставалась нерешенной. В течение многих лет думал над этой проблемой один из крупнейших математиков Н.Н. Лузин. Правда, в ходе размышлений над проблемой континуума Н.Н Лузин решил целый ряд труднейших задач теории множеств и создал целый раздел математики - дескриптивную теорию множеств.

Неудачи попыток решить проблему континуума не были случайными. Оказалось, что положение дел здесь напоминает историю постулата параллельных прямых. Этот постулат пытались на протяжении двух тысячелетий вывести из остальных аксиом евклидовой геометрии. После работ Лобачевского, Гильберта и ряда других ученых выяснилось, что пятый постулат не противоречит остальным аксиомам, но и не может быть выведен из них. Точно так же после работ К. Гёделя, П. С. Новикова, Дж. Коэна и других выяснилось, что утверждение об отсутствии множества промежуточной мощности является аксиомой теории множеств. Не существует мощности, большей, чем мощность счётного множества, и меньшей мощности континуум. Если множество имеет мощность, большую мощности счётного множества, то данное множество имеет мощность континуум.