Представление бинарных отношений графами.

Понятие графа используется в математике для наглядного представления бинарных отношений, заданных на конечных множествах.

Граф представляет собой конечный набор точек плоскости (вершины графа). Часть вершин может быть соединена отрезками со стрелками или без них (дуги и рёбра). Фигура, состоящая из вершин и дуг (отрезки со стрелками), называется ориентированным графом. Фигура, состоящая из вершин и рёбер (без направлений), называется неориентированным графом. Пусть, например, даны конечные множества ,. Зададим на этих множествах бинарное отношение:.

a b

c

e d

f

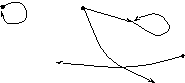
Полученная фигура называется графом отношения . Любое бинарное отношение, заданное на конечных множествах, может быть представлено в виде некоторого графа. Верно и обратное: всякий граф представляет собой некоторое бинарное отношение на тех конечных множествах, на которых определён граф.

Т.к. бинарные отношения между элементами множеств иявляются подмножествами, то можно говорить о включении одного бинарного отношения в другое, а также о пересечении и объединении бинарных отношений, или одополнении к бинарному отношению. Дополнение бинарного отношения определяют следующим образом: . Другими словами паратогда и только тогда, когда.

Если на множестве заданы произвольные бинарные отношенияи, то можно рассматривать произведение бинарных отношений, а так же единичное, нулевое и обратное бинарные отношения.

Определение 7: Произведение определим следующим образом: элементынаходятся в отношениитогда и только тогда, когда во множествесуществует хотя бы один такой элемент, чтои.

Произведение бинарных отношений обладает свойством ассоциативности, но не коммутативно.

Определение 8: Единичным бинарным отношением (или диагональю) называется бинарное отношение , такое, чтотогда и только тогда, когда. Другими словами единичное бинарное отношениезадается множеством всех пар,для всех.

Для любого бинарного отношения на множествеимеет место равенство: , т. е. коммутативность в этом случае выполняется.

Отметим, что пустое (нулевое) бинарное отношение играет роль нуля при умножении бинарных отношений. Для любого бинарного отношенияимеет место свойство:.

Для любого бинарного отношения ,обратное отношение определяется следующим образом: тогда и только тогда, когда. Очевидным является тот факт, что, а также.

Замечание: Понятие бинарного отношения допускает обобщения. Если на множестве задано одно или несколько- местных отношений, то такое множество называетсямоделью. Теория моделей – это один из разделов современной алгебры.

§4. Бинарные отношения эквивалентности и порядка. Фактор-множество.

В данном параграфе будут рассмотрены некоторые виды бинарных отношений. Рассмотрим непустое множество и зададим на нём бинарное отношение. Отношениеназываетсядиагональю множества и определяет отношение равенства элементов множества.

Определение 1: Бинарное отношение называетсярефлексивным, если для всякого элемента выполняется условие: , т. е. диагональ должна принадлежать отношению. Иначе можно записать:- элементнаходится в отношениис самим собой.

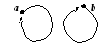
Граф рефлексивного бинарного отношения содержит петли около каждой своей вершины.

Определение 2: Бинарное отношение называетсяантирефлексивным, если для всякого элемента выполняется условие: .

Граф антирефлексивного отношения не должен иметь петель.

Определение 3: Бинарное отношение называетсясимметричным, если для произвольных элементов выполняется условие:, или иначе.

Каждая дуга симметричного графа обязательно имеет двойную стрелку (ребро). Если хотя бы для одной параусловие определения не выполняется, т. е., то отношение симметричным не является.

Определение 4: Бинарное отношение называетсяантисимметричным, если для произвольных элементов ивыполняется условие:

и, то.

Граф такого отношения имеет петли.

Определение 5: Бинарное отношение называетсятранзитивным, если для любых элементов выполняется следующее условие:

и, то.

Иначе можно написать:и, то. Читается: еслинаходится в отношениис, анаходится в отношениис, тонаходится в отношениис.

Определение 6: Бинарное отношение называетсясвязным, если для любых справедливо утверждение:

.

Приведём примеры. Пусть рассматривается множество натуральных чисел. Зададим бинарное отношениена декартовом квадрате этого множестваследующим образом:(элементнаходится в отношениис элементомтогда и только тогда, когдаделится на). Проверим свойства отношения делимости натуральных чисел.

1) - рефлексивность выполняется, т. к. любое число делится без остатка само на себя.

2) из того, что не следует, что- симметричность не выполняется (например,, но).

3) выполняется антисимметричность: если и, то.

4) выполняется транзитивность: если и, то.

5) связность не выполняется: если , то отсюда не следует, чтои.

Таким образом, отношение делимости, заданное на множестве натуральных чисел, рефлексивно, антисимметрично и транзитивно.

Определение 7: Бинарное отношение называетсяотношением эквивалентности, если оно рефлексивно, симметрично и транзитивно.

Примеры: 1) отношение равенства на любом числовом множестве является отношением эквивалентности, т. к. каковы бы ни были числа a, b, c имеют место следующие утверждения:

а) ; б); в).

2) отношение параллельности на множестве прямых плоскости – это отношение эквивалентности, так как для любых прямых справедливы следующие положения:

а) ||; б)||, то||; в)||и||, то||.

3) отношение подобия на множестве всех треугольников также является рефлексивным, симметричным и транзитивным, а значит, является отношением эквивалентности.

Определение 8: Пусть - непустое множество,- множество всех подмножеств множества. Пусть- некоторая система подмножеств множества, т. е.. Система подмножествназываетсяразбиением множества , если выполняются следующие условия:

1) среди множеств системы нет;

2) два различных множества из системы не пересекаются;

3) объединение всех множеств системы даёт множество.

Пример: Пусть , гдеиявляются числовыми промежутками:,. Тогда системаявляется разбиением для множествадействительных чисел, т. к. выполнены все требования определения.

Определение 9: Пусть ,- отношение эквивалентности на множестве,- произвольный элемент множества. Множествоназываетсяклассом эквивалентности, порожденным элементом .

Определение 10: Множество всех классов эквивалентности по отношению эквивалентности называетсяфактор-множеством множества по отношению. Обозначают:. Согласно определению:

.

Примеры:

1) Для примера рассмотрим отношение сравнения на множестве целых чисел . Целые числаиназываются сравнимыми по модулю, если их разность делится набез остатка. Обозначают:. Кратко это определение можно представить в виде:

.

Не сложно показать, что отношение сравнения является отношением эквивалентности, т. е. рефлексивно, симметрично и транзитивно. Найдём все классы эквивалентности и фактор-множество для случая .

а) рассмотрим элемент и. Класс эквивалентности, порождённый нулём, состоит из всех целых чисел, делящихся на 5 без остатка (0 – это остаток при делении на 5). Таким образом, имеем класс.

б) элемент порождает класс эквивалентности, состоящий из целых чисел, которые при делении на 5, дают в остатке 1. Имеем класс:.

в) аналогично рассуждая, получаем классы, порождённые элементами 2, 3, 4:

, ,.

г) Класс, порождённый элементом 5, совпадает с классом, порождённым нулём:

.

Все найденные классы эквивалентности образуют фактор-множество:

, где- отношение сравнения по модулю 5.

2) Подобные конструкции встречаются и в школьной математике чрезвычайно часто. Известно, например, что фигурой на плоскости называется некоторое множество точек плоскости. Введем во множестве всех плоских фигур отношение эквивалентности, считая две фигуры эквивалентными, если их можно совместить движением. Фактор-множество по этому отношению эквивалентности состоит из классов таких, что любые две фигуры одного класса можно совместить движением. Отождествляя все фигуры одного класса, мы говорим, например, о равенстве фигур.

Теорема 1: Пусть ,- отношение эквивалентности на множестве, тогда фактор-множествоявляется разбиением множества.

Доказательство: Для доказательства достаточно показать, что фактор-множество удовлетворяет всем условиям определения разбиения множества.

1) Множество состоит из классов эквивалентности. Пусть- некоторый элемент фактор-множества. По условию теоремы, отношение- рефлексивно, значит, следовательно.

2) Нужно показать, что два различных класса не пересекаются. Пусть - такие классы эквивалентности, что. Покажем, что классыине пересекаются. Допустим противное. Предположим, что, тогда найдётся элемент, который принадлежит этим двум классам:.

Пусть - произвольный элемент из класса, т. е.. Тогдаи. Отсюда в силу симметричности отношения:и. Тогда, в силу транзитивности отношения:. Применяем те же рассуждения:и. Значит,, т. к.- транзитивно. Из последней записи видно, что. Таким образом, доказано включение:. Рассуждая аналогично, можно показать, что. Следовательно,, а это противоречит тому, что. Противоречие возникло из неверного допущения:. Значит, доказано, что два различных класса не пересекаются.

3) Доказательство последнего пункта определения разбиения можно получить непосредственно из определения фактор-множества. Теорема доказана.

Определение 11: Пусть ,- разбиение множества. Определим отношениеследующим образом: Элементыпоставлены в отношениетолько в том случае, когда они принадлежат одному классу эквивалентности. Отношениеназываетсябинарным отношением, определённым разбиением .

Теорема 2: Пусть ,- разбиение множества,- бинарное отношение, определённое разбиением. Тогда- является отношением эквивалентности и фактор-множествосовпадает с разбиением.

Доказательство: По определению: . Тогда условие:

1) - выражает рефлексивность отношения.

2) - выражает симметричность отношения.

3) - транзитивность.

Следовательно, - есть отношение эквивалентности. Тогда, согласно теореме1, фактор-множество совпадает с разбиением. Теорема доказана.

Определение 12: Пусть ,- бинарное отношение, определённое на множестве. Отношениена множественазываетсяотношением порядка, если оно антисимметрично и транзитивно.

Определение 13: Порядок на множественазываетсястрогим, если бинарное отношение антирефлексивно. Порядокназываетсянестрогим, если рефлексивно.

Замечание: Бинарное отношение, обладающее свойствами рефлексивности, транзитивности и антисимметричности, также называют отношением частичного порядка. Множество с заданной на нем частичной упорядоченностью называетсячастично упорядоченным множеством.

Примеры:

1) Отношение < на множестве - это отношение строгого порядка (антисимметрично, антирефлексивно, транзитивно).

2) Отношение ≤ на множестве - это отношение нестрогого порядка (антисимметрично, рефлексивно, транзитивно).

3) Рассмотрим множество , пусть- множество всех подмножеств множества. Проверим свойства отношения включения. Пусть.

а) -рефлексивность;

б) если и, то-антисимметричность;

в) если и, то-транзитивность.

Значит, отношение включения – это отношение нестрогого порядка.

4) На множестве зададим отношениеследующим образом:

(читают:ниже, если- делитель).

Проверяя свойства этого отношения, легко можно убедиться, что оно является отношением нестрогого порядка.

Определение 14: Отношение порядка на множественазываетсялинейным (или отношением бинарного порядка), если бинарное отношение связно, т. е. для любых элементов: если, то.

Отношение частичного порядка не является линейным.

Примеры:

1) Отношение < на множестве - строгий линейный порядок.

2) Отношение ≤ на множестве натуральных чисел - это нестрогий линейный порядок.

3) Отношение на множестве- это нестрогий частичный порядок.

Определение 15: Пусть во множестве задана частичная упорядоченность (бинарное отношение ≤). Элементыиэтого множества называютсясравнимыми, если и.

Не всякие два элемента из множества могут быть сравнимыми, по этой причине мы говорим о «частичной» упорядоченности. Так, например, тривиальная частичная упорядоченность множествазадается диагональю, в этом случаетолько если, разные элементы из множествав этом случае будут несравнимыми.

Определение 16: Пусть - отношение порядка на множестве. Если- отношение частичного порядка и элементытакие, чтои,, тогда элементыиназываютсянесравнимыми элементами при заданном порядке .

Определение 17: Частично упорядоченное множество называетсялинейно упорядоченным или цепью, если любые два элемента этого множества сравнимы, т.е. для любых либо, либо.

Примеры:

1) Множество натуральных, целых, рациональных и действительных чисел в их естественной упорядоченности будут линейно упорядочен­ными множествами.

2) Множество всех подмножеств некоторого данного множества соотношением теоретико-множественного включения будет частично упорядоченным, но не линейно упорядоченным множеством.

Доказано, что всякое частичная упорядоченность может быть продолжена до линейной упорядоченности этого множества, т.е. может быть включена в линейную упорядоченность (в смысле включения бинарных отношений).