§4. Комбинаторика с повторениями.

Одна из особенностей комбинаторных задач заключается в том, что в ней исключительно большую роль играет точность формулировки. Обычно в задаче по комбинаторике необходимо определить количество способов или число вариантов какого-либо выбора. Варианты – это умозрительные понятия и их нельзя увидеть непосредственно, если нет полного перечня различных вариантов, описанных с помощью математических символов.

Рассмотрим для примера задачу: определить, сколькими способами можно распределить три конфеты между тремя детьми? Решение зависит от выбранного способа понимания задачи. Источником неопределенности является слово «распределить». Если считать конфеты одинаковыми, то справедливый вариант распределения дает 1 способ , т.е. каждый ребенок получил по одной конфете. Если же делить не поровну, то возможны варианты распределения:,,,,,,,,. Таким образом, «распределения» дают 10 различных вариантов. Если же дополнительно предположить, что все конфеты различные, то можно получить максимальное число «распределений» - 27 вариантов.

Таким образом, при решении задач важно точно понимать смысл слов «различные варианты». Нужно выяснить, важен ли порядок элементов в выбранном подмножестве, или важен только состав. Кроме того, важно понять, могут ли повторяться элементы, или они берутся в одном экземпляре. Комбинаторные формулы без повторений рассмотрены в §2. В данном параграфе будут рассмотрены формулы и задачи, в которых элементы множества при некотором выборе могут повторяться.

1) Перестановки с повторениями.

Пример 1. Сколькими способами можно переставить буквы в слове «мама»?

Решение. Комбинаторика позволяет считать словом любую комбинацию букв. Если бы в слове «мама» все буквы были бы различными, тогда количество перестановок было бы равно . Но при перестановке двух букв«м» или двух букв «а» будем получать одинаковые буквенные комбинации. Поэтому, их засчитывать не надо. Две буквы «м» можно переставить способами. Аналогично для букв«а». В итоге число перестановок букв данного слова без учета повторов окажется равным числу . При необходимости все способы можно перебрать.

Замечание. Обычно, если при решении задачи какие-либо варианты не нужно считать, то на это число делят. Этот подход является обратным к правилу умножения.

Перестановки с повторениями используются в тех задачах, в которых речь идёт не о единичных объектах, а о видах, классах, сортах элементов. Понятно, что внутри каждого вида элементы повторяются.

Пусть имеются предметы различных типов:

.

Сколькими способами можно переставить местами элемент первого вида,элементов второго вида, ...,элементов последнего вида?

Общее количество всех элементов в каждой перестановке равно: . Перестановки элементов внутри вида не меняет перестановку. Она изменится только в случае межвидовых перестановок. Будем рассуждать аналогично задаче в примере 1. Если бы все элементы были бы различными, то число всех перестановок равнялось бы. Но в силу того, что есть повторяющиеся объекты, получится меньшее число перестановок, потому что не нужно считать перестановки элементов первого вида, а их будет, не надо засчитыватьперестановок элементов внутри второго вида и т.д.

Таким образом, число различных перестановок с повторениями находится по формуле:

, где . (1)

В знаменателе дроби стоят числа (число перестановок элементов первого вида, которые не нужно засчитывать),(число перестановок элементов второго вида) и т. д. Перестановки элементов первого типа, второго типа и т.д. можно делать независимо друг от друга, поэтому по правилу умножения элементы данной перестановки можно переставлятьспособами. Значит, число различных перестановок с повторениями будет равно указанному числу.

Например, перестановки букв в слове «математика» – это перестановки с повторениями. Анаграммы – есть перестановки с повторениями.

Замечание. Дробь, стоящая в правой части формулы (1), является целым числом.

Пример 2. Найти количество анаграмм слова «баобаб».

Решение. Всего – 6 букв. Вхождения букв: «б» - 3 раза, «а» - 2 раза, «о» - 1 раз. Используя формулу (1), имеем:

.

Замечание. Формула для числа перестановок с повторением содержит в себе, как частный случай, формулу для перестановок без повторений (при ). Кроме того, формула (1) содержит в себе формулу для числа сочетаний (при):.

Действительно, если , то тогда,, …,,. Значит,, т.е. обычные перестановки без повторений – это частный случай перестановок с повторениями.

Если , то, или, тогда по определениюиимеем:

.

Таким образом, если положить , то последнее равенство примет более естественный для формулы числа сочетаний вид:

.

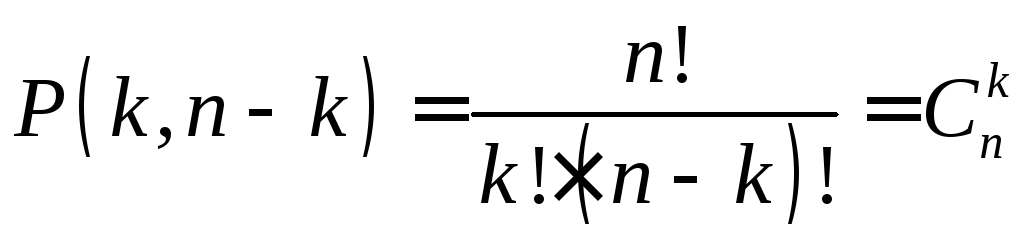2) Размещения с повторениями.

Определение размещений с повторениями аналогично определению числа размещений без повторений, но отличается существенно тем, что элементы в подмножествах могут повторяться.

Определение 1: Слова, составленные из букв, которые можно получить изповторяющихся букв, называютразмещениями с повторениями.

Обозначают: .

Теорема 1: Число всех размещений из элементов поэлементов с повторениями находится по формуле:

. (2)

Доказательство. Если имеется упорядоченных мест, для каждого из которых можно выбрать любой изобъектов, то согласно комбинаторному принципу умножения, существуетспособов выбора объектов. Таким образом, число перестановок с повторением, когдаобъектов выбираются изобъектов, равно, что и требовалось доказать.

Примеры. 1) Количество телефонных номеров, автомобильных номеров, комбинаций в секретном замке, генетический код. Во всех этих ситуациях в расстановках элементы могут повторяться. Количество комбинаций в секретном замке, число телефонных номеров, число автомобильных номеров, код Морзе, генетический код.

2) Разгадка генетического кода – крупнейшее достижение биологии ХХ века. Информация записана в гигантских молекулах ДНК (дезоксирибонуклеиновой кислоты). Различные молекулы ДНК отличаются порядком 4-х азотистых оснований. Эти основания определяют порядок построения белков организма из двух десятков аминокислот, причём каждая аминокислота зафиксирована кодом из 3-х азотистых оснований.

В одной хромосоме содержится несколько десятков миллионов азотистых оснований. Число различных комбинаций, в которых они могут идти друг за другом столь велико, что ничтожной доли этих комбинаций хватит для зашифровки всего многообразия живых организмов за время существования жизни на земле, оно равно , где– число оснований в хромосоме.

3) Пусть имеется множество . Требуется составить его двухэлементные подмножества.

Решение. Если считать, что в этих подмножествах важен только состав, то имеем 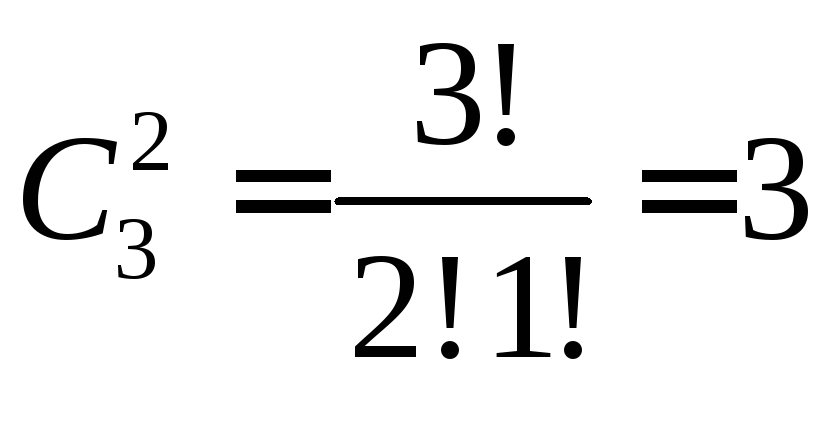таких подмножества:,,.

Если считать, что в подмножествах важен состав и порядок элементов, то имеем таких подмножеств:

, ,,,,.

В таких парах порядок элементов будет важен, если например, речь идет о координатах точек на плоскости.

Если же в построенных подмножествах элементы могут повторяться, то имеем таких подмножеств:

, ,,,,,,,.

Замечание. Выше было показано, что перестановки без повторений являются частным случаем размещений без повторений. Для формул с повторениями дело обстоит иначе. Формула числа перестановок с повторениями не является частным случаем формулы числа размещений с повторениями.

Действительно, когда речь идет о повторениях в упорядоченном или неупорядоченном наборе объектов, то возможны две противоположные ситуации:

1) каждый объект должен повторяться в наборе строго заданное число раз;

2) нет никаких ограничений на число повторений объектов, кроме общего их числа в наборе.

В этом отличие перестановок с повторениями и размещений с повторениями. Объединяет их другое – это упорядоченные наборы. Отметим, что для неупорядоченных наборов ситуация с фиксированным набором каждого объекта бессодержательна, поскольку в таком случае это один вариант.

Размещение с повторениями – термин достаточно явный и удобный. В случае «сочетаний с повторениями» с ясностью не все благополучно. Хотя если перестановки и размещения могут быть с повторениями, то имеет смысл поговорить и о сочетаниях с повторениями.

Замечание. Формула для числа перестановок с повторениями не является частным случаем формулы для числа размещений с повторениями. Их может объединять только то, что в обоих случаях имеют место упорядоченные наборы.

3) Сочетания с повторениями.

Пусть имеются предметы различных типов. Сколькокомбинаций можно сделать из них, если не принимать во внимание порядок элементов? Эту задачу в общем виде можно решать точно так же, как задачу с пирожными.

Пример 3. В кондитерском магазине продаются пирожные 4 сортов: наполеон, эклеры, песочные и слоеные. Сколькими способами можно купить 7 пирожных? Пирожные одного сорта считаются неразличимыми.

Решение. Зашифруем каждую покупку с помощью нулей и единиц. Напишем столько единиц, сколько куплено наполеонов, затем пишем 0, чтобы отделить пирожные одного типа от другого и т.д. Тогда каждой покупке будет соответствовать последовательность из семи единиц и трех нулей в различном порядке. Число всех таких покупок тогда будет равно числу перестановок с повторением:

.

Заметим, что в рассматриваемой последовательности длины 10 из пирожных и разделителей нет никаких ограничений для расстановки разделителей (т.е. нулей). Они могут стоять в начале и в конце последовательности, любые два разделителя могут оказаться рядом. Действительно, здесь мы предполагаем, что покупка может быть абсолютно произвольной (пирожные могут оказаться только одного вида).

Таким образом, задача сводится к выбору трех позиций для разделителей из десяти возможных. Этот выбор можно сделать числом способов, равным . Получили тот же результат.

Определение 2: Группы, составленные из объектов, которые принадлежат одному изтипов элементов, называютсочетаниями с повторениями.

Число всевозможных сочетаний с повторениями обозначают следующим символом: .

Сочетания с повторениями, как было показано в примере, могут быть сведены к перестановкам с повторениями, поэтому имеем формулу:

.

Доказательство. Пронумеруем элементы исходного множества числами от 1 до . Пусть в одно из сочетаний с повторениями вошлоэлементов под номером 1,элементов под номером 2, …,элементов под номером. Поскольку составляются группы изобъектов, то.

Изобразим это сочетание с повторениями в виде последовательности из нулей и единиц. Единица будет обозначать каждый отдельный объект сочетания, нуль – разделитель между группами.

Поскольку сумма всех равна, то в построенной последовательности содержитсяединиц, а так как имеетсяразличных по составу групп, то разделителей (нулей) будет. Верно обратное: каждой такой последовательности соответствует сочетание с определенными повторениями.

Таким образом, задача свелась к поиску ответа на вопрос: сколько различных последовательностей длины можно составить изединиц инулей? Это есть число перестановок с повторениями изединиц инулей:

.

А так как , то формула доказана.

Пример 4. При принятии решения члены комитета голосуют: «за», «против», «воздержался». Сколько может быть возможных исходов голосования по данному решению?

Решение. Если нас интересует, кто и как голосовал, то тогда речь идет о размещениях с повторениями, что даст возможных исходов голосования. Если же не важно, кто и как голосовал, а только общий результат, то тогда речь идет о сочетаниях с повторениями. В этом случае имеем:возможных исходов голосования.

Замечание. Сочетания с повторениями и размещения с повторениями объединяет то, что нет никаких ограничений на число повторений элементов, кроме их общего числа в наборе. Поэтому в формулах идопустим случай, когда. Отличие сочетаний от размещений прежде всего в том, что сочетания – это неупорядоченный набор, а размещения – упорядоченный.