§3. Свойства сочетаний.

Одной из наиболее распространённых комбинаторных формул является формула числа сочетаний. Для упрощения подсчётов и для доказательства некоторых утверждений удобно использовать следующие свойства сочетаний:

, (1)

. (2)

Доказательство. Используем формулу числа сочетаний.

1) .

2) .

Первое из доказанных свойств несет в себе своеобразную симметричность формулы для числа сочетаний. Например, ,. Это свойство упрощает вычисления.

Второе тождество иногда называют тождеством Паскаля. Оно позволяет разбивать на классы и.

Числа возникают в самых разных задачах комбинаторики и теории вероятностей. Например, из тождества Паскаля следует, что для всех натуральных чисели, причем, справедливо равенство:

. (3)

Эта формула может быть доказана индукцией по числу слагаемых в левой части.

Рассмотрим некоторые прикладные аспекты последней формулы.

1) При формула (3) превращается в известную формулу суммы первых членов арифметической прогрессии:

.

Таким образом, можно вычислять сумму слагаемых натурального ряда от 1 до .

2) Для из формулы (3) имеем:

,

или окончательно:

.

Последняя формула дает возможность находить сумму квадратов чисел натурального ряда от 1 до .

3) Для получаем:

,

или после преобразований:

.

Таким образом, можно получить формулы для сумм более высоких степеней натуральных чисел.

Сочетания можно встретить и в школьном курсе математики. Например, в качестве коэффициентов бинома Ньютона выступают именно сочетания.

Бином – это сумма двух слагаемых, например, .

Формула бинома Ньютона в общем виде и её доказательство приводятся в следующей теореме.

Теорема 1: Для любых чисел и, и любого натурального числасправедливо следующее равенство:

. (4)

Доказательство. Применим индукцию по числу .

При :.

Пусть формула верна, для случая, когда степень бинома равна . В этом случае следующее равенство будем считать выполненным:

.

Покажем, что формула выполняется для - й степени:

.

Используя предыдущее равенство и раскрывая скобки, получим требуемое выражение.

В доказательстве можно также использовать свойство: .

Формула (4) носит имя и математика Исаака Ньютона, хотя она была известна задолго до него, например, в Европе ее знал французский математик Блез Паскаль. Заслуга Ньютона состоит в том, что он нашел обобщение этой формулы на случай нецелых показателей. Тем не менее, приведенное выше разложение называют биномом Ньютона, а коэффициенты называютсябиномиальными коэффициентами.

Следствие: Рассмотрим некоторые частные случаи формулы бинома Ньютона:

1) если , то.

2) если , то.

3) Сумма показателей степени при ив любом слагаемом разложения равна.

4) Биномиальные коэффициенты, равноудаленные от концов разложения, равны между собой, так как .

5) Биномиальные коэффициенты сначала возрастают, потом убывают.

Числовые значения биномиальных коэффициентов вычисляются по формуле числа сочетаний: 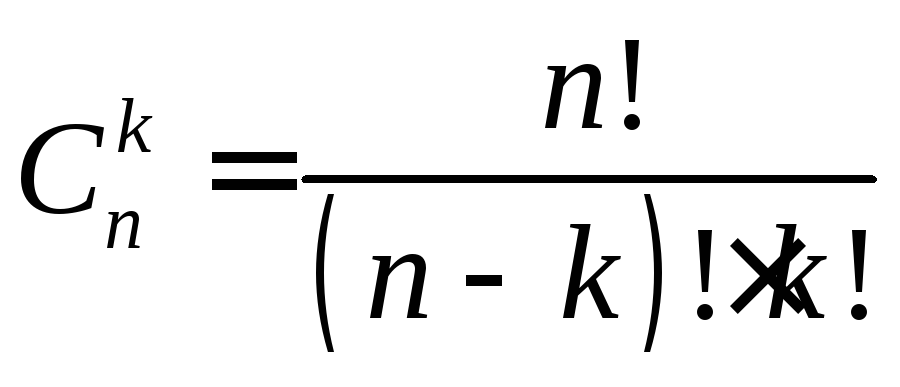. Готовые значения этих коэффициентов располагаются в строкахтреугольника Паскаля.

1 n = 0

1 1 n = 1

1 2 1 n = 2

1 3 3 1 n = 3

1 4 6 4 1 n = 4

1 5 10 10 5 1 n = 5

. . . . . . . . . . . . . . . . . . . . . . . . .

Треугольник Паскаля строится следующим образом. Боковые стороны состоят из единиц. Числа, находящиеся внутри, являются суммой вышестоящих чисел. Каждая строка треугольника соответствует некоторой степени для суммы и содержит соответствующие биномиальные коэффициенты. Таким образом, для того, чтобы раскрыть степень суммы, нужно из треугольника Паскаля взять строку, соответствующую данному показателю степени. Эта строка будет содержать нужные коэффициенты, к которым приписываются соответствующие буквенные выражения. Можно заметить, что строки треугольника Паскаля симметричны, поэтому достаточно взять только половину биномиальных коэффициентов и, если нужно, средний элемент.

Замечание. При , пользуясь треугольником Паскаля, получаем известную школьную формулу квадрата суммы:

.

Аналогично, при имеем формулу куба суммы:

.

Таким образом, можно записать разложение для любого значения показателя .

Если требуется возвести в - ю степень сумму более чем двух слагаемых, то такое выражение называетсяполиномом и является обобщением бинома Ньютона.