Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Восточноукраинский национальный университет им. В. Даля

Предмет:

Дискретная математика

Файл:

Дискретная математика - Лекции 2.doc

Скачиваний:

170

Добавлен:

25.03.2015

Размер:

1.5 Mб

Скачать

☆

1 / 31 2 3 > Следующая >>>

Лекция № 9. Обыкновенные дифференциальные уравнения

Введение

Обыкновенные дифференциальные уравнения (ОДУ) не относятся к области дискретной математики. Мы рассмотрим этот тип уравнений для того, чтобы показать их связь с конечно-разностными уравнениями, которые изучаются в курсе дискретной математики.

Рассмотрим непрерывную функцию , имеющуюn производных: ,, …,.

Уравнение вида

, (9.1)

где и– известные функции, называетсялинейным ОДУ n-го порядка.

Функция заранее неизвестна. Ее получают в ходе решения дифференциального уравнения (9.1). Поэтому эту функцию называютнеизвестной функцией или решением дифференциального уравнения.

В общем случае уравнение (9.1) имеет бесконечное множество решений. Чтобы выделить из них единственное решение, нужно задать начальные условия: ,, …,.

Если какая-либо из производных в уравнении: ,, …,, либо сама функция, возведена в степень, отличную от первой, то такое дифференциальное уравнение называетсянелинейным.

В частном случае, вместо функций , в уравнение (9.1) могут входить постоянные коэффициенты(не зависящие от). Тогда дифференциальное уравнение называетсяуравнением с постоянными коэффициентами.

Обыкновенные дифференциальные уравнения часто возникают при решении разнообразных физических, технических, экономических и социальных задач.

Пример 9.1. Рассмотрим электронную схему, показанную на рис. 9.1.

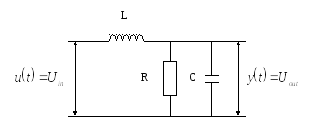
Рис. 9.1. -цепь

Схема состоит из катушки индуктивностью , резистора сопротивлением и конденсатора емкостью. Падение напряжения на катушке определяется выражением

, (9.2)

, (9.3)

где – это время, – ток, протекающий через резистор,– ток, протекающий через конденсатор. На основании (9.2) и (9.3) можем записать

После преобразований получим линейное дифференциальное уравнение второго порядка:

В общепринятых обозначениях

. (9.4)

Для данной электронной схемы известная функция имеет смысл входного сигнала, а неизвестная функция– это зависимый отвыходной сигнал. Задавая входной сигнал и решая ОДУ (9.4), можно получать соответствующие значения выходного сигнала. Поэтому дифференциальное уравнение (9.4) является математической моделью электронной схемы, с помощью которой можно исследовать работу схемы теоретически, не собирая ее из электронных компонентов.

Операционное исчисление

Существуют различные способы решения дифференциальных уравнений. В данном разделе мы ознакомимся со способом, использующим операционное исчисление. Этот способ применяется к линейным ОДУ, он позволяет преобразовывать дифференциальное уравнение в алгебраическое.

Изобретателем операционного исчисления является Оливер Хевисайд (1859-1925), английский ученый и инженер. Он ввел оператор дифференцирования, который обозначил латинской буквой (сейчас этот оператор принято обозначать буквой) и разработал правила обращения с этим оператором.

Пример 9.2. Применим метод Хевисайда к уравнению (9.4):

Предположим, что на вход схемы подан ступенчатый входной сигнал

а на выходе в начальный момент времени имеем: ,(нулевые начальные условия). Исходное уравнение при преобразуется к следующему виду:

Затем Хевисайд преобразовывал дифференциальное уравнение в алгебраическое, при этом оператор дифференцирования превращался в обычную переменную . Неизвестная функцияпри переходе обращалась в произведение:, производная первого порядка в:, производная второго порядка – в:.

Решая это алгебраическое уравнение относительно , приходим к уравнению

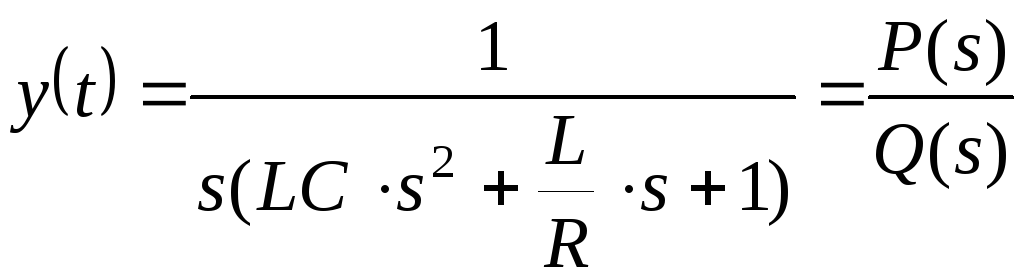Полученное уравнение еще не является окончательным. Необходимы преобразования, позволяющие перейти от переменной к переменной, являющейся аргументом функции. Эти преобразования производятся в соответствии с алгоритмом:

где – корни уравнения,.

После преобразований окончательно получим

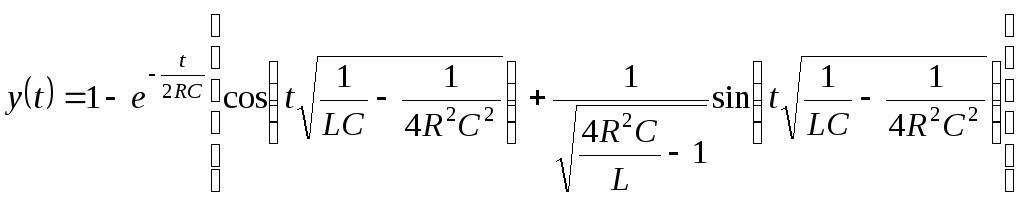График функции при значениях параметровR=1; C=2; L=0,1 – показан на рис. 9.2.

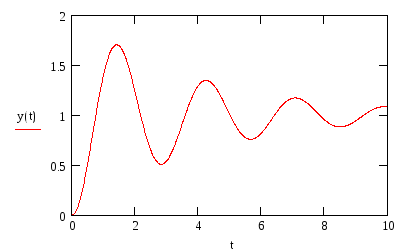
Рис. 9.2. Реакция -цепи на ступенчатый входной сигнал

Преобразование Лапласа

Хевисайд не дал строгого математического обоснования своего метода. Это было сделано позже с помощью интегрального преобразования Лапласа. В результате такого преобразования функция , зависящая от переменнойи называемаяоригиналом, преобразуется в функцию , называемуюизображением (она зависит от комплексной переменной ):

. (9.5)

Обратное преобразование Лапласа определяется формулой:

, . (9.6)

Чтобы интегралы (9.5) и (9.6) сходились, оригинал должен удовлетворять следующим условиям.

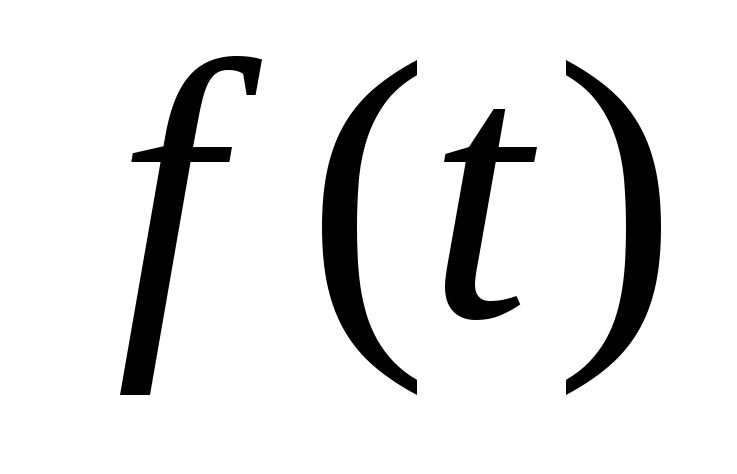–однозначная, непрерывная или кусочно-непрерывная вместе со своими производными -го порядка при;
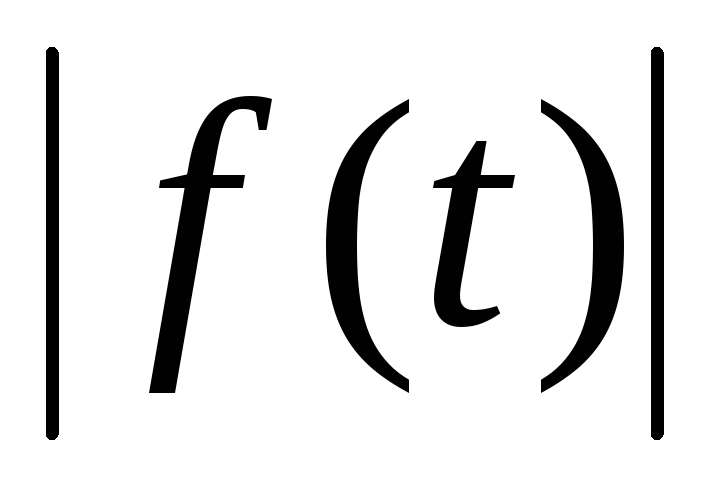растет не быстрее, чем некоторая показательная функция, что означает существование таких постоянных положительных чисел 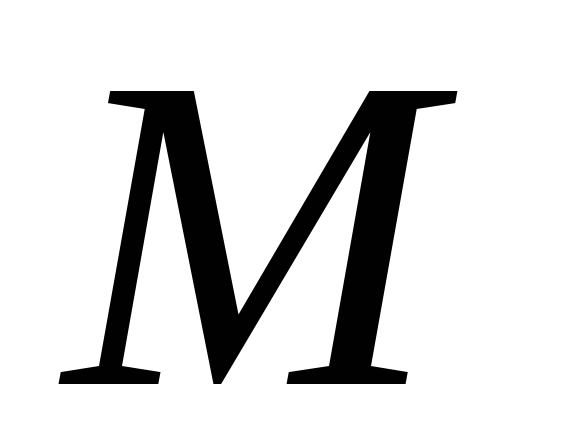и, не зависящих от, при которых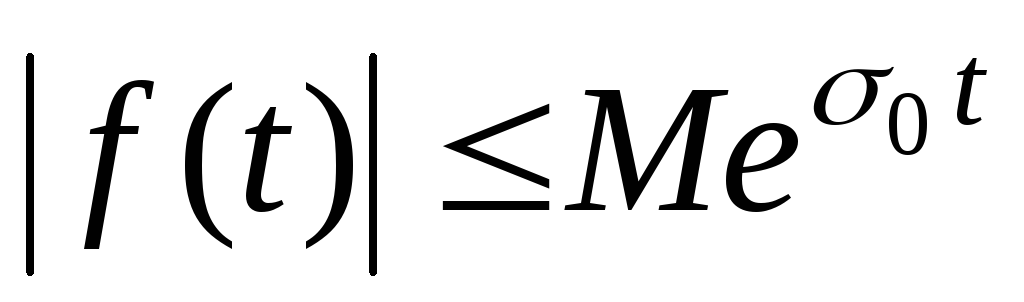для всех;
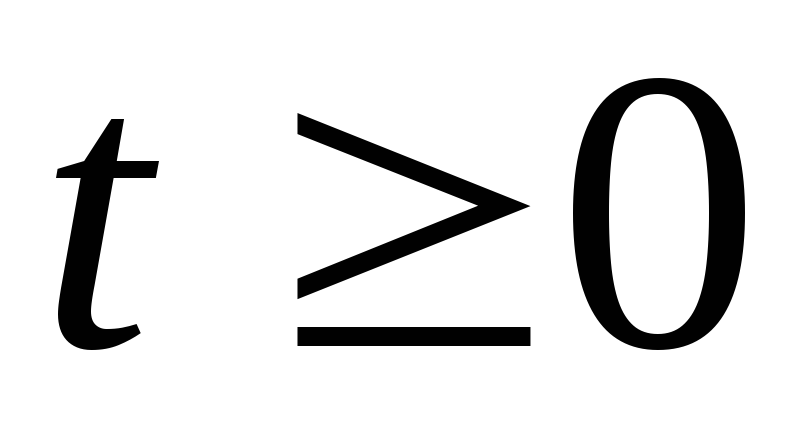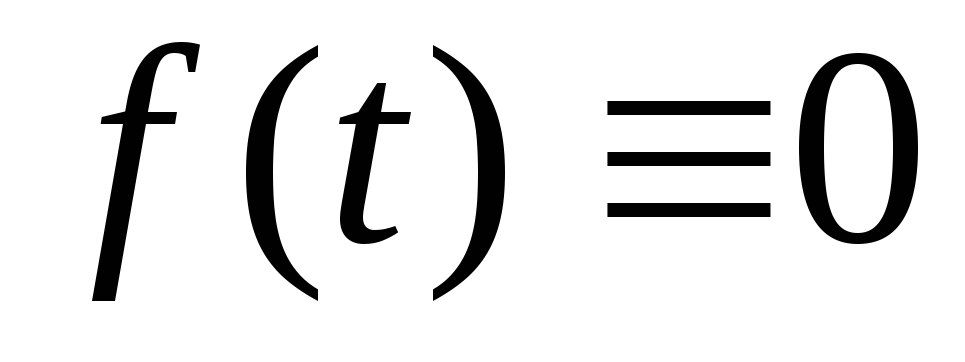при .

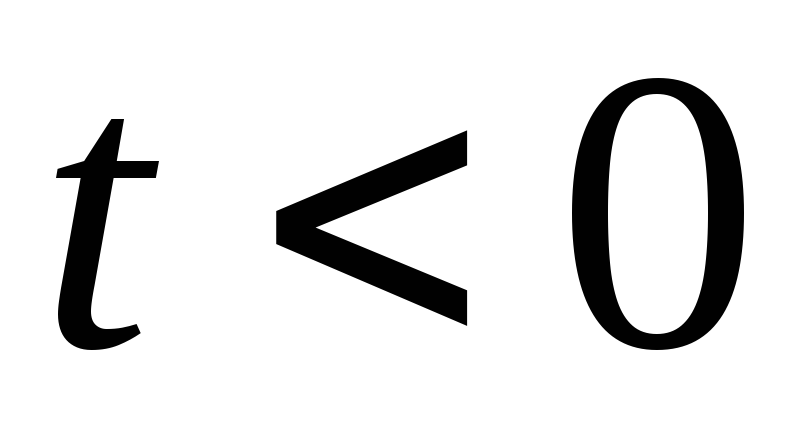Соответствие между изображением и оригиналом обозначают следующим образом:

или ,

, .

Помимо изображения по Лапласу применяется также изображение функции по Карсону (или по Хевисайду)

отличающееся от преобразования Лапласа множителем . В последнее время в технической литературе все чаще пользуются изображением по Лапласу. Это объясняется наличием наглядной связи между операторным методом и гармоническим анализом, вносящей физический смысл в понятие изображения (изображение по Лапласу– это спектральная функция по отношению к затухающей функции, для которой переменнаяявляется частотой).

Свойства изображений

Если два изображения 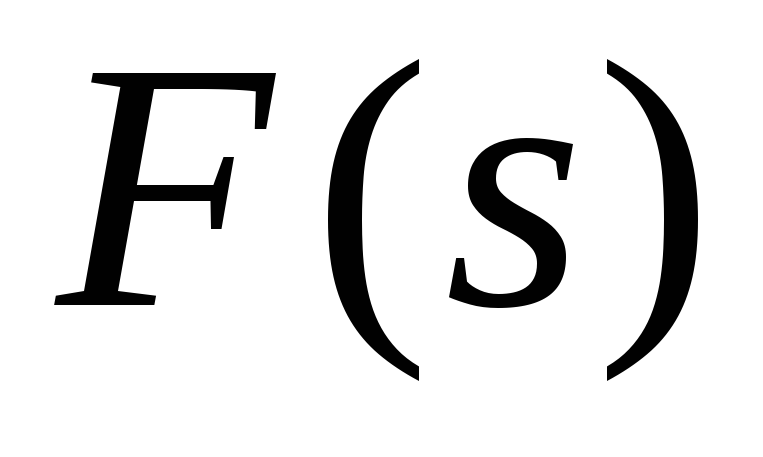и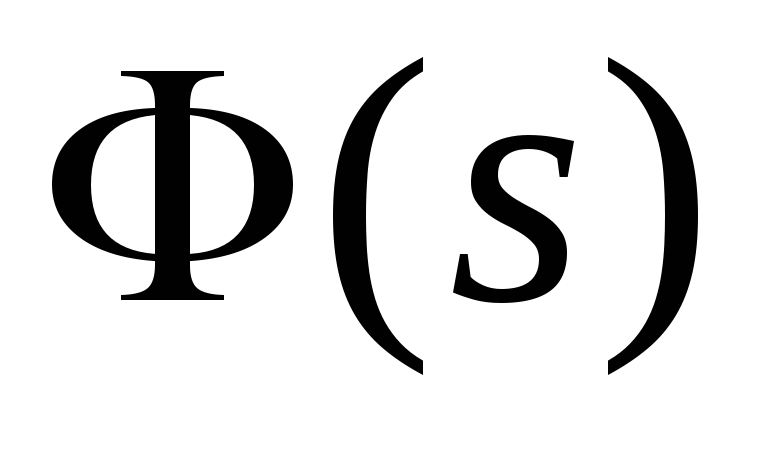совпадают, то совпадают между собой и соответствующие оригиналы во всех точках, за исключением, быть может, точек разрыва.
Всякое изображение 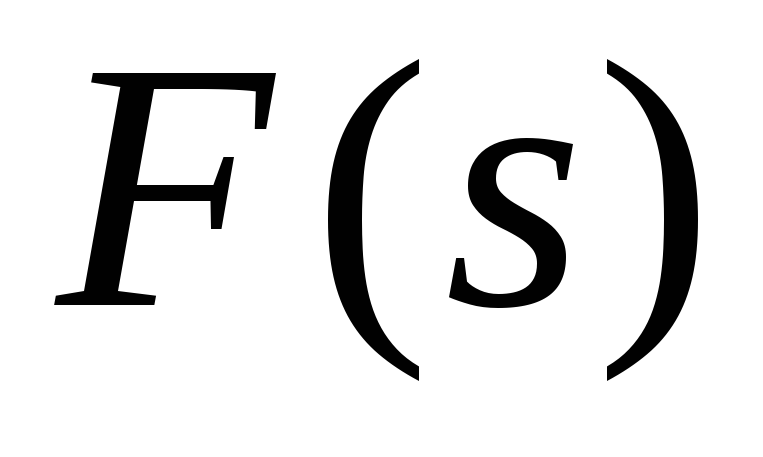при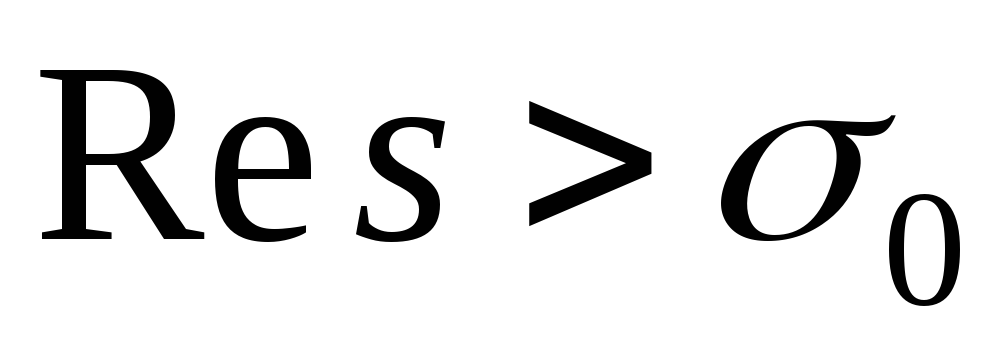является аналитической функцией, то есть может быть разложено в степенной ряд и следовательно, неограниченное число раз интегрируемо и дифференцируемо в области сходимости ряда.
Свойство линейности: если 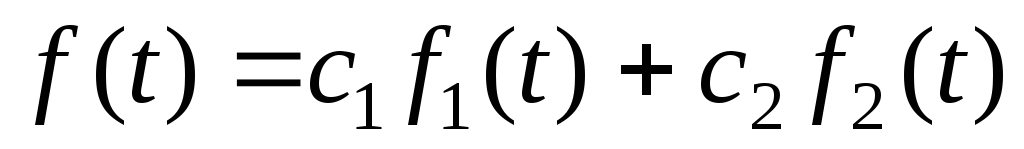и при этом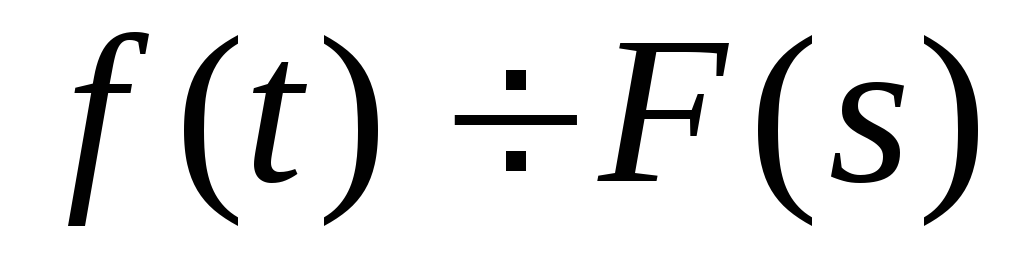,,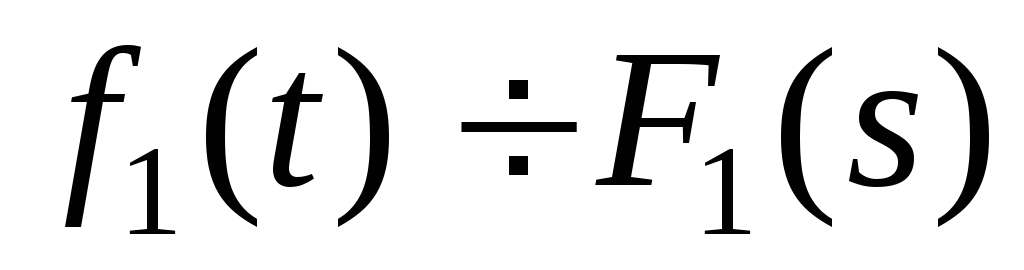, 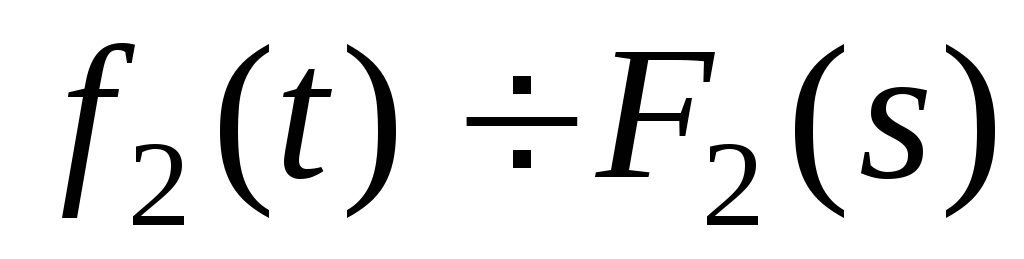то.

Изображения некоторых функций

1. Функция Хевисайда :

Непосредственным интегрированием находим

. (9.7)

2. Изображения показательных функций:

, (9.8)

. (9.9)

Если , где, тои.

Изображения гиперболических функций:

, (9.10)

. (9.11)

Изображения тригонометрических функций:

, (9.12)

. (9.13)

Изображение функции: .

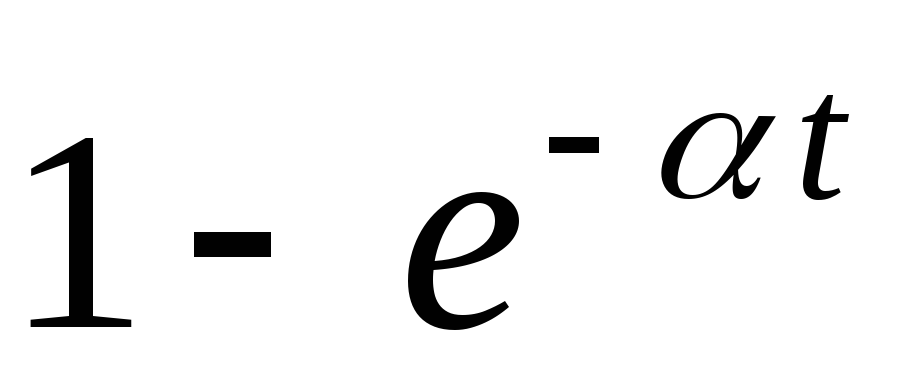. (9.14)

Изображения производных от функции 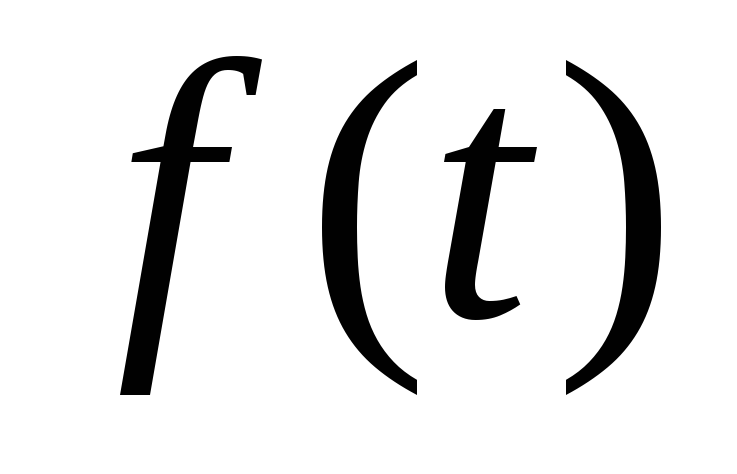легко получить с помощью интегрирования по частям:

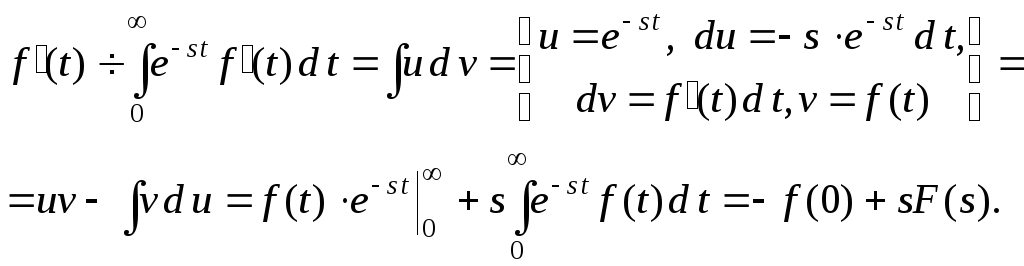
Отсюда следует:

. (9.15)

Аналогично можно получить:

, (9.16)

, (9.17)

. (9.18)

7. Изображение интеграла от функции:

Пусть и, причем

Так как , то.

Поскольку , то. Окончательно имеем:

. (9.19)

Основные теоремы операционного исчисления

В большинстве случаев применение операционного исчисления к решению задач укладывается в следующую схему. Пусть требуется найти некоторый результат в виде функции , для получения которого без использования операторного метода надо над заданной функциейвыполнить какую-то операциюA.

Применяя операционное исчисление, сначала переходят от оригинала к его изображению, а затем над этим изображением выполняют операциюB, соответствующую в области оригиналов операции A (например, делят изображение на вместо интегрирования функции), и получают промежуточный результат – изображение. Затем переходят от изображения к искомому оригиналу.

На первый взгляд, схема решения задачи удлиняется. Однако на самом деле получается значительный выигрыш как в средствах вычисления, так и во времени. В частности, везде дифференцирование заменяется умножением на , а интегрирование – делением на.

Этот выигрыш достигается путем применения основных теорем операционного исчисления и известных «табличных» изображений, публикуемых в справочниках.

Рассмотрим основные теоремы операционного исчисления.

Теорема 9.1. (о дифференцировании изображения).

Если , то.

Доказательство: .

Следствие 9.1.1: .

Следствие 9.1.2: . (9.20)

Пример 9.3. Найти изображение функции . Поскольку, то.

Теорема 9.2. (об интегрировании изображения).

Если , то.

Доказательство. Обозначим и. Очевидно, что, и по предыдущей теореме:

Отсюда следует: .

Постоянная интегрирования определяется из условия: .

. Таким образом

Теорема 9.3. (об изменении масштаба).

Для всегда.

Доказательство. Обозначим . Тогда

Пример 9.4. Известно, что . Найти изображение функции.

Теорема 9.4. (запаздывания).

Если и, то.

Доказательство. Обозначим . Тогда

Теорема 9.5. (упреждения).

Если и, то.

Доказательство. Обозначим . Тогда

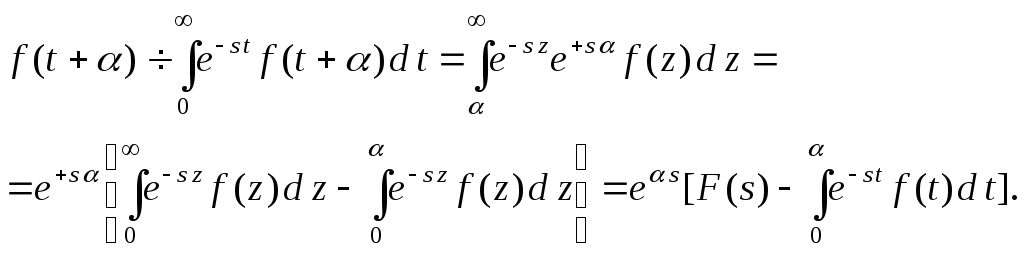
Теорема 9.6. (смещения).

Если и, то.

Доказательство.

Теорема 9.7. (о свертке).

Если и, то

Замечание. Интеграл называется сверткой функцийи, и обозначается:. Можно показать, что свертка двух оригиналов также является оригиналом.

Доказательство теоремы о свертке.

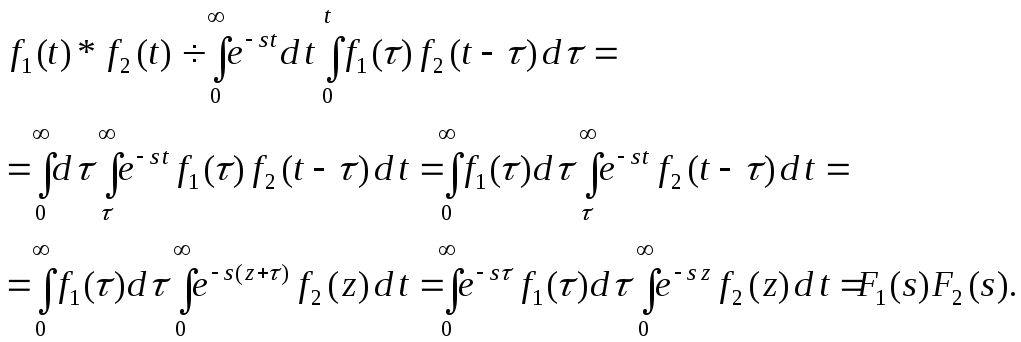
Пример 9.5. Применяя теорему о свертке, найти оригинал изображения:

Решение. Имеем ,

, .

Поэтому .

Теорема 9.8. (первая теорема разложения).

. (9.21)

Доказательство. Формула (9.21) прямо следует из формулы (9.20).

Пример 9.6. Найти оригинал изображения .

Решение. Известно, что логарифмическая функция может быть разложена в следующий степенной ряд:

В соответствии с первой теоремой разложения получаем:

Теорема 9.9. (вторая теорема разложения).

Если – рациональная правильная несократимая дробь, а– простые (не кратные) корни уравнения:, то

, (9.21)

где ,.

Доказательство. Прежде всего, заметим, что требование правильности дроби в данной теореме обязательно, так как эта дробь – изображение, и должно быть выполнено условие .