Министерство образования и науки украины восточноукраинский национальный университет им. В. Даля

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

по дисциплине

«КОМПЬЮТЕРНАЯ ТЕХНИКА И ПРОГРАМИРОВАНИЕ»

тема: «МАТЕМАТИЧЕСКИЙ ПАКЕТ MATHCAD 11. ЛАБОРАТОРНЫЙ ПРАКТИКУМ»

(для студентов технических специальностей)

У Т В Е Р Ж Д Е Н О

на заседании кафедры

«Компьютерные системы и сети»

Протокол № от

Луганск, ВНУ им. В. Даля, 2007

УДК

Методические указания по дисциплине «Компьютерная техника и програмирование», тема «Математический пакет MathCad 11. Лабораторный практикум» / Сост.: Ю.В. Полупан – Луганск: Изд-во Восточноукр. Нац. ун-та, 2006. – стр.

В методических указаниях изложен перечень лабораторных работ по теме «Математический пакет MathCad 11», приведены образцы выполнения данных работ с подробным объяснением хода решения.

Рассматриваются типы данных, применяемых в документах MathCad, и принципы их ввода-вывода в наиболее простой числовой форме. Приведена методика работы с массивами, которые реализованы в виде векторов и матриц, что максимально приближает стиль вычислений к общепринятой математической форме.

Рассматриваются возможности символьного процессора MathCad 11, что позволяет решить многие задачи математики аналитически, без применения численных методов и, соответственно, без погрешностей вычислений.

Так же в методических указаниях разработаны лабораторные работы, в которых рассматривается решение алгебраических нелинейных уравнений и систем таких уравнений.

Составители: О.С. Петров, проф.,

Ю.В. Полупан, асс.

Отв. за выпуск: Петров А.С.

Рецензент:

Методические указания представляют MathCad 11, перечень лабораторных работ, предназначенных для выполнения в математическом пакете MathCad 11, с подробным описанием решения данных задач. При этом в качестве примеров применения системы MathCad 11 взяты расчеты, наиболее часто встречающиеся при решении типовых задач в курсе «Высшая математика» университетов и вузов.

Лабораторная работа №1 Решение систем линейных уравнений методом Крамера, обратной матрицы и методом Жордана-Гаусса. Векторная алгебра.

Задача I.

Решить заданную систему уравнений, пользуясь формулами Крамера, методом обратной матрицы и методом Жордана-Гаусса.

x - 2y + 3z = 6;

2x + 3y - 4z = 16;

3x - 2y - 5z = 12

Выполнение:

Метод Крамера

1. Изначально необходимо ввести матрицу системы и матрицу свободных членов. Для данного случая:

– матрица системы;

– матрица свободных членов.

а) Для ввода матрицы А щелкните в том месте рабочего окна, в котором хотите создать матрицу A. Введите обозначение А и оператор := . Вызовите на экран панель инструментов (Матрицы) с помощью последовательности команд: меню Вид - Панели инструментов - Матрицы. Окно имеет вид, изображенный на рис. 1.

Рис. 1.

Активизируйте кнопку под названием (Создать матрицу или вектор). В появившемся диалоговом окне (рис. 2) введите количество строк (Rows) и количество столбцов (Columns) для создаваемой матрицы А. В вашем случае количество строк 3, количество столбцов 3.

Рис. 2.

После выполненных действий в рабочем окне документа появится матрица, в которую необходимо ввести коэффициенты при неизвестных. При введении коэффициентов можно использовать клавишу Tab.

б) Для ввода вектора В щелкните в том месте рабочего окна, в котором хотите создать вектор В. Введите обозначение В и оператор := . Вызовите на экран панель инструментов (Матрицы) (в том случае, если она па экране отсутствует) с помощью последовательности команд: меню Вид - Панели инструментов - Матрицы. Окно имеет вид, изображенный на рис. 1.

Активизируйте кнопку под названием (Создать матрицу или вектор). В появившемся диалоговом окне (рис. 2) введите количество строк (Rows) и количество столбцов (Columns) для создаваемого вектора В. В нашем случае количество строк 3, количество столбцов 1.

После выполненных действий в поле рабочего документа появится вектор-столбец, в который необходимо ввести коэффициенты при свободных членах решаемой системы. При введении коэффициентов можно использовать клавишу Tab.

2) Вычислим определитель матрицы А. Для этого следует щелкнуть в том месте рабочего листа, где планируется поместить определитель. Щелкните на кнопке (Вычисление определителя) наборной панели (Матрицы). В пустой местозаполнитель появившейся записи внесите имя матрицы|А| и активизируйте клавишу =.

Полученная запись будет иметь вид: |А| = и появится значение определителя матрицы А. Если определитель равен 0, то данная система имеет больше одного решения и не имеет смысла дальнейшее её решение. Если определитель не равен 0, то система имеет единственное решение, которое может быть определено с помощью метода Крамера.

3. Введите матрицы А1, А2, A3 аналогично матрице А. Матрица А1 получается из матрицы А заменой первого столбца в матрице А на столбец свободных членов В, то есть для данной системы имеем:

.

Матрица А2 получается из матрицы А заменой второго столбца в матрице А на столбец свободных членов В, то есть для данной системы имеем:

Матрица A3 получается из матрицы А путем замены третьего столбца на столбец свободных членов В. Матрицу А3 сформировать самостоятельно.

4) Вычислите определители матриц Al, A2, A3. Для этого установите курсор в ту область рабочего листа, где хотите вычислить определитель и активизируйте кнопку (Вычисление определителя) (рис. 1). Создайте запись =. Аналогично вычислите определители матриц А2 и A3 создав записи = и = .

5) Далее, согласно методу Крамера, создайте формулы для вычисления переменных х, у, z и вычислите их.

Формула для вычисления перемененной х: . Для определения непосредственно значения переменной х, установитекурсор правее или ниже данной формулы и напишите х=.

Формула для вычисления у: . Для определения непосредственно значения переменной у, установите курсор правее или ниже данной формулы и напишите у=.

Формула для вычисления z: . Для определения непосредственно значения переменной z установите курсор правее или ниже данной формулы и напишите z=.

Матричный метод

1) При решении системы линейных уравнений данным методом ответом будет являться вектор-столбец, который будет состоять из значений переменных х, у, z, при которых данная система преобразуется в тождество.

2) Для решения системы матричным методом запишите формулу решения системы матричным методом. Формула для данного случая имеет вид: , где R - вектор-столбец, состоящий из значений решения системы. Для получения значений искомых переменных установите курсор правее или ниже данной формулы и напишите R=.

Получим:

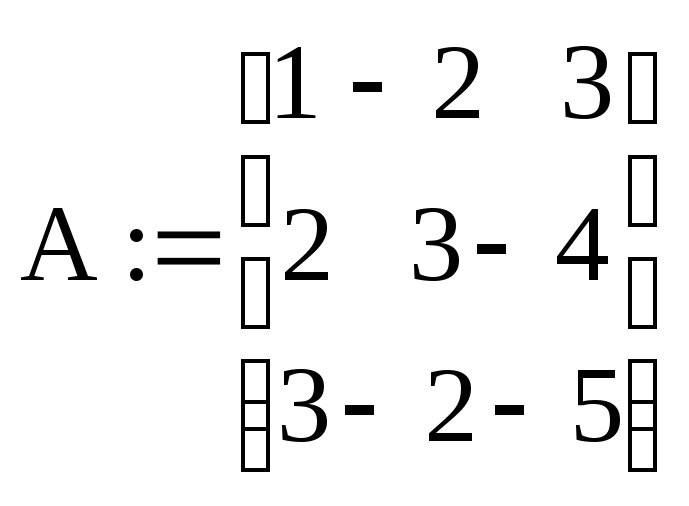
3. Решение будет иметь вид . Это значит, чтоx=7, y=2, z=1. Значения переменных x, y, z, полученные матричным методом, должны быть в точности равны значениям этих перемнных, полученных методом Крамера. Если значения не совпадают, знпачит, в ходе решения либо по методу Крамера либо по методу обратной матрицы были допущены ошибки.

Метод Жордана -Гаусса

1) При решении системы линейных уравнений данным методом ответом будет являться вектор-столбец, который будет состоять из значений переменных x, y, z при которых данная система переобразуется в тождество.

2) Для решения системы методом Жордана-Гаусса запишите формулу, включающую функцию lsolve. Если переменная А обозначает систему, а переменная В обозначает матрицу свободных членов, то данная формула запишется следующим образом: . Для получения значений искомых переменных установите курсор правее или ниже данной формулы и напишите. Получим:

3. Значения переменных x, y, z, полученные методом Жордана-Гаусса, должны быть в точности равны значениям этих перемнных, полученных методом Крамера и методом обратной матрицы. Если значения не совпадают, значит, в ходе решения либо по методу Крамера либо по методу обратной матрицы были допущены ошибки.

Задача II.

Даны координаты вершин А1=(2, -3, 5), А2=(0,2,1), А3=(-2,-2,3), А4=(3,2,4). Средствами векторной алгебры найти:

а) длину ребра А1А2;

б) угол между ребрами А1А2 и А1А3;

в) площадь грани А1А2А3;

г) объём пирамиды А1А2А3А4;

д) высоту пирамиды.