Лабораторная работа №6 Решить систему линейных алгебраических уравнений методом вращений.

Изученные теоретические вопросы:

Вещественные унитарные матрицы

называются элементарными матрицами вращения или матрицами простого поворота. При умножении матрицы 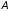слева на матрицу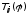получим матрицу, у которой изменятся в отличие от матрицытолько-я и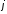-я строки. Изменение элементов-й и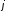-й строк осуществляется по формулам

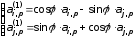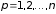, . (4.17)

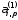Всегда можно подобрать угол поворота так, чтобы элементоказался равным нулю. Для этого нужно взять

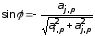, , (4.18)

есл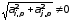и , и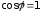,в противном случае.

Теорема 4.3. Любая действительная матрица преобразуется в верхнюю треугольную матрицу после умножения слева на конечную цепочку матриц простого поворота .

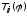Рассмотрим систему (4.1) и построим для матрицы 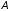системы унитарную матрицу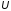так, чтобы матрица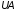преобразованной системы стала верхней треугольной. Тогда система преобразуется к виду

.

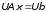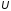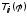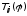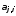Матрица представляет собой произведение унитарных матриц простого поворота. Матрицастроится так, чтобы после умножения обнулить элемент, стоящий под главной диагональю. В этом случае угол поворота выбирается по формулам (4.18).

Решение:

void main(){

int i,j,j1,jj,n,p,l;

float A[4][4],D[4][4],D1[4][4],S[4],L[4],X[4],W[4],U[4][4],U1[4][4],m,r,t,y,k;

clrscr();

printf("Vvedite razmernost matrix\n");

scanf("%d",&n);

printf("Vvedite elementi matrici\n");

for(i=0;i<n;i++)

for(j=0;j<=n;j++)

scanf("%f",&A[i][j]);

for(i=0;i<n;i++)

for(j=0;j<=n;j++)

{

D[i][j]=A[i][j];

U[i][j]=0;

}

for(i=0;i<n;i++)

U[i][i]=1;

for (i=0;i<n;i++)

for(j=0;j<=n;j++)

U1[i][j]=U[i][j];

for(i=0,p=0;i<n-1;i++,p++)

{

for(j=1;j<n;j++)

{

k=D[i][p]/sqrt(D[i][p]*D[i][p]+D[j][p]*D[j][p]);

m=-D[j][p]/sqrt(D[i][p]*D[i][p]+D[j][p]*D[j][p]);

U1[i][i]=k;

U1[i][j]=-m;

U1[j][i]=m;

U1[j][j]=k;

for(l=0;l<n;l++)

{

for(j1=0;j1<=n;j1++)

{

t=0;

for(jj=0;jj<n;jj++)

t+=U1[l][jj]*D[jj][j1];

D1[l][j1]=t;

}

}

for(l=0;l<n;l++)

for(j1=0;j1<=n;j1++)

{

D[l][j1]=D1[l][j1];

U1[l][j1]=U[l][j1];

}

}

}

X[n-1]=D[n-1][n]/D[n-1][n-1];

for(i=n-2;i>=0;i--)

{

t=D[i][n];

for(j=n-1;j>i;j--)

t-=D[i][j]*X[j];

X[i]=t/D[i][i];

}

printf("korni uravneniya\n");

for(i=0;i<n;i++)

printf("%.2f\n",X[i]);

getch();

}

Результат:

Введенные данные	Полученный результат	Проверка
	-8.30 0.17 -2.76	-2,7 1,5 -1.20

Лабораторная работа№7 Тема: «Прямые методы решения систем линейных алгебраических уравнений»

Постановка задачи:

Решить систему линейных алгебраических уравнений методом ортогонализации