5.3 Двоичный сумматор.

Рассмотрим построение логической схемы на примере одноразрядного сумматора, выполняющего арифметическое сложение двоичных чисел и,-го разряда и переноса из младшего разряда. Пусть– получаемая сумма, а– перенос в старший разряд, тогда получаем следующую таблицу истинности такого сумматора.

0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

Отсюда получаем ;

.

Построим схему, соответствующую данному сумматору. Для этого вначале упростим выражение для . Как легко заметить, выражение дляне упрощается, при использовании предыдущих методов. Для упрощения выражения функциииспользуем выражение функции.

Поэтому будем рассматривать как переменную величину. В результате получаем следующую таблицу, которая содержит избыточные наборы переменных:

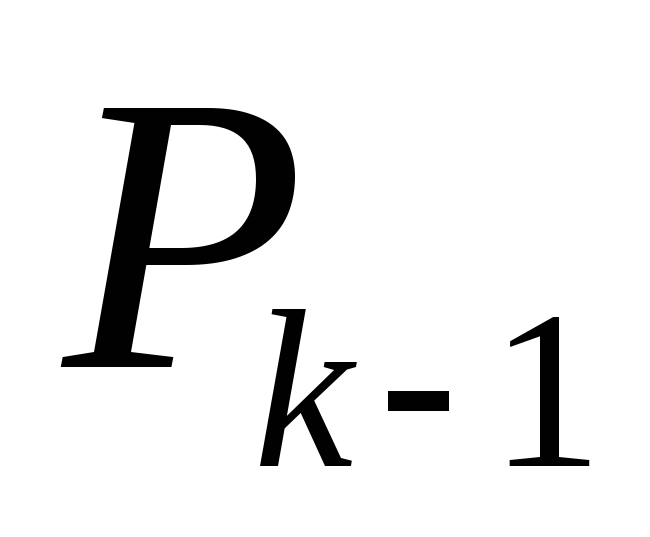
0	0	0	0	0
0	0	0	1
0	0	1	0	1
0	0	1	1
0	1	0	0	1
0	1	0	1
0	1	1	0
0	1	1	1	0
1	0	0	0	1
1	0	0	1
1	0	1	0
1	0	1	1	0
1	1	0	0
1	1	0	1	0
1	1	1	0
1	1	1	1	1

Отсюда .

Используя методы, которые будут рассмотрены в теме 6, нетрудно упростить выражение для :

=,

где .

Теперь строим логическую схему:

Вопросы для самоконтроля

1 Что такое релейно-контактная схема?

2 Почему любую булеву функцию можно изобразить в виде релейно-контактной схемы?

3 В чем состоит проблема анализа релейно-контактных схем?

4 В чем состоит проблема синтеза релейно-контактных схем?

5 Что такое логические элементы?

6 Приведите геометрическое изображение логических элементов.

7 Что такое логическая схема и двоичный сумматор?

Тема 6 минимизация булевых функций

6.1 Сокращенная и тупиковая ДНФ

6.2 Метод импликантных матриц

Цель данного раздела – изложение основных методов построения минимальных дизъюнктивно нормальных форм.