Пример выполнения работы

Задача. В таблице 1 приведены денежные затраты Х на животноводство, заданные выборкой по 60 хозяйствам области, дес. тыс. руб. на 100 голов.

Таблица 1

X	X	X	X	X	X
41 49 23 25 38 67 56 47 49 31	40 41 38 49 63 48 37 60 42 51	30 42 53 27 44 39 62 54 41 38	52 43 40 50 68 50 38 49 41 44	57 39 43 20 51 42 35 61 33 67	39 18 40 39 60 51 59 53 59 31

Требуется для признака х:

1. Построить интервальный ряд распределения; для каждого интервала подсчитать локальные, а также накопленные частоты; построить вариационный ряд;

2. Построить полигон и гистограмму;

3. Определить выборочную среднюю; а также низшую и высшую частные средние; моду и медиану; дисперсию и среднее квадратическое отклонение; коэффициент вариации;

4. Проверить при уровне значимости 0,05 гипотезу о нормальном законе распределения соответствующего признака с помощью критериев согласия χ² ─ Пирсона и 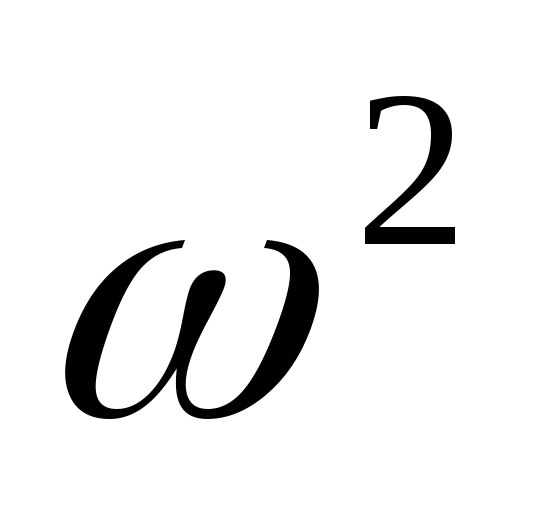─ Смирнова;

5. Найти точечные и интервальные оценки генеральной средней и среднего квадратического отклонения (при доверительной вероятности р = =0,95);

6. Найти ошибки выборочных оценок;

7. Произвести анализ всех вычисленных статистических параметров.

Решение.

1) Составим интервальный ряд для признака Х. Для этого найдём размах варьирования значений признака по формуле: R_Х =X_max - X_min.

Из таблицы 1 следует: X_max = 68 ; X_min = 18 и R_Х = 68 - 18 = 50.

Число интервалов m, на которые следует разбить интервал значений признака, найдём по формуле Стерджеса: m = 1+3,322 lg n, где n - объём выборки, то есть число единиц наблюдения.

В нашем примере n=60. Получим: m = 1+3,322•lg 60 = 1+3,322•1,778 = =6,9 ≈7. Таким образом, следует образовать 7 интервалов.

Теперь рассчитаем шаг (длину частичного интервала) h по формуле: h= =7,1. Округление шага производится, как правило, в большую сторону. Таким образом, принимаем h=8.

За начало первого интервала принимаем такое значение из интервала (Х_min; X_min- ), чтобы середина полученного интервала оказалась удобным для расчетов числом. В нашем случае за нижнюю границу интервала возьмём X_min - 2 = 18 - 2 = 16. В результате получим следующие границы интервалов: 16-24-32-40-48-56-64-72.

Теперь произведём разноску значений признака по интервалам и подсчитаем число вариант, попавших в каждый из них, применяя так называемый метод конверта, когда каждую варианту, попавшую в интервал, обозначают точкой или отрезком. Варианты, совпадающие с границами частичных интервалов, включают в правый интервал. В табл. 2 произведена разноска значений признака Х, указаны интервалы, середины интервалов, частоты n_i, которые представляют собой число вариант, попавших в данный интервал, и накопленные частоты, равные сумме частот значений признака Х, попавших в предшествующие интервалы. Интервалы и их частоты представляют собой интервальный ряд. Середины интервалов и соответствующие частоты дают вариационный ряд (табл. 3).

Таблица 2