Лабораторная работа № 19

ИЗМЕРЕНИЕ АКТИВНОГО, ЕМКОСТНОГО И ИНДУКТИВНОГО СОПРОТИВЛЕНИЙ В ЦЕПИ ПЕРЕМЕННОГО ТОКА

ЦЕЛЬ РАБОТЫ: изучение цепей переменного тока с активным, емкостным и индуктивным сопротивлениями.

ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ: переносной измерительный комплект К-50, ламповый реостат, катушка индуктивности, конденсаторы, соединительные провода.

1. КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Рассмотрим цепь, содержащую только резистор R с омическим сопротивлением R (рис. 1).

Сопротивление R резистора называют активным, так как в нем происходит необратимая потеря электрической энергии, переходящей в тепловую.

Рис.1

К зажимам цепи приложено переменное напряжение

U_R = U_max * Cos t (1)

где u_max – амплитудное значение напряжения, - круговая частота.

Величину тока, проходящего через резистор, определим исходя из закона Ома:

t = J _max cos t (2)

где - амплитудное значение силы тока. Из формул (1) и (2) видно, что сила тока и напряжение на активном сопротивлении изменяются в одной фазе – гармонически (рис.2), их можно представить с помощью векторной диаграммы (рис.3).

Вектор, изображающий амплитудное значение силы тока J_max , обычно откладывается вдоль горизонтальной оси, взятой за начало отсчета.

Рис.2

Угол между амплитудным значением тока и напряжением называют фазовым. В цепи, содержащей только активное сопротивление, сдвиг фаз между силой тока и напряжением отсутствует, а поэтому вектор напряжения будет направлен так же, как и вектор тока, т.е. вдоль оси токов (рис.3).

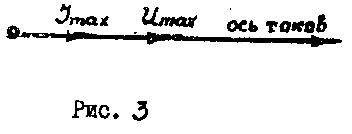
Рассмотрим цепь, содержащую катушку индуктивности с индуктивностью L (рис.4), омическое сопротивление которой будем считать равным нулю.

Рис.4

Напряжение на зажимах цепи будет:

U_L = U_max * cos t (3)

По закону Ома для участка цепи при R = 0 будем иметь

U_L = ₁ - ₂ = _L (4)

(будем считать, что приложенное напряжение уравновешивается электродвижущей силой самоиндукции, равно ей по значению и противоположно по направлению),

где _L - ЭДС самоиндукции, которая по основному закону электромагнитной индукции будет равна:

_L = - L (5)

Учитывая формулы (3) , (4) и (5), получим :

U_max Cos t = L(6)

Выделив переменные в (6) и проинтегрируя его, найдем :

I = Sint = J_max cos (t -) , (7)

где I_max = - амплитудное значение тока. R_L = L – называется индуктивным сопротивлением. На индуктивном сопротивлении не происходит потери энергии и его называют реактивным сопротивлением.

Из (7) и (3) следует, что сила тока отстает от напряжения (рис. 5). Причиной этого является ЭДС самоиндукции. На рис. 6 представлена векторная диаграмма напряжения и тока в цепи с индуктивностью.

Рассмотрим цепь, содержащую конденсатор емкостью С (рис. 7).

Напряжение на зажимах цепи:

U_c = U_max cos t (8)

А сила тока

I = , (9)

На основании (8) получим:

I = - U_max c Sint = J_max Cos (t +), (10)

где J_max = U_max c (11)

J_max - амплитудное значение силы тока.

Величина

называется емкостным сопротивлением и так же как индуктивное называется реактивным сопротивлением. Оно зависит от емкости конденсатора и частоты.

Из /8/ и /10/ следует, что в цепи с емкостным сопротивлением напряжение на конденсаторе отстает по фазе от колебаний силы тока на величину π/2.

Векторная диаграмма полученных результатов представлена на рис.9.

Рассмотрим цепь, содержащую резистор, катушку и конденсатор /рис.10/.

Как было изложено выше, сила тока в цепи и напряжение изменяются не в одной фазе, т. е. если сила тока изменяется по закону:

то напряжение по закону :

где φ-сдвиг фаз между током и напряжением. Полное сопротивление цепи называется импедансом и обозначается Ż.

Для нахождения импеданса и сдвига фаз, воспользуемся векторной диаграммой / рис.11/.Амплитуды напряжений на всех участках будем откладывать относительно силы тока, т.к. она во всей цепи одинакова. На резисторе векторы напряжения и силы тока совпадают, т.к. они не имеют разности фаз.

На индуктивном сопротивлении вектор напряжения опережает силу тока по фазе на π/2, а на емкостном- отстает на π/2. Результирующий вектор найдем путем сложения трех векторов. Векторы U_maxL иU_maxCнаправлены по одной прямой в противоположные стороны. Полученные векторы (U_maxL-U_maxC) иU_maxRскладываются по правилу параллелограмма и находится результирующий векторU_max0,т.е.:

/13/

Учитывая, что

; U_maxL=I_max*ωL; U_maxc=I_max*. (14)

получим:

I²_max R²₀=J²_max R²+J²_max (R_L–R_c)²(15)

Обозначим R₀черезZ– полное сопротивление цепи или импеданс, тогда

Z= (16)

Из рис. 11 получаем

tg = (17)

Закон Ома для рассматриваемой цепи будет иметь вид:

J_{max =} (18)

Электроизмерительные приборы показывают не амплитудные значения тока и напряжения, а эффективные, которые связаны между собой следующим образом:

I_эф = U_эф=,

Тогда выражение /18/ примет вид:

/19/