ответы к экзамену / пацантрэ / 1-25 / 24Симметрирование ВТ

Вторичное симметрирование. Для уменьшения погрешности выходного напряжения, снимаемого с синусной обмотки, подключают к косинусной обмотке сопротивление Z_нС (рис. 5.27, а). В этом случае ток, проходящий по обмотке С, создает МДС F_С , которую можно представить, так же как и МДС F_S , в виде векторной суммы двух составляющих (рис. 5.27,б): продольной F_Сd = F_С cos θ и поперечной F_Cq = F_С sin θ. Продольная составляющая F_Cd совпадает по направлению с F_Sd , a поперечная составляющая F_Cq направлена против F_Sq . При F_Cq = F_Sqпоперечный поток Ф_q = 0. Следовательно, не возникает и погрешность, обусловленная этим потоком. Сопротивление Z_нС, при котором обеспечено полное симметрирование, можно определить из условия

(5.53)

F_S cos θ = F_C sin θ

или с учетом значений F_S и F_C

(5.54)

Z_S + Z_нS = Z_C + Z_нC ,

т. е. полное симметрирование наблюдается при равенстве комплексных сопротивлений в цепи обмоток S и С ротора, т. е. их активных и реактивных составляющих. При вторичном симметрировании компенсируются МДС по поперечной оси; кроме того, ток I_в в обмотке возбуждения поворотного трансформатора не зависит от угла поворота, так как в формулу для результирующей продольной составляющей МДС ротора F́_2d = F́_Sd + F́_Cd (определяющей силу тока I_в) не входит какаялибо функция угла θ:

F́2d = F́S sin θ + F́C cos θ =

0,9kÉв w2 kоб2 sin θ ZS + ZнC

sin θ +

0,9kÉв w2 kоб2 cos θ ZC + ZнC

cos θ =

0,9kw2 kоб2 Z2 + Zн

Éв ,

где Z₂ = Z_S = Z_C ; Z_н = Z_нS = Z_нC .

В результате уменьшается погрешность поворотного трансформатора.

Рассмотренный метод симметрирования практически применим только при постоянном сопротивлении нагрузки, что является его недостатком.

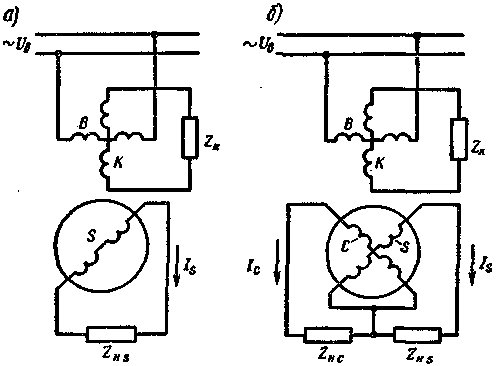
Первичное симметрирование. Для уменьшения погрешности выходного напряжения снимаемого, например, с обмотки S (рис. 5.28, а), компенсационную обмотку К статора замыкают на какое-либо малое сопротивление Z_K или накоротко. В этом случае по поперечной оси вращающегося трансформатора действует результирующая МДС

(5.55)

F_q = F_Sq + F_K ,

где F_K — МДС, создаваемая компенсационной обмоткой.

Так как обмотка К относительно поперечного потока Ф_q представляет собой замкнутую накоротко вторичную обмотку трансформатора, то ее МДС F́_K направлена против МДС F́_Sq«первичной» обмотки, и результирующая МДС F_q , так   же   как   и   в   трансформаторе   тока, значительно

Рис, 5.28. Схемы синусно-косинусных вращающихся трансформаторов

меньше МДС F_Sq . Поэтому поперечный поток Ф_q и вызванная им погрешность резко уменьшаются. При изменении нагрузки, подключенной к обмотке ротора, МДС F_K изменяется примерно пропорционально МДС F_Sq , вследствие чего степень компенсации поперечного потока остается практически неизменной. Это является достоинством данного метода симметрирования. Однако при изменении угла поворота ротора θ изменяется ток I_в в обмотке возбуждения и при заданном напряжении Ú_в изменяется ЭДС É_в . В результате появляется дополнительная погрешность в значении выходных напряжений Ú_S и Ú_C на зажимах синусной и косинусной обмоток. Поэтому во вращающихся трансформаторах обычно применяют одновременно первичное и вторичное симметрирование (рис. 5.28,б). Рассмотренные методы компенсации поперечного потока Ф_q позволяют использовать в качестве выходной как синусную, так и косинусную обмотки. Поэтому вращающийся трансформатор, включенный по схеме, изображенной на рис. 5.28,б, называют синусно-косинусным.