REL исходный с п

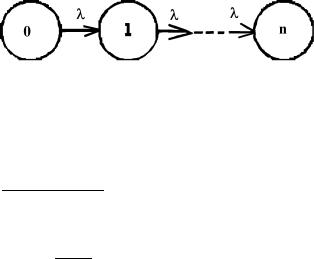
61

Рис. 5.3. Размеченный граф переходов для невосстанавливаемой системы n-кратного ненагруженного резервирования

.

Преобразуем соотношение (5.5) к виду

pk (t + ) pk (t) = k 1; pk 1(t) k pk (t) + o(1);

откуда, переходя к пределу при ! 0, найдем

Заметим, что размеченный граф переходов позволяет сразу выписать дифференциальные уравнения для вероятностей состояний марковского процесса с помощью следующего правила:

Производная вероятности некоторого состояния равна алгебра- ической сумме произведений вероятностей состояний на интенсивности переходов, взятых со знаком + для входящих в это состояние стрелочек и со знаком для выходящих из него.

Если в начальный момент все элементы работоспособны, то, решая систему (5.6) с начальными условиями

для системы ненагруженного резервирования без восстановления найдем функцию надежности в виде

62

Для нагруженного резервирования и в случаях более общего резервирования, когда имеется несколько основных и несколько резервных элементов формулы получаются достаточно громоздкими, их можно найти, например, в Справочнике [5].

5.5Свойства надежности резервированных систем

Рассмотрим некоторые свойства надежности резервированных систем.

5.5.1 Зависимость надежности от уровня резервирования

Рассмотрим вопрос о влиянии уровня резервирования на надежность системы. На рис. 5.4 и 5.5 приведены две схемы резервирования, более высокого и более низкого уровня резервирования:

..

При параллельно-последовательном соединении элементов, представленном на рис. 5.4, структурные функции последовательных ча- стей равны соответственно,

f1(x1; x2) = x1x2; f2(x3; x4) = x3x4;

отсюда структурная функция fI системы, представленной на рис. 5.4, равна

fI = 1 (1 f1(x1; x2))(1 f2(x3; x4)) = 1 (1 x1x2)(1 x3x4):

63

Ïðè pi = p для вероятности безотказной работы системы получим выражение

Аналогичные рассуждения для второй системы, представленной на рис. 5.5, дают

fII = f1(x1; x2)f2(x3; x4) = (1 (1 x1)(1 x3))(1 (1 x2)(1 x4)):

Откуда

Графики функций hI (p) è hII (p), приведенные на рис. 5.6, показывают, что уменьшение уровня резервирования увеличивает надежность системы.

Аналогичная картина имеет место при увеличении числа элементов системы. Пусть система состоит из k последовательно соединенных в смысле надежности элементов, и обозначим ее надежность

через p. Если составляющие ее элементы равнонадежны, то величи- p

íà k p представляет собой надежность каждого из ее элементов. При дублировании элементов системы ее надежность имеет вид

Рис. 5.6. Графики зависимости надежности системы от надежности ее элементов при различных уровнях резервирования

.

64

Откуда для достаточно высоконадежных элементов p = 1 , рас-

p

кладывая выражение k 1 (1 p) в ряд Тейлора, найдем

Последнее соотношение позволяет сделать вывод, что если система состоит из большого числа достаточно надежных элементов, то можно добиться сколь угодно близкой к 1 надежности. Заметим также, что приведенные выше рассуждения применимы также для оценок надежности систем во времени.

5.5.2 При резервировании увеличивается надежность системы из достаточно надежных элементов

Справедлива

Теорема. Зависимость надежности монотонной структуры от надежности ее элементов имеет S-образную форму. |

Продемонстрируем утверждение теоремы на примере: Пример. Рассмотрим систему из 3-х равнонадежных элементов,

представленную на рис. 5.7.

Рис. 5.7 Система из трех элементов

.

Функция надежности h(p) этой системы равна

65

где p - надежность отдельного элемента.

Рассмотрим 2 варианта резервирования системы: 1-й вариант дублирование системы в целом. В этом случае функция надежности системы равна:

hI (p) = 1 [1 (p2(2 p))]2 = p2(2 p)(2 p2(2 p)); (13)

2-й вариант дублирование по элементам. В этом случае функция надежности системы имеет вид:

hII (p) = [2p p2][1 (1 p)4] = p2(2 p)2(2 p(2 p)): (14)

Графики вероятностей безотказной работы этих систем в зависимости от надежности их элементов аналогичны представленным на рис. 5.6 и имеют S-образный вид, который показывает, что при любом способе резервирования надежность системы из достаточно надежных элементов увеличивается, хотя резервирование ненадежными элементами может уменьшить надежность системы.

5.5.3 Объединение резерва увеличивает надежность

Рассмотрим 2 варианта резервирования системы, состоящей из k элементов индивидуальное (раздельное) и общее (объединенное) резервирование k резервных элементов. Эти два способа резервирования показаны на рис. 5.8 и 5.9.

Нетрудно вычислить среднее время до отказа системы при этих двух способах резервирования.

1) При общем резервировании с показательным законом надежности элементов, т.к. элементы подсоединяются по мере отказа и отказ системы происходит в момент k-го отказа (пока не кончатся k запасных деталей), среднее время до отказа системы îáù. равно

66

Рис. 5.8. Раздельное резервирование

где k суммарная интенсивность отказов элементов.

2) В случае раздельного (индивидуального) резервирования можно показать, что среднее время до отказа системы : равно

Для сравнения этих способов резервирования обозначим через

Ниже приведены значения коэффициента эффективности резервирования для k = 1; 2; 3: W1 = 1; W2 = 1:2; W3 = 1:38: Можно

67

показать, что с ростом числа элементов k, коэффициент эффективности общего резервирования по отношению к раздельному растет,

5.5.4 Резервирование невосстанавливаемых систем увеличи- вает их надежность не более чем линейно (по числу элементов)

Предположим, что для повышения надежности изделия имеется резерв из k аналогичных изделий. Тогда в лучшем случае ненагруженного резерва среднее время работы всей системы Tf будет равно сумме длительностей работы резервных изделий,

1 i n

при этом среднее время работы системы имеет вид

что показывает линейность роста среднего времени работы системы.

5.6Примеры. Упражнения

Упражнения ([6], стр. 136, см. также упр. предыдущего параграфа).

1. Схема расчета надежности приведена на рис. 5.10. Интенсивности отказов элементов постоянны и имеют следующие значения:1 = 0; 3 10 3 (1=), 2 = 0; 7 10 3 (1=). Вычислить функции надежности, частоту и опасность отказа системы и определить вероятность безотказной работы изделия в течении времени t = 100 часов, среднюю наработку на отказ, частоту отказов и опасность отказов в момент времени t = 100 часов.

68

Рис. 5.10. Схема расчета надежности к упражнению 1.

Ответ:

4 (1/÷àñ.);

c(100) = Pa(100)(100) 1; 8 10 4 (1/÷àñ.):

2. Схема расчета надежности приведена на рис. 5.10. Вычислить функции надежности, частоту и опасность отказа системы и определить вероятность безотказной работы изделия в течении времени t = 100 часов, среднюю наработку до первого отказа, частоту отказов и опасность отказов в момент времени t = 100 часов, если интенсивности отказов элементов постоянны и имеют следующие значения: 1 = 0; 3 10 3(1/÷àñ.); 2 = 0; 7 10 3(1/÷àñ.).

Ответ:

69

3. ([6], стр. 141). Двигатель автомобиля имеет 4 свечи зажигания, по одной на каждый цилиндр. Интенсивность отказов свечи= 10 3(1=:). Предполагается, что автомобиль может ехать также при одном неработающем цилиндре. Вычислить функцию надежности работы двигателя и определить вероятность того, что путешествие длительностью t = 20(:) закончится благополучно (без замены свечей).

Ответ:

Rf (t) = 4e 3 t 3e 4 t; Rf (20) = 0; 9977:

70

Ÿ6 Резервирование с восстановлением.

6.1Описание модели.

Рассмотрим теперь резервированную систему в предположении, что отказавшие элементы могут восстанавливаться. Относительно способа резервирования сохраняются прежние предположения, т.е. резерв может быть нагруженным, ненагруженным или облегченным. Относительно числа ремонтных бригад (числа одновременно ремонтируемых элементов) также возможны различные предположения: доступно лишь одно ремонтное устройство (бригада), возможен одновременный ремонт всех отказавших элементов или имеется ограни- ченное число ремонтных устройств. Мы подробно рассмотрим только одну из возможных ситуаций (облегченного дублирования с одной ремонтной бригадой), на которой будет продемонстрирована методика расчета надежности таких систем, предлагая рассмотреть другие в качестве самостоятельных упражнений. Отказавшее устройство поступает на ремонт и после ремонта возвращается обратно в резерв.

Предположим, что длительности Tn; Tnðåç. безотказной работы основного и резервного элементов, а также длительности восстановления Tn0 элементов имеют показательные распределения,

F (t) = PfTn < tg = 1 e t;

со средними значениями T = 1; T ðåç. = 1; T 0 = 1 соответственно.

Для построения математической модели рассматриваемого явления обозначим через X(t) число элементов, находящихся в состоянии отказа в момент времени t. При сделанных предположениях процесс X(t) оказывается марковским, т.е. процессом, поведение которого в будущем не зависит от его прошлого поведения при известном настоящем. Это свойство процесса следует из леммы разд. 1.3.1. об отсутствии памяти у показательного распределения. Как уже отмечалось