(35)84.Что такое прямоугольные и квадратные матрицы? Примеры.

Матрицей называется прямоугольная таблица чисел, состоящая из m одинаковой длины строк или n одинаковой длины столбцов.

aij- элемент матрицы, который находится в i-ой строке и j-м столбце.

Для краткости матрицу можно обозначать одной заглавной буквой, например, А или В.

В общем виде матрицу размером m×n записывают так

.

Примеры:

Если в матрице число строк равно числу столбцов, то матрица называется квадратной, причём число ее строк или столбцов называется порядком матрицы. В приведённых выше примерах квадратными являются вторая матрица – её порядок равен 3, и четвёртая матрица – её порядок 1.

Матрица, в которой число строк не равно числу столбцов, называется прямоугольной. В примерах это первая матрица и третья.

Главной диагональю квадратной матрицы назовём диагональ, идущую из левого верхнего в правый нижний угол.

Квадратная матрица, у которой все элементы, лежащие ниже главной диагонали, равны нулю, называется треугольной матрицей.

.

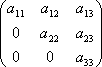Квадратная матрица, у которой все элементы, кроме, быть может, стоящих на главной диагонали, равны нулю, называется диагональной матрицей. Например, или .

Диагональная матрица, у которой все диагональные элементы равны единице, называется единичной матрицей и обозначается буквой E. Например, единичная матрица 3-го порядка имеет вид .

↑ назад в содержание ↑

(36)85.Что такое линейные операции над матрицами? Примеры.

Во всех случаях, когда вводятся новые математические объекты, необходимо договариваться о правилах действийнад ними, а также определить - какие объекты считаются равнымимежду собой.

Природа объектов не имеет никакого значения. Это могут быть вещественные или комплексные числа, векторы, матрицы, строки или что-то иное.

К числу стандартных действий относятся линейные операции, а именно: умножение на число и сложение; в данном конкретном случае - умножкние матрицы на число и сложение матриц.

При умножении матрицы на число каждый матричный элемент умножается на это число, а сложение матриц подразумевает попарное сложение элементов, расположенных в эквивалентных позициях.

Терминологическое выражение " линейная комбинация<" (векторов, матриц, строк, столбцов и так далее) всегда означает одно и тоже: алгебраическая сумма этих векторов (или матриц, строк, столбцов и так далее), предварительно умноженных на числовые коэффициенты.

Матрицы  A = || a_i j ||  и  B = || a_i j ||  считаются равными, если они имеют одинаковые размеры и их соответствующие матричные элементы попарно равны:

(1)

для любых допустимых значений индексов  i  и  j.  К линейным операциям над элементами множества или пространства относятся операции сложения элементов и их умножения на скаляр (число).  Умножение матрицы на число  При умножении матрицы  A  на число  λ  (слева или справа) каждый ее матричный элемент умножается на это число:

(2)

Сложение матриц  Операция сложения определена только для матриц одинаковых размеров. Результатом сложения матриц  A = || a_i j ||  и  B = || b_i j ||  является матрица  C = || c_i j || , элементы которой равны сумме соответствующих матричных элементов:

(3)

Линейной комбинацией матриц A и B называется выражение вида  , гдеи– числовые коэффициенты.

↑ назад в содержание ↑