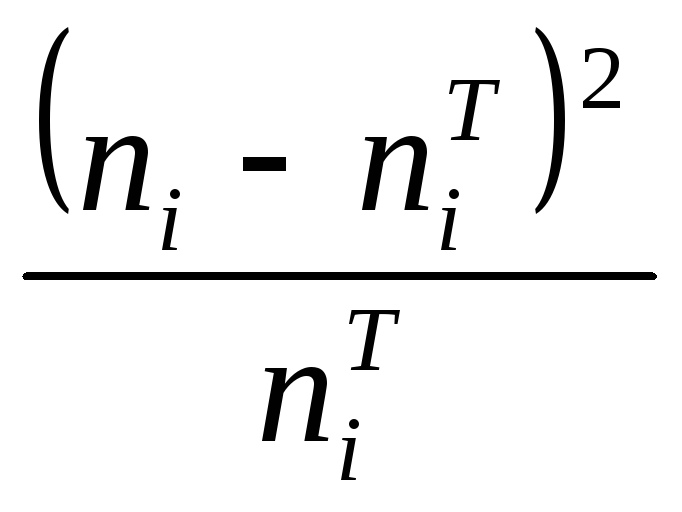4 Проверка гипотезы о нормальном законе распределения:

4.1 По критерию Пирсона:

D*(X) = 1029;=32,093; n= 1000; = 84,53;=0,05

Н₀:X ~ N(84,53; 32,093)

Н₁:X ~ N(84,53; 32,093)

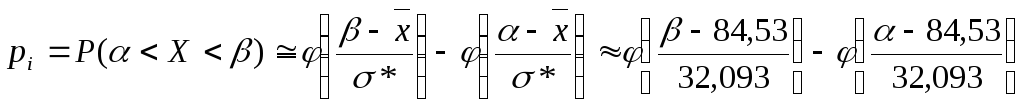
= -0,3577+0,4678=0,1101

= -0,1141+0,3577=0,2436

= -0,1844+0,1141=-0,0703

= -0,3969+0,1844=-0,2125

= 0,4793+0,3969=0,8762

= 0,4975+0,4793=0,9768

Вспомогательная таблица для расчёта критерия Пирсона

№ i- ин- тер вала	Интервал Δ [α÷β]	Эмпириче- ские частоты		Вероятность попадания в i-интервал	Теоретичес- кие частоты			Эмпирическая плотность распределения вероятностей
1	25-50	201	510	0,1101	11,01	35,37	6369,06	0,002
2	50-75	309		0,2436	24,36			0,004
3	75-100	174		-0,0703	-7,03		-4661,71	-0,001
4	100-125	126		-0,2125	-21,25		-1020,35	-0,004
5	125-150	100		0,8762	87,62		1,74	0,017
6	150-175	90		0,9768	97,68		0,60	0,019
∑		1000		1,9239	192,39		=689,34	----

Порядок проверки нулевой гипотезы:

1)=689,34

2)

3) <принимаемН₀ ,отвергаемН₁

Вывод: С вероятностью 0,95 можно утверждать, что случайная величинаХ имеет нормальный закон распределения с параметрамиN(84,53; 32,093)

Построение нормальной кривой по опытным данным:

1) Определяем значения . В нашем примере ширина интервала= 5 мкм, а объём выборки

n = 1000 . Тогда получим:.

Значения приведены в вспомогательной таблице в последнем столбце.

2) Определяем «»-интервал:

у.е..

3) Нормальная кривая симметрична относительно прямой

у.е.

4) Максимум нормальной кривой находится в точке

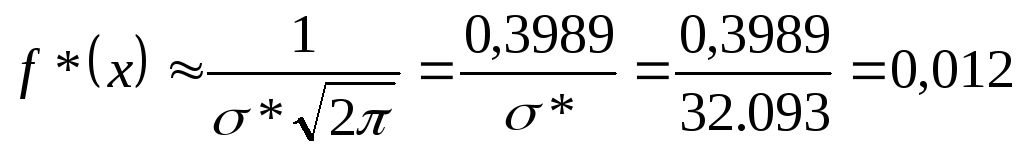
4.2 По критерию Колмогорова:

D*(X) = 1029,97(у.е)²;= 32,093 у.е; n= 1000; = 84,53;=0,05

Н₀:X ~ N(84,53; 32,093)

Н₁:X ~ N(84,53; 32,093)

Группированный статистический ряд, статистическое распределение частот, относительных частот, накопленных частот и частостей.

№ интер- вала	1	2	3	4	5	6
∆хi, мкм	25-50	50-75	75-100	100-125	125-150	150-175
ni	201	309	174	126	100	90
Wi	0,201	0,309	0,174	0,126	0,1	0,09
nнак	201	510	684	810	910	1000
Wнак	0,201	0,51	0,684	0,81	0,91	1

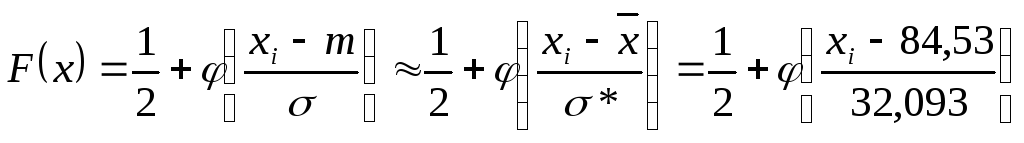
Значения эмпирической и теоретической функций распределения.

, мкм	25	50	-75	100	125	150	175
	0	2,01	5,1	6,84	8,1	9,1	10
	0,312	0,142	0,385	0,684	0,896	0,979	0,997
	0,312	1,868	4,715	6,116	7,204	8,121	9,003

Максимальное значение абсолютной величины разности между эмпирической и теоретической функциями распределения:

Порядок проверки нулевой гипотезы:

1)

2)

3) ОтвергаемН₀ ,принимаемН₁..

Вывод: С вероятностью 0,95 можно утверждать, что случайная величинаХ имеет нормальный закон распределения с параметрамиN(84,53; 32,093)