По данным выборочного обследования получено следующее распределение семей по среднедушевому доходу.

доход, у.е.	25÷ 50	50÷ 75	75÷ 100	100÷ 125	125÷ 150	150 ÷175
Количество семей	201	309	174	126	100	90

Провести первичную статистическую обработку экспериментальных данных.

РЕШЕНИЕ:

1)Составим статистическое распределениечастотn_i, относительных частотW_i, накопленных частотn_наки накопленных частостейW_нак

Для каждого интервала указывается частота n_i, относительная частотаW_i=n_i/n, накопленная частотаn_нак(находится последовательным суммированием частот всех предыдущих интервалов) и накопленная частостьW_нак=n_нак/n.

Группированный статистический ряд, статистическое распределение частот, относительных частот, накопленных частот и накопленных частостей

№ интер- вала	1	2	3	4	5	6
∆хi, мкм	25÷ 50	50÷ 75	75÷ 100	100÷ 125	125÷ 150	150 ÷175
ni	201	309	174	126	100	90
Wi	0,201	0,309	0,174	0,126	0,1	0,09
nнак	201	510	684	810	910	1000
Wнак	0,201	0,51	0,684	0,81	0,91	1

2)Построим гистограммучастот в координатах (x_i, n_i) и относительных частот в координатах (x_i, W_i) (рис. 1.1). Если соединить середины интервалов, получимполигончастот и относительных частот.

Рис.1.1. Гистограмма и полигон частот и относительных частот

3)Построим кумуляту. (рис.1.2).

Рис. 1.2. Кумулята

4)Найдем эмпирическую (выборочную) функцию распределенияF*(x). построим график эмпирической функции распределения (рис.1.3).

xi у.е.	25	50	75	100	125	150	175
F*(x)	0	0,201	0,510	0,684	0,810	0,910	1,0

Рис. 1.3. График эмпирической функции распределения

Для облегчения вычислений выборочных числовых характеристик составим табл. 1.3.

Таблица 1.3

Вспомогательная таблица для вычисления числовых характеристик

№	Середина интервала хi у.е.	ni	xi ni	xi-	(xi -)2ni	(xi - )3ni	(xi - )4ni
1	37,5	201	7537,5	-47,0323	444619,4859	-20899074,615	982931547,0541
2	62,5	309	19219,8	-22,0323	149995,4731	-3304745,2636	72811139,0579
3	87,5	174	15225	2,9677	1532,46033	4547,8825	13496,75089
4	112,5	126	14175	27,9677	98556,2226	18724226,6924	52367468,005
5	137,5	100	13750	52,9677	280557,7243	14860497,3749	787126366,8044
6	162,5	90	14625	77,9677	547106,6018	42656643,4046	3325840375,93005
∑	-	1000	84532,3	-	10299977,9712	52040995,47497	5221090393,602

Определим выборочные числовые характеристики:

Выборочное среднее:

Выборочная дисперсия:

Выборочное среднее квадратическое отклонение:

Выборочная мода Мо* = 87,5 у.е.;

Выборочную медиану Ме* = 87,5 у.е.

Коэффициент вариации:

Так как коэффициент вариации больше 33%, то выборка неоднородна.

Выборочный коэффициент ассиметрии:

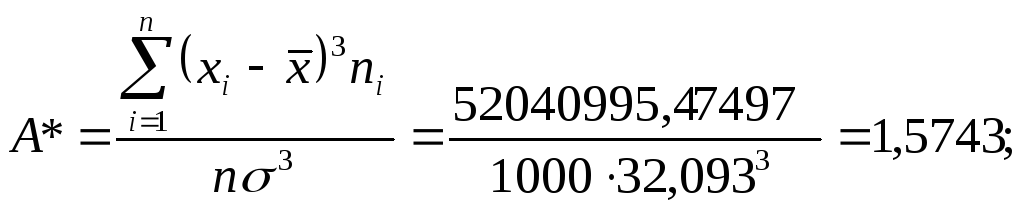
Выборочный эксцесс Е*и коэффициент эксцесса*:

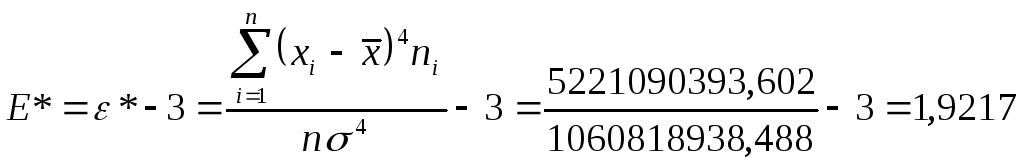
Приблизительная проверка нормальности распределения:

По виду гистограммы и полигона можно считать распределение симметричным.

Так как , то распределение можно считать приблизительно нормальным.

Так как Е*0 иА*0, то распределение можно считать приблизительно нормальным.

Найдем трехсигмовый интервал:

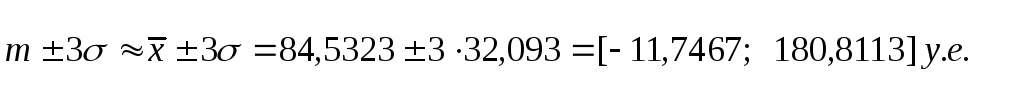
Все значения случайной величины попали в трехсигмовый интервал, поэтому распределение можно считать приблизительно нормальным.

Так как выборочное распределение можно считать нормальным, найдем доверительный интервал для математического ожиданияМ(Х)=mпри уровне надежности=0,95 по следующей формуле:

По таблице функции Лапласа найдем:

Ф(z_)= 0,95/2=0,475 иz_= 1,96.

Найдем предельную ошибку выборки:

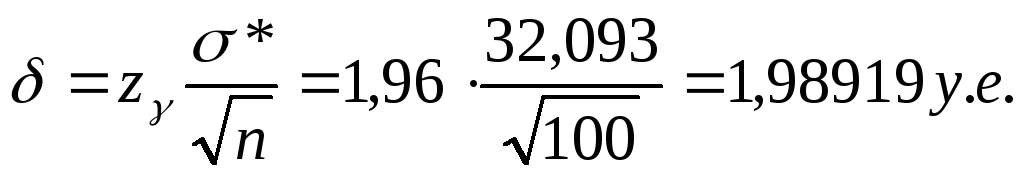
Найдем доверительный интервал:

84,5323-1,98919 m 84,5323+1,98919;

82,54311m 86,52149.

С заданной надежностью (вероятностью) 0,95 можно ожидать, что отклонение размера деталей от номинального находится в интервале от -0,09487 до 3,49487 у.е.

^{ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ}

Государственное образовательное учреждение

высшего профессионального образования

^{«МАТИ»  РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ ИМЕНИ К.Э. ЦИОЛКОВСКОГО}

^{Кафедра «Моделирование систем и информационные технологии»}

Индивидуальное задание по теме: «первичная статистическая обработка экспериментальных данных»

^{Студент: Грачева А.С.}

^{Группа: АСУ - 031}

^{Преподаватель: Егорова Ю. Б.}