
Контрольная работа 2 вариант 3
.pdfБанк рефератов Vzfeiinfo.Ru
Соглашение об использовании
Материалы данного файла могут быть использованы без ограничений для написания собственных работ с целью последующей сдачи в учебных заведениях.
Во всех остальных случаях полное или частичное воспроизведение, размножение или распространение материалов данного файла допускается только с письменного разрешения администрации проекта http://www.vzfeiinfo.ru/.
1
Вариант 3
Контрольная работа № 2
1.Найти неопределенный интеграл:
∫3x (2x −5)dx .
Решение.
Для вычисления этого интеграла воспользуемся методом интегрирования по частям:
∫3x (2x −5)dx = |
|
u = 2x −5 |
|
du = 2dx |
|
=(2x −5) |
3x |
−∫ |
3x |
2dx = |
|
||||||||||||||
|
|
|
|
||||||||||||||||||||||
|
|
|
3x |
|
|
|
|||||||||||||||||||
|
dv =3x dx v = |
|
|
ln 3 |
ln 3 |
|
|||||||||||||||||||
ln 3 |
|
||||||||||||||||||||||||
=(2x −5) |
3x |
2 |
∫3 |
x |
|
|
(2x −5)3x |
|
2 3x |
(2x −5)3x |
2 3x |
||||||||||||||
|
− |
|
|
dx |
= |
ln 3 |
|
|
− |
|
|
|
+C = |
|
ln 3 |
− ln2 3 +C; |
|||||||||
ln 3 |
ln 3 |
|
|
|
ln 3 |
ln 3 |
|
||||||||||||||||||
2. Вычислить определенный интеграл:
e |
dx |
||
∫1 |
|||
|
. |
||
x(ln2 x −5ln x +6) |
|||
Решение.
Вычислим интеграл, используя метод замены переменной:
|
|
|
ln x =t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
dx |
|
dx = dt |
1 |
dx |
1 |
dt |
|
∫1 |
|
= |
t x=ln1 =0 |
= ∫0 |
|
= ∫0 |
|
; |
x(ln2 x −5ln x +6) |
t2 −5t +6 |
(t −3)(t −2) |
||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
t2 =ln e =1 |
|
|
|
|
|
Воспользуемся методом неопределенных коэффициентов для разложения подынтегральной функции на простейшие дроби I типа.
2

1 |
= |
1 |
= |
A |
+ |
B |
; |
t2 −5x +6 |
(t −3)(t −2) |
t −3 |
t −2 |
Приведем в правой части дроби к общему знаменателю и освободимся от знаменателя.
1 = A( t −2 ) + B(t −3);
Сгруппируем члены с одинаковыми степенями:
1 =( A + B )t −2A −3B ;
Сравнивая коэффициенты при одинаковых степенях x, получаем систему уравнений:
A + B = 0 |
, из которой найдем коэффициенты A =1, B = −1. |
|
|
−2 A −3B =1 |
|
Итак, разложение рациональной дроби на простейшие имеет вид:
|
|
|
|
1 |
|
|
|
|
|
= |
|
|
1 |
|
|
− |
1 |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
t2 −5t +6 |
|
t −3 |
t −2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Таким образом, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
1 |
|
|
|
|
dx |
|
|
|
|
1 |
|
1 |
|
|
|
1 |
|
|
=(ln |
|
|
|
) |
|
1 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
dx |
t −3 |
−ln |
t −2 |
|
|
= |
||||
|
∫0 t |
2 |
|
|
|
|
|
|
|
|
|
|
∫0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
−5t +6 |
|
|
|
t − |
3 |
|
t − |
2 |
|
|
|
|
|
|
|
0 |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
=ln |
|
|
t −3 |
|
|
|
|
1 |
= ln |
|
2 |
|
|
−ln |
|
3 |
|
|
|
=ln |
4 |
≈0,29. |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
t −2 |
|
|
|
|
|
1 |
|
|
|
2 |
|
|
3 |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Ответ: ln 43 ≈0,29.
3.Вычислить определенный интеграл:
∫1 e x dx.
0
Решение.
Воспользуемся методом замены переменной, и затем, проинтегрируем по частям:
3

|
x =t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
x =t2 |
|
1 |
|
u =t du = dt |
|
|
1 |
1 |
1 |
|
1 |
|||
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
||||||||||
∫e x dx = |
dx = 2tdt |
= 2∫ettdt = |
|
t |
dt v =e |
t |
=ett |
|
− ∫et dt =ett |
|
0 |
−et |
|
0 = |
|
|
0 |
|
|
||||||||||||
0 |
t1 = |
0 =0 |
0 |
|
dv =e |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
t2 = |
1 =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
=e −0 −e +e0 =1.
Ответ: 1.
4. Решить дифференциальное уравнение: 2 y′−3y =e3x .
Решение.
2 y′−3y = e3x ;
2 dydx −3y =e3x ;
Это линейное уравнение первого порядка.
Пусть y =uv , тогда |
dy |
=u dv |
+v du . |
|
dx |
dx |
dx |
Подставляя выражение dydx в исходное уравнение, будем иметь:
2u dvdx +2v dudx −3uv =e3x ;
|
2 |
dv |
|
+ 2v |
du |
=e |
3x |
; (1) |
u |
dx |
−3v |
dx |
|
||||
|
|
|
|
|
|
|
Для определения v получим уравнение
2 dvdx −3v =0;
4
т.е. 2 dvdx =3v;
dvv = 32 dx;
∫dvv = 32 ∫dx;
Получили
lnv = 32 x (постоянную интегрирования не вводим, так как достаточно найти ка-
кое-либо частное решение этого вспомогательного уравнения).
3x
v= e2 ;
Подставляя выражение функции v в уравнение (1), получаем для определения u уравнение
2e32 x dudx =e3x
или du = |
1 e23 xdx, |
|
2 |
∫du = 12 ∫e32 xdx,
откуда u = 13 e32 x +C;
Следовательно, общее решение заданного уравнения будет иметь вид
|
1 |
3 x |
|
3 x |
= |
1 |
e |
3x |
3 x |
. |
y =uv = |
3 |
e2 |
+C e2 |
3 |
|
+Ce2 |
||||
|
|
|
|
|
|
|
|
|
||
5. Вычислить площадь фигуры, ограниченной линиями:
y = x3 , |
y = x2 , |
x = −2, x =1. |
5

Решение.
Построим графики функций:
|
y |
4 |
y = x2 |
|
y = x3 |
3
2
1
x
-4 |
-3 |
-2 |
-1 |
1 |
2 |
3 |
4 |
5 |
-1
-2
1 |
|
2 |
|
3 |
x3 |
|
x4 |
|
1 |
|
1 |
|
1 |
|
8 |
|
|
|
1 |
|
1 |
|
8 |
|
3 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
S = ∫ |
(x |
|
− x |
|
)dx = |
|
− |
|
|
|
|
= |
|
− |
|
− |
− |
|
−4 |
|
= |
|
− |
|
+ |
|
+4 =6 |
|
. |
|
|
3 |
4 |
3 |
3 |
3 |
4 |
3 |
4 |
||||||||||||||||||||
−2 |
|
|
|
|
|
|
|
|
−2 |
|
|
4 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
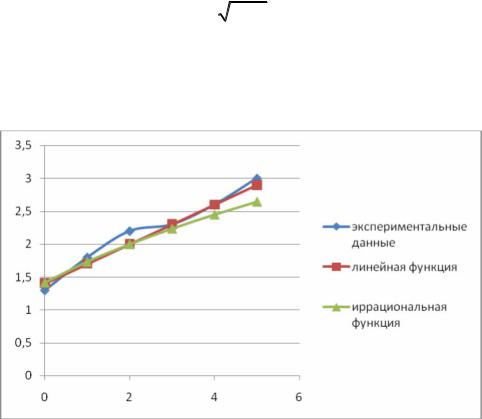
6.Экспериментальные данные о значениях переменных x и y приведены в таблице:
|
xi |
0 |
1 |
2 |
3 |
|
4 |
5 |
|
|
|
|
|
|
|
|
|
|
yi |
1,3 |
1,8 |
2,2 |
2,3 |
|
2,6 |
3 |
|
|
|
|
|
|
|
|
|
В результате их выравнивания получена функция y = |
x + 2 . Используя метод |
|||||||
наименьших квадратов, аппроксимировать эти данные линейной зависимостью
6

y = ax +b (найти параметры a и b). Выяснить, какая из двух линий лучше (в смысле метода наименьших квадратов) выравнивает экспериментальные данные. Сделать чертеж.
Решение.
Для определения коэффициентов линейной зависимости используют формулы:
a∑n |
xi2 +b∑n |
xi =∑n |
xi yi , |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
i=1 |
|
i=1 |
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
n |
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
a∑xi +nb =∑yi . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
i=1 |
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Построим и заполним вспомогательную таблицу: |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
x |
|
|
y |
|
x2 |
x y |
y* |
y% |
|
* − |
yi ) |
2 |
% |
− |
yi ) |
2 |
|
|
i |
|
|
i |
|
i |
i i |
i |
i |
|
(yi |
|
(yi |
|
|
|||
|
1 |
|
0 |
|
|
1,3 |
|
0 |
0 |
1,4 |
1,41 |
|
|
0,01 |
|
|
0,01 |
||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
2 |
|
1 |
|
|
1,8 |
|
1 |
1,8 |
1,7 |
1,73 |
|
|
0,01 |
|
|
0,00 |
||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
3 |
|
2 |
|
|
2,2 |
|
4 |
4,4 |
2 |
2,00 |
|
|
0,04 |
|
|
0,04 |
||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
4 |
|
3 |
|
|
2,3 |
|
9 |
6,9 |
2,3 |
2,24 |
|
|
0,00 |
|
|
0,00 |
||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
5 |
|
4 |
|
|
2,6 |
|
16 |
10,4 |
2,6 |
2,45 |
|
|
0,00 |
|
|
0,02 |
||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
6 |
|
5 |
|
|
3 |
|
25 |
15 |
2,9 |
2,65 |
|
|
0,01 |
|
|
0,13 |
||
|
|
|
|
|
|
|
|
|
|
||||||||||
∑ |
|
15 |
|
13,2 |
|
55 |
38,5 |
12,9 |
12,48 |
|
|
0,07 |
|
|
0,21 |
||||
7
Используя полученные значения, имеем:
55a +15b =38,5,15a +6b =13,2.
Решая систему, получаем:
a =0,3; |
b =1,4. |
Т.е. y =0,3x +1,4.
Дополним таблицу для определения, какая из линий лучше (в смысле наименьших квадратов), выравнивает экспериментальные данные, обозначив значения, полученные по формуле
y = 0,3x +1,4 : y*; |
y = x + 2 : y. |
|
% |
Т.к. min{0,07;0, 21} = 0, 21,
то делаем вывод, что прямая лучше выравнивает экспериментальные данные.
7.Используя разложение функции y =ln(1 + x) в степенной ряд, вычислить ln1,12 с точностью до 0,001.
Решение.
8
Для вычисления ln1,12 запишем ряд ln(1 + x) = x − |
x2 |
+ |
x3 |
−K |
(−1)n xn+1 |
+K при |
||||
2 |
3 |
n +1 |
||||||||
x =0,12, входящем в область сходимости |
(−1;1]: |
|
|
|
||||||
|
|
|
|
|
|
|||||
ln1,12 =0,12 − 0,122 |
+ 0,123 |
−K(−1)n 0,12n+1 |
+K= |
|
|
|
|
|
|
|
2 |
3 |
n +1 |
|
|
|
|
|
|
|
|
=0,12 −0,0072 +0,000576 −0,00005184 +K
Если в качестве ln1,12 взять первых два члена, то мы допускаем погрешность
|
r |
|
= |
0,123 |
+ |
0,124 |
+K+ |
0,12n |
0,123 |
+ |
0,125 |
+K+ |
0,12n |
+K= |
|||||||
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
+K< |
|
|
|
||||||||||
|
n |
|
|
|
|
3 |
|
4 |
|
|
n |
|
3 |
|
|
3 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
= |
0,123 |
(1 +0,12 +K+0,12 |
n−3 |
+K)= |
0,123 |
|
|
1 |
|
=0,000655 <0,001 |
|||||||||||
3 |
|
|
3 |
1 −0,12 |
|||||||||||||||||
Итак,
ln1,12 ≈ 0,12 −0,0072 = 0,1128 ≈ 0,113.
9
