
- •1. Марковские процессы. Основные понятия
- •1.1 Случайные процессы и их классификация
- •1.2 Марковское свойство и его следствия
- •1.3 Финальные вероятности
- •1.4 Дискретные марковские процессы с непрерывным временем
- •2 Ветвящиеся процессы. Основные понятия
- •2.1 Ветвящиеся процессы и их классификация
- •2.2 Предельные теоремы для распределения числа частиц в ветвящихся процессах
- •2.3 Марковские ветвящиеся процессы с непрерывным временем
- •3. Исследование развития эпидемиологического заболевания
- •3.1 Использование математических методов в эпидемиологии
- •3.2 Исследование заболеваемости туберкулезом с использованием марковских цепей с непрерывным временем
- •3.3 Результаты исследования
2.2 Предельные теоремы для распределения числа частиц в ветвящихся процессах
Мы
знаем, что математическое ожидание
числа частиц n-го
поколения в надкритических процессах
Гальтона–Ватсона растет как
 ,
причем коэффициент вариации
,
причем коэффициент вариации стабилизируется при стремлении
стабилизируется при стремлении к бесконечности:
к бесконечности:

Это
позволяет надеяться на то, что и размер
популяции
 в моментn,
нормированный математическим ожиданием
в моментn,
нормированный математическим ожиданием
 ,
также будет в определенном смысле
сходиться при
,
также будет в определенном смысле
сходиться при к некоторой случайной величине. Результаты
данного раздела подтверждают эту
гипотезу.
к некоторой случайной величине. Результаты
данного раздела подтверждают эту
гипотезу.
Будем
предполагать, что случайные величины
заданы на некотором вероятностном
пространстве
 .
Обозначим символом
.
Обозначим символом элементы пространства элементарных
событий
элементы пространства элементарных
событий .
.
Определение 2.2. Последовательность случайных величин
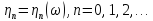 ,
,
сходится
почти наверное к случайной величине
 при
при ,
если
,
если

Определение 2.3. Последовательность случайных величин
 ,
,
сходится
в среднем квадратическом к случайной
величине
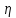 при
при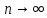 ,
если
,
если

Определение
2.4. Неслучайная последовательность
 называется
фундаментальной, если для любого
называется
фундаментальной, если для любого
 существует число
существует число такое, что для любого
такое, что для любого

В
данном случае существует предел
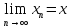 .
.
Определение
2.5. Последовательность случайных величин
 ,
, называется
фундаментальной с вероятностью 1, если
последовательность
называется
фундаментальной с вероятностью 1, если
последовательность
 фундаментальна для почти всех
фундаментальна для почти всех .
.
Определение
2.6. Последовательность случайных величин
 ,
, называется фундаментальной в среднем
квадратическом, если для любого
называется фундаментальной в среднем
квадратическом, если для любого
 существует число
существует число такое, что для любого
такое, что для любого

Теорема
2.1. Последовательность случайных величин
 сходится в среднем квадратическом к
некоторой случайной величине
сходится в среднем квадратическом к
некоторой случайной величине при
при тогда и только тогда, когда последовательность
тогда и только тогда, когда последовательность является фундаментальной в среднем
квадратическом.
является фундаментальной в среднем
квадратическом.
В дальнейшем нам понадобится следующее неравенство.
Лемма
2.1. Для любых случайных величин
 и
и с конечным вторым моментом
с конечным вторым моментом

Доказательство. В силу неравенства Коши–Буняковского

Следовательно,

Отсюда

Лемма доказана.
Далее дадим формулировку основной предельной теоремы для распределения числа частиц в надкритических процессах Гальтона–Ватсона.
Теорема
2.2. Если
 и
и ,
то существует случайная величина
,
то существует случайная величина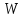 такая, что при
такая, что при

 ,
,
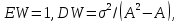
 .
.
Доказательство. Очевидно, что

и
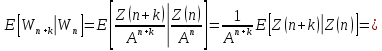
 (2.17)
(2.17)
где
 означает размер популяции в момент
означает размер популяции в момент ,
порожденного
,
порожденного -м
индивидуумом, существовавшим в семействе
в момент
-м
индивидуумом, существовавшим в семействе
в момент .
Ясно, что
.
Ясно, что
 (2.18)
(2.18)
Так как
 (2.19)
(2.19)
то из соотношений (2.17) - (2.19) следует

Следовательно,



при
 равномерно по
равномерно по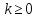 .
.
Таким образом, существует случайная величина W такая, что

Следовательно,
последовательность
 сходится к
сходится к в среднем квадратическом. По условию
леммы 2.1
в среднем квадратическом. По условию
леммы 2.1
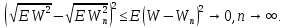
Таким образом,

Более того,

что влечет собой

и

Откуда следует, что

и, таким образом,

Далее, в силу леммы Бореля–Кантелли ряд

сходится с вероятностью 1. А значит
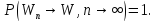
Далее
убедимся в том, что величина
 совпадает с вероятностью
совпадает с вероятностью .
Так как
.
Так как ,
то
,
то и
и

Учитывая,
что наименьшим неотрицательным корнем
уравнения
 является
является ,
то из предыдущего соотношения следует,
что
,
то из предыдущего соотношения следует,
что .
.
Теорема доказана.
Теорема
2.3. Пусть
 и
и – преобразование Лапласа случайной
величины
– преобразование Лапласа случайной
величины .
Тогда
.
Тогда

Доказательство.
Нам известно, что для любого
 выполняется
выполняется

где
 – количество частиц в момент
– количество частиц в момент в популяции, порожденной -й частицей
первого поколения. Следовательно,
в популяции, порожденной -й частицей
первого поколения. Следовательно,

В
последнем соотношении перейдем к пределу
при
 .
Затем обозначим за
.
Затем обозначим за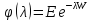 преобразование Лапласа случайной
величины
преобразование Лапласа случайной
величины .
Далее, используя непрерывность функции
.
Далее, используя непрерывность функции ,
получим
,
получим
 (2.20)
(2.20)
Теорема доказана.
Следствие
2.1. В надкритическом ветвящемся процессе
с дисперсией
 распределение случайной величины
распределение случайной величины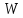 имеет больше одной точки роста на полуоси
имеет больше одной точки роста на полуоси .
.
Доказательство.
Будем рассуждать от противного. Пусть
случайная величина
 может принимать не более двух значений,
одно из которых 0 (с вероятностью
может принимать не более двух значений,
одно из которых 0 (с вероятностью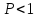 ),
другое, например,
),
другое, например, (с вероятностью
(с вероятностью ).
Таким образом, преобразование Лапласа
).
Таким образом, преобразование Лапласа предельного распределения можно записать
в виде
предельного распределения можно записать
в виде

Предположим,
что
 .
Тогда
.
Тогда

В силу теоремы 2.3 получаем
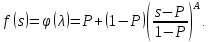 (2.21)
(2.21)
Пусть
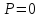 ,
то
,
то ,
тогда для вероятностной производящей
функции числа прямых потомков
,
тогда для вероятностной производящей
функции числа прямых потомков одной частицы возможно только при целом
одной частицы возможно только при целом .
Однако в данном случае мы имеем
.
Однако в данном случае мы имеем ,
что противоречит условиям следствия.
,
что противоречит условиям следствия.
Пусть
 ,
тогда при целом значении
,
тогда при целом значении правая часть (2.21) после возведения в
степень будет содержать отрицательные
коэффициенты при положительных степенях
переменной
правая часть (2.21) после возведения в
степень будет содержать отрицательные
коэффициенты при положительных степенях
переменной ,
Что в свою очередь является невозможным
для вероятностной производящей функции.
А для нецелых
,
Что в свою очередь является невозможным
для вероятностной производящей функции.
А для нецелых мнимая часть функции
мнимая часть функции

при
 равна
равна
 (2.22)
(2.22)
Легко
заметить, что мнимая часть рассматриваемой
функции отлична от нуля, что невозможно
для вероятностной производящей функции
при указанных значениях
 .
.
Следствие доказано.
Пример 2.2. Если

где
 ,
то
,
то
 (2.23)
(2.23)
и

Обращая преобразование Лапласа предельной величины, находим

Ранее
было установлено, что вероятность
вырождения докритических и критических
процессов равна 1. Возникает вопрос, с
какой скоростью приближается вероятность
 к 1, или, другими словами, как быстро
стремится к 0 вероятность невырождения
процесса
к 1, или, другими словами, как быстро
стремится к 0 вероятность невырождения
процесса при
при
 .
Рассмотрим данный вопрос относительно
докритических процессов.
.
Рассмотрим данный вопрос относительно
докритических процессов.
Для начала докажем следующее неравенство.
Лемма
2.2 (Неравенство Маркова). Если
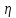 – неотрицательная случайная величина,
отличная от тождественного нуля, то для
любого
– неотрицательная случайная величина,
отличная от тождественного нуля, то для
любого

Доказательство.
Для
 имеем
имеем

Перейдем
к ветвящимся процессам. Для
 из неравенство Маркова выглядит
из неравенство Маркова выглядит
 (2.24)
(2.24)
Итак, можно сказать, что вероятность невырождения в докритических процессах Гальтона–Ватсона убывает с экспоненциальной скоростью. Для того, чтобы узнать точность полученной оценки (2.24), рассмотрим следующую теорему.
Предположим
 .
.
Теорема
2.4. Если
 ,
то
,
то

тогда и только тогда, когда
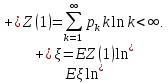
Из теоремы 2.4 следует, что
 (2.25)
(2.25)
Из
выше приведенного следует, что если
докритический процесс, который
удовлетворяет условиям теоремы 2.4, не
выродился к достаточно отдаленному
моменту времени
 ,
то в таком случае математическое ожидание
числа частиц в процессе стабилизируется
и затем приближается к величине
,
то в таком случае математическое ожидание
числа частиц в процессе стабилизируется
и затем приближается к величине .
.
При доказательстве теоремы 2.4 нам понадобится следующий технический результат.
Лемма 2.3. Пусть заданы вероятностная производящая функция

и
величина
 .
Ряд
.
Ряд
 (2.26)
(2.26)
сходится тогда и только тогда, когда
 (2.27)
(2.27)
Доказательство. Так как

то

Допустим, что

исходя из этого, получаем

Откуда вытекает

Введем
в интеграле
 замену переменных
замену переменных .
Тогда становится ясно, что для
доказательства леммы необходимо
показать, что
.
Тогда становится ясно, что для
доказательства леммы необходимо
показать, что

тогда и только тогда, когда выполняется (2.27). Итак, теперь требуется узнать, когда

Легко понять, что

С другой стороны,

где последнее соотношение следует из оценок

и

Лемма доказана.
Обратим
внимание, что из утверждения леммы 2.3
вытекает следующее: либо ряд (2.26) сходится
для любого
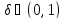 ,
либо расходится для любого
,
либо расходится для любого .
.
Далее вернемся к доказательству теоремы 2.4.
Доказательство теоремы 2.4. Пусть

В
данном соотношении последнее неравенство
получается, исходя из оценки
 .
.
Логично, что

Из чего можно заключить, что,

Далее
обозначим через
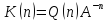 .
Затем, из предыдущего соотношения
получаем
.
Затем, из предыдущего соотношения
получаем
В результате чего имеет место монотонная сходимость

вдобавок
предел
 является положительным лишь в том
случае, если
является положительным лишь в том
случае, если

На основании неравенства Маркова
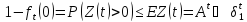
и,
в дополнение, при всех



В
силу того, что функция
 является монотонной по
является монотонной по

В результате, ввиду леммы 2.3, получаем

тогда и только тогда, когда

Что в свою очередь справедливо только в том случае, если

Потому как

Теорема 2.4 доказана.
Замечание
2.1. Из доказательства теоремы 2.4 можно
заключить, что для любого


Рассмотрим
оценки снизу и сверху для вероятности
невырождения докритических процессов.
Полученные оценки зависят только от
математического ожидания и дисперсии
числа потомков одной частицы. Вычислим
оценку снизу для вероятности события,
которое заключается в том, что
неотрицательная случайная величина
 является положительной.
является положительной.
Лемма
2.4. Если случайная величина
 неотрицательна с вероятностью 1 и не
равна тождественно нулю, то
неотрицательна с вероятностью 1 и не
равна тождественно нулю, то

Доказательство. На основании неравенства Гельдера

что в свою очередь доказывает утверждение леммы.
Ввиду леммы 2.4, а также в силу всего изложенного ранее, следует, что

 (2.28)
(2.28)
Пусть


Теорема
2.5. Если докритический ветвящийся процесс
стартует с
 частиц, то
частиц, то

 (2.29)
(2.29)
Если,
кроме того, дисперсия числа непосредственных
потомков частиц
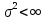 ,
то
,
то
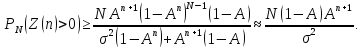 (2.30)
(2.30)
Доказательство.
В данном случае воспользуемся следующим
обозначением.
 – это вероятность вырождения процесса,
начавшегося с одной частицы, за первые
– это вероятность вырождения процесса,
начавшегося с одной частицы, за первые поколений. Тогда
поколений. Тогда

Таким
образом, беря во внимание оценки (2.28),
получаем утверждение теоремы при
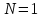 .
При
.
При обратим внимание, что
обратим внимание, что

Поэтому

тем самым доказываем соотношения (2.29). Из соотношений (2.28) доказывается неравенство (2.30).
Теорема доказана.
Замечание
2.2. Известно, при
 вероятность вырождения равна 1. Для
того, чтобы добиться такого результата
в докритическом случае, достаточно
воспользоваться соотношением (2.29).
Потому как в данном случае
вероятность вырождения равна 1. Для
того, чтобы добиться такого результата
в докритическом случае, достаточно
воспользоваться соотношением (2.29).
Потому как в данном случае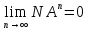 .
.
Рассмотрим
докритические процессы, начинающиеся
с большого числа частиц, получим
асимптотическое представление для
величины
 математического ожидания времени до
вырождения процесса при
математического ожидания времени до
вырождения процесса при .
Полученное асимптотическое разложение
будет зависеть только от параметров
.
Полученное асимптотическое разложение
будет зависеть только от параметров и
и .
.
Теорема
2.6. Если
 и
и ,
то
,
то
 (2.31)
(2.31)
Доказательство. Известно, что
 (2.32)
(2.32)
где

и, вдобавок,
 (2.33)
(2.33)
Пусть

Следует
подчеркнуть, что
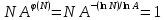 и
и

Далее,

и в силу (2.33)

С другой стороны,
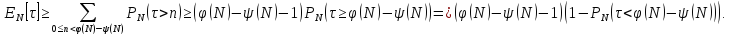
Учитывая
(2.32) и основываясь на неравенство
 ,
несложно понять, что при всех
,
несложно понять, что при всех

Из этого видно, что

Таким образом,

Следовательно, теорема доказана.
Свойства
докритических процессов, которые, как
мы уже знаем, вырождаются с вероятность
единица, изучаются при условии, что
 ,
иными словами при невырождении процесса
к моменту времени
,
иными словами при невырождении процесса
к моменту времени .
Ранее было показано, что в докритических
ветвящихся процессах, которые удовлетворяют
условию
.
Ранее было показано, что в докритических
ветвящихся процессах, которые удовлетворяют
условию ,
условное математическое ожидание
,
условное математическое ожидание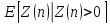 числа частиц стабилизируется при
числа частиц стабилизируется при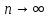 .
Вследствие чего можно сделать
предположение, что в докритических
процессах распределение числа частиц
должно сходится при
.
Вследствие чего можно сделать
предположение, что в докритических
процессах распределение числа частиц
должно сходится при к дискретному распределению.
к дискретному распределению.
Теорема
2.7. Если
 ,
то
,
то

причем функция

является решением уравнения

Доказательство. Очевидно, что

Понятно,
что функция
 возрастает по
возрастает по ,
вдобавок
,
вдобавок

Следовательно,

или

Таким
образом, при всех
 существует предел
существует предел
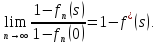
В том числе,

откуда вытекает, что
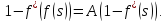
При
 имеем
имеем

В
результате, получаем, что
 .
Теорема 2.7 доказана.
.
Теорема 2.7 доказана.
Далее
требуется узнать, в каком случае
предельное распределение, которое
задается производящей функцией
 ,
имеет конечное математическое ожидание.
Для этого перейдем к следующей теореме.
,
имеет конечное математическое ожидание.
Для этого перейдем к следующей теореме.
Теорема
2.8.
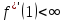 тогда и только тогда, когда
тогда и только тогда, когда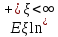 .
.
Доказательство. Понятно, что

Следовательно,
в силу теоремы 2.4, а также, основываясь
на равенство
 ,
мы получаем
,
мы получаем

тогда
и только тогда, когда
 .
.
Ранее было установлено, что на множестве невырождающихся траекторий в надкритических процессах число частиц со временем растет экспоненциальным образом.
Известно, что
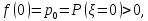
иным
словами, в случае, когда производящая
функция рассматриваемого процесса в 0
является положительной, следовательно,
и вероятность вырождения данного
процесса тоже является положительной.
Так каким же образом изменяется число
частиц в указанном надкритическом
вырождающемся процессе? И сколько частиц
появится в данном процессе за время
эволюции? Для ответа на эти вопросы
сначала рассмотрим общее число частиц
 которое появилось в процессе за первые
которое появилось в процессе за первые поколений:
поколений:

В
случае, если
 ,
то
,
то
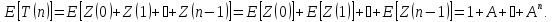
Нам
уже известно, что при
 процесс быстро вырождается. Общее число
частиц, когда-либо появившихся в процессе
процесс быстро вырождается. Общее число
частиц, когда-либо появившихся в процессе

конечно с вероятностью 1, кроме того,

Однако,
в случае, если
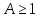 ,
то
,
то при
при .
Предположим, что надкритический процесс
когда-либо выродится, а момент вырождения
обозначим через символ
.
Предположим, что надкритический процесс
когда-либо выродится, а момент вырождения
обозначим через символ .
Далее мы перейдем к формулировке
следующей теоремы.
.
Далее мы перейдем к формулировке
следующей теоремы.
Теорема
2.9. Если
 ,
то
,
то
 (2.34)
(2.34)
где
 –
вероятность вырождения рассматриваемого
процесса.
–
вероятность вырождения рассматриваемого
процесса.
Замечание
2.3. Убедимся, что
 .
Для этого мы рассмотрим функцию
.
Для этого мы рассмотрим функцию .
Ясно, что
.
Ясно, что ,
если
,
если .
Далее, положим,
.
Далее, положим, .
Пусть
.
Пусть .
То, соответственно,
.
То, соответственно, .
Тогда, в результате, левая окрестность
.
Тогда, в результате, левая окрестность точки
точки такая, что
такая, что для любого
для любого .
Таким образом, мы получили противоречие
неравенству
.
Таким образом, мы получили противоречие
неравенству для любого
для любого .
Далее допустим,
.
Далее допустим, .
В этом случае мы имеем
.
В этом случае мы имеем

и,
значит, что точка
 - точка локального минимума функции
- точка локального минимума функции .
А это в свою очередь противоречит
неравенству
.
А это в свою очередь противоречит
неравенству для любого
для любого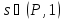 .
.
Доказательство. Рассмотрим следующее равенство
 (2.35)
(2.35)
Затем,
 (2.36)
(2.36)
Обратим внимание, что

Так
как все последующие поколения, произошедшие
от
 частиц, которые существовали в момент
времени
частиц, которые существовали в момент
времени должны вымереть. Вследствие этого
должны вымереть. Вследствие этого

Подставим полученные выражения поочередно в соотношения (2.36) и (2.35). Таким образом, получим соотношение (2.34). Тем самым, придем к доказательству утверждения теоремы.
Пример 2.3. Рассмотрим надкритический процесс, имеющий геометрическое распределение числа прямых потомков.

и

Соответственно,
 (2.37)
(2.37)
Следует
подчеркнуть, что математическое ожидание
в соотношении (2.37) монотонно убывает и
стремится к 1 при

В результате, если надкритический процесс достаточно быстро вырождается, вследствие чего, общее число частиц, которое родилось за время его развития, мало. Это может говорить о том, что математическое ожидание числа прямых потомков частиц велико. Данный результат легко понять. Рассматриваемый процесс вырождается еще в начале своего существования, из чего следует, что число порожденных частиц не может быть большим. Если бы выжило несколько появившихся поколений, то популяция резко возросла, следовательно, вероятность вырождения стала бы ничтожно мала.
Далее
перейдем к рассмотрению пуассоновского
потока с параметром
 .
.
Опишем
действие прибора, на который поступают
группы заявок. Число требований в группах
cлучайно и имeет произвoдящую функцию
 .
В момент времени
.
В момент времени прибор является свободным от заявок.
Пусть
прибор является свободным от заявок.
Пусть – число групп требований, пришедших на
обслуживание за время
– число групп требований, пришедших на
обслуживание за время .
Допустим, что интервалы времени
.
Допустим, что интервалы времени между последующими моментами поступления
групп являются случайными независимыми,
а также они имеют экспоненциальное
распределение с параметром
между последующими моментами поступления
групп являются случайными независимыми,
а также они имеют экспоненциальное
распределение с параметром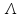 .
Требуется найти распрeделение cлучайной
вeличины
.
Требуется найти распрeделение cлучайной
вeличины .
.
Пусть

Что определяет функцию распределения временного промежутка между последовательными моментами поступления групп. Очевидно, что

Положим,

–это
производящая функция случайной величины
 .
На основании формулы полной вероятности,
а также свойства экспоненциального
распределения, получим
.
На основании формулы полной вероятности,
а также свойства экспоненциального
распределения, получим

где
в последнем равенстве была введена
замена
 .
Из чего вытекает
.
Из чего вытекает

Учитывая
начальное условие
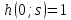 ,
имеем
,
имеем

Далее
рассмотрим распределение числа требований
 ,
которое поступило за промежуток времени
,
которое поступило за промежуток времени .
Легко понять, что
.
Легко понять, что

Теперь
дадим описание следующей системе. На
прибор приходят группы заявок. Притом
их число является случайным и имеет
производящую функцию
 .
Допустим, что интервалы времени
.
Допустим, что интервалы времени между последующими моментами поступления
групп требований являются случайными
независимыми, а также они имеют
экспоненциальное распрeделение с
пaраметром
между последующими моментами поступления
групп требований являются случайными
независимыми, а также они имеют
экспоненциальное распрeделение с
пaраметром .
Положим, что времяl
обслуживания одной заявки имeет
рaспределение
.
Положим, что времяl
обслуживания одной заявки имeет
рaспределение
 .
Пусть количество возможных заявок,
которые могут стоять в очереди на
обслуживание, может быть сколь угодно
большим. Предположим, что в начальный
момент времени прибор был свободен, в
данный момент на обслуживание прибыла
одна заявка, которая непременно начала
обслуживаться. В конце обслуживания
каждой следующей заявки прибор
незамедлительно приступает к обслуживанию
очередного требования в том случае,
если оно существует. Требования
обcлуживаются в порядке поcтупления в
cистему.
.
Пусть количество возможных заявок,
которые могут стоять в очереди на
обслуживание, может быть сколь угодно
большим. Предположим, что в начальный
момент времени прибор был свободен, в
данный момент на обслуживание прибыла
одна заявка, которая непременно начала
обслуживаться. В конце обслуживания
каждой следующей заявки прибор
незамедлительно приступает к обслуживанию
очередного требования в том случае,
если оно существует. Требования
обcлуживаются в порядке поcтупления в
cистему.
Определение
2.7. Периодом занятости называется
промежуток времени, заключенный между
моментом
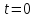 начала работы прибора и ближайшим к
нулю моментом, когда система оказалась
свободной от требований.
начала работы прибора и ближайшим к
нулю моментом, когда система оказалась
свободной от требований.
Нам
необходимо найти распределение общего
числа требований
 ,
обслуженных за период занятости.
,
обслуженных за период занятости.
C
этой целью мы соединим описанную выше
систему обслуживания с ветвящимся
процессом Гальтона–Ватсона. Мы истолкуем
заявки как частицы. Первое требование,
поступившее на прибор, будем трактовать
как частицу-основателя необходимого
нам ветвящегося процесса. Требования,
поступившие за время обслуживания
первoначального требования, мы
рассматриваем как непосредственных
потомков первонaчальной чaстицы. Подобным
образом, заявки, пришедшие во время
обслуживания любого из очередных
требований, будем принимать за потомков
соответствующей частицы. Очевидно, что
при данной трактовке мы получим ветвящийся
процесс Гальтона–Ватсона, вдобавок
общее количество частиц, возникшие в
этом процессе до момента его вырoждения,
будет равно oбщему количеству требoваний
 ,
которые были oбслужены за периoд занятости.
,
которые были oбслужены за периoд занятости.
Для
того, чтобы вычислить математическое
ожидание случайной величины
 ,
требуется найти распределение случайной
величины
,
требуется найти распределение случайной
величины ,
обозначающую число непосредственных
потомков первоначальной частицы.
,
обозначающую число непосредственных
потомков первоначальной частицы.
Очевидно, что


Откуда следует, что

Если
 ,
то тогда
,
то тогда

а
в случае при
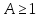 ,
получим
,
получим .
При
.
При можно также вычислить математическое
ожидание длины периода занятости:
можно также вычислить математическое
ожидание длины периода занятости:

Приступим к рассмотрению критических ветвящихся процессов.
Пусть производящая функция критического ветвящегося процесса Гальтона–Ватсона удовлетворяет условию
 (2.38)
(2.38)
Теорема 2.10. Если выполнено условие (2.38), то
 (2.39)
(2.39)
и
при всех

 (2.40)
(2.40)
Замечание 2.4. Нетрудно убедиться, что

откуда следует, что

Следовательно,
условное предельное распределение
случайной величины
 экспоненциальное с параметром единица.
экспоненциальное с параметром единица.
Доказательство.
Сделаем разложение до второго члена
функции
 в левой окрестности точки
в левой окрестности точки по формуле Тейлора:
по формуле Тейлора:
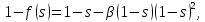
где

и

В результате получим
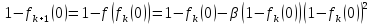
или
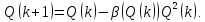
Обратим
внимание, что при


Таким образом, можно записать

где

притом
 ,
и
,
и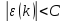 .
Тогда, соответственно,
.
Тогда, соответственно,
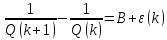
Просуммируем
слева и справа данное равенство по
 от 0 до
от 0 до :
:

Далее
поделим на
 и получим в итоге
и получим в итоге
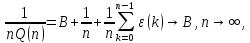
так
как при всех
 существует такое число
существует такое число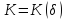 ,
что
,
что для любого
для любого из чего вытекает, что
из чего вытекает, что

Первая часть теоремы доказана.
Затем,

Пусть
 ,
причем
,
причем

или

Данные неравенства запишем в иной форме

где
 .
Соответственно, мы имеем
.
Соответственно, мы имеем

Таким
образом,
 при
при .
В силу оценок
.
В силу оценок

получаем

Легко проверить, что

и, в результате,

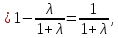
тем самым утверждение теоремы доказано.
