2 Ветвящиеся процессы. Основные понятия

2.1 Ветвящиеся процессы и их классификация

Рассмотрим процессы Гальтона-Ватсона. Пусть дано распределение вероятностей на множестве

И пусть для целых чисел и

- значение k-кратной свертки распределения с собой в точкеj.

Ясно, что если а, - последовательность независимых случайных величин таких, чтопри всех, то

Определение 2.1. Цепь Маркова с начальным распределением вероятностей на множествеи переходными вероятностями

Представим определение ветвящихся процессов Гальтона-Ватсона на языке эволюции популяции частиц. Пусть в данной популяции изначально имеется одна частица: , которая имеет единичную продолжительность жизни. В соответствии с вероятностным распределением

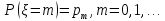
эта частица в конце жизни производит случайное число потомков .

Каждая новорожденная частица имеет единичную продолжительность жизни, в конце которой производит случайное число потомков в соответствии с распределением . Следовательно, при

Где обозначает количество потомковi-той частицы n-го поколения (), причемпри всехии независимы.

Дадим описание вероятностного пространства.

Процeсс Гальтона–Ватсона будет задан на вероятностном пространстве , детальное описание которого приведено далее. Для начала мы припишeм частицам рассматриваемого процесса слeдующие обозначeния. Пeрвоначальная частица будет обозначаться символом, а ееi-й потомок – символом . Следовательно, частицыn-го поколeния будут нумeроваться наборами

Далее обозначим через количество потомков частицы. В данной символике реализация эволюции популяции будет иметь вид

Таким образом, пространством элементарных событий является объединение всех возможных реализаций эволюций популяций, а σ-алгебрапорождается цилиндрическими подмножествами пространства.

Рассмотрим поколения популяции. Для каждого введем последовательность, гдесимволизирует множество частиц, образующихn-е поколение. Элементы данной последовательности задаются следующим образом.

а состоит из всех последовательностейтаких, что

и . Если, то, естественно,для всех.

С каждой реализацией эволюции популяции можно ассоциировать плоское корневое ориентированное дерево с вершинами, обозначенными метками

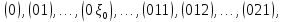
и ребрами, направленными от корня. Отметим корень дерева символом 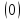, кoторый сoответствует первоначальной частицe процесса. Вeршины, соeдиненные с корнeм, отмечены символами, которые соответствуeт частицам первого поколения и т.д.

Вероятностная мера задается на цилиндрических подмножествах, которые являются элементами σ-алгебры. Данная величина описывается при помощи соотношений

и

естественным образом продолжается на все элементы σ-алгебры .

Приведенная выше конструкция описывает вероятностное пространство , на котором задан ветвящийся процесс Гальтона–Ватсона.

Введем понятие производящих функций. Рассмотрим ветвящийся процесс Гальтона–Ватсона . Пусть

(2.1)

– вероятностная производящая функция, которая задает распределение случайной величины числа прямых потомков частиц рассматриваемого процесса. Очевидно, что

и

Пример 2.1. Предположим, что число прямых потомков частиц в ветвящемся процессе имеет геометрическое распределение, задаваемое для , производящей функцией

где .

Очевидно, что .

Последовательность функций

называется итерациями производящей функции .

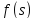Довольно часто в биологических приложениях используется производящая функция следующего вида

.

Важно отметить, что выгодность итераций производящих функций в теории ветвящихся процессов проявляется в том, что если , то

Ветвящиеся процессы Гальтона–Ватсона можно разделить на три класса: докритический, критический и надкритический. Классификация определяется значением параметра

Процесс Гальтона–Ватсона является докритическим, если , критическим, если, и надкритическим, если.

Математическое ожидание и дисперсия числа индивидуумов n-го поколения вычисляются с помощью следующих формул

и

(2.2)

что, в свою очередь, приводит к равенству

Таким образом, если , то

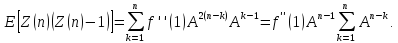
Упростив полученное выражение, мы получим

пр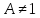и , и

в критическом случае. Следовательно, при

(2.3)

(2.4)

Отсюда, принимая во внимание равенство

и предположение , получаем, что

(2.5)

Коэффициентом вариации 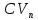популяции в моментn называется величина

Для надкритических процессов коэффициент вариации при больших 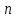удовлетворяет соотношению

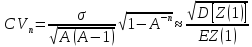
и быстро стабилизируется. Для критических процессов

а для докритических процессов

Таким образом, можно сделать вывод, что критические и докритические процессы Гальтона–Ватсона являются нестабильными.

Рассмотрим производящую функцию

Очевидно, что . Нетрудно понять, что

и

Таким образом, для итераций , справедлива цепочка равенств

т.е.

Таким образом, если , то

(2.6)

Если же , то

Используя полученные равенства, можно без затруднений вычислить вероятность выживания процесса в течение поколений: если, то

Если же , то

При

Рассмотрим элементарные свойства производящих функций.

Положим, что

– вероятностная производящая функция. Для того, чтобы в будущем исключить тривиальные случаи, допустим, что . Тогда при данном условии

1. строго выпуклая функция на ;

2. ;

3. eсли , то 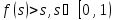, так какипри;

4. если 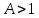, то уравнениеимеет единственный корень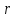на полуинтервале, причемпри и при. Справедливость этих неравенств вытекает из оценок

и

.

Далее ведем понятие вероятности вырождения.

Ранее мы получили, что

Следовательно, вероятность вырождения процесса . Так как справедлива импликация

{

то

Из чего следует, что последовательность

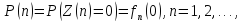
монотонно возрастая, стремится к вероятности вырождения процесса :

Пусть

Так как , то

Вследствие того, что функция является непрерывной, можно записать. Следовательно,

Таким образом, докритические и критические процессы вырождаются с вероятностью 1, в то время как вероятность вырождения надкритического процесса 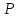меньше 1 и является наименьшим неотрицательным корнем уравнения.

Рассмотрим ветвящийся процесс с геометрическим законом распределения числа потомков:

(2.7)

Вероятность вырождения такого процесса равна

Заметим, что

(2.8)

где - это независимые одинаково распределенные случайные величины, , причем. Кроме того, в случае

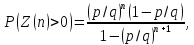(2.9)

а при

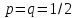
(2.10)

Рассмотрим простое случайное блуждание

где - множество всех целых чисел, а

Зафиксируем число 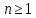. Допустим, что блужданиестартует из точки, а останавливается в том случае, если оно впервые окажется либо в точке -1, либо точкеn. Далее нам необходимо вычислить вероятность того, что блуждание закончится точке n. Для этого требуется ввести следующие обозначения:

- блуждание стартует из точки и останавливается в точкевнутри временного интервала;- блуждание стартует из точкии останавливается в точкенаN-м шаге.

Положим, что

, .

Ясно, что при

в то время как

Заметим теперь, что

(2.11)

Поэтому при каждом существует предел

Учитывая это и устремляя к бесконечности в обеих частях равенства (2.11), получаем уравнения

с граничными условиями

Для того, чтобы получить решение данной системы уравнений, необходимо составить характеристическое уравнение

Откуда получаем

Решения последнего уравнения имеют вид

Таким образом, при общее решение рассматриваемой системы имеет вид

Учитывая граничные условия, находим

и

Следовательно,

что дает

Таким образом,

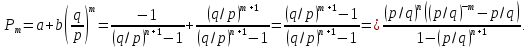
В частности,

(2.12)

Заметим, что

(2.13)

При общее решение имеет вид

.

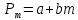С учетом граничных условий, получаем

Откуда

Следовательно,

В частности,

(2.14)

Величина определяет вероятность того, что случайное блуждание, стартующее из 0 никогда не попадет в точку -1.Eсли 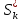– простое случайное блуждание, которое стартовало из 0 и остановилось в момент, когда оно в первый раз приняло значение -1:, то

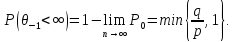
Рассмотрим связь между простым случайным блужданием и ветвящимся процессом. Для этого введем обозначение

(2.15)

Предположим, что 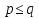. Несложно видеть, что тогда, а случайная величина

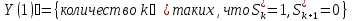
имеет следующее распределение:

Итак, для любого ,

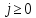где

(2.16)

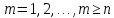Пусть далее для некоторого , и пусть

.

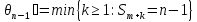Вследствие того, что простое случайное блуждание однороднo, число шагов с уровня на уровеньв промежуткеслучайно, а также оно имеет геометрическое распределение с параметром. Следовательно, еслизадается соотношением (2.15), иными словами равно числу переходов исходного случайного блуждания с уровня n на уровень, то

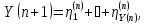
где случайные величины , независимы и одинаково распределены, причем.

В результате мы получаем ветвящийся процесс, аналогичный (2.8).

Из изложенного выше очевидно, что при событие, заключающееся в том, что блуждание окажется в точкедо того, как оно окажется в точке −1, соответствует событиюдля ветвящегося процесса с чисто геометрической производящей функцией числа потомков. Таким образом поясняется сходство формул (2.9) и (2.10) с формулами (2.12) и (2.14), соответственно.

Отметим, что ветвящийся процесс с производящей функцией (2.7) вырождается с вероятностью 1 в том случае, если . Далее если– момент вырождения процесса, то общее число частиц, родившихся в процессе за время эволюции, равно

Нетрудно проверить, что