diplom25 / suslov_ibragimov_ekonometrika

Обычно S0 = (−∞, s ] и S1 = (s , +∞),где s Ñкритическая граница.Такойкритерийназываетсяодносторонним.Приэтомкритерийсостоитвследующем:

если s < s ,то H0 принимается, если s > s ,то H0 отвергается.

S0 и S1 выбираются так,чтобы в случае,когда H0 верна,вероятность того, что s S1 ,былабыравнанекоторойзаданной малойвероятности α.Какправило, на практике используют вероятность α = 0.05 (хотя это не имеет под собой какихлибо теоретических оснований).

Ошибкой первого рода называется ошибка,состоящая в том,что отвергается верная нулевая гипотеза.Вероятность ошибки первого рода равна α.Вероятность ошибки первого рода называется уровнем значимости или размером.Вероятность 1 − α называют уровнем доверия.

Ошибкой второго рода называется ошибка,состоящая в том,что принимается неверная нулевая гипотеза.Вероятность ошибки второго рода обозначают β.

Мощностью критерия называют величину 1 −β.Мощность характеризует,насколько хорошо работает критерий.Мощность должна быть как можно большей при данном α.Требуется,по крайней мере,чтобы α < 1 − β.Критерий,не удовлетворяющий этому условию,называют смещенным.

Альтернативныйспособпроверкигипотезиспользуетвероятностьошибкипервого рода,еслипринять s равной s,т.е.вероятность того,что s > s .Эту вероятность называют уровнем значимости илиP-значением.Обозначим ее pv.При заданной вероятности α критерий состоит в следующем:

если pv >α ,то H0 принимается, если pv <α ,то H0 отвергается.

Еще один способ проверки гипотез основан на доверительных областях для параметра θ.Пусть D Ñдоверительная область для параметра θ,такая что θ D с некоторой веротностью 1 − α,и пусть проверяется гипотеза H0: θ = θ0 против альтернативной гипотезы H1: θ =! θ0.Критерий состоит в следующем:

если θ0 D,то H0 принимается, если θ0 / D,то H0 отвергается.

Отметим,что в этом случае θ0 не случайная величина;случайной является доверительная область D.

714 ПриложениеA.Вспомогательные сведения из высшей математики

A.4.Линейные конечно-разностные уравнения

Конечно-разностное уравнение p-го порядка имеет вид:

α0yt + α1yt−1 + ááá + αpyt−p = ut ,

где ut Ñизвестная последовательность, α0, α1, . . . ,α p Ñизвестные коэффициенты,апоследовательность yt следуетнайти.Этоуравнениетакжеможнозаписать через лаговый многочлен:

( )

α (L) yt = α0 + α1L + α2L2 + ááá + αpLp yt = ut ,

где L Ñлаговый оператор( Lyt = yt−1).

Если даны p последовательных значений последовательности yt ,например, y1, . . . , yp ,то другие значения можно н айти по рекуррентной формуле.При t > p получаем

Конечно-разностное уравнение называется однородным,если ut = 0.Общее решение конечно-разностного уравнения имеет вид:

yt = yt0 + y÷t ,

где yt0 Ñобщее решение соответствующего однородного уравнения, а y÷t = α−1 (L) ut Ñчастное решение неоднородного уравнения.

A.4.1.Решение однородного ко нечно-разностного уравнения

Если λj , j = 1, . . . , p Ñкорни характеристического уравнения

α (λ) = α0 + α1λ + α2λ2 + ááá + αp λp = 0,

Если все корни λj , j = 1, . . . , p различные,то общее решение однородного конечно-разностного уравнения имеет вид:

комплексно-сопряженными,можно заменить на

C1λ−1 t + C2λ−2 t = C1(Reiϕ)−t + C2(Re−iϕ)−t =

( )

= R−t C1e−iϕt + C2eiϕt = R−t (A cos(ϕt) + B sin(ϕt)) .

Если известны p значений последовательности yt0,например,

то коэффициенты Cj , Cj k , A, B находятся из решения системы p линейных урав-

A.5.Комплексные числа

Комплексным числом z называется пара (a, b),где aÑдействительная часть,

716 ПриложениеA.Вспомогательные сведения из высшей математики

¥Выполняется свойство zz = |z|2

¥Любоекомплексноечисло z = a+ib можнопредставитввиде z = |z|cos ϕ+

+ i|z|sin ϕ,где угол ϕ такойчто cos ϕ = |az| и sin ϕ = |zb|.Угол ϕ называют аргументом z.

¥Формула Эйлера: cos ϕ + i sin ϕ = eiϕ и cos ϕ − i sin ϕ = e−iϕ .

718 ПриложениеB.Статистические таблицы

Таблица А.1.Значения функции плотности стандартного нормального распределения

719

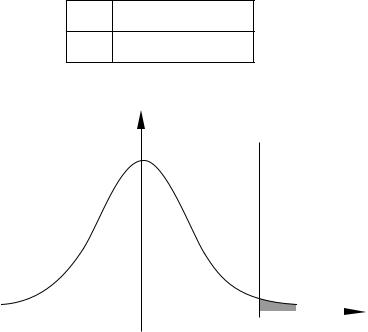
Распределение t-Cтьюдента

Pr(t > tk,1−θ ) = θ

Границы t-распределения с k степенями свободы tk,1−θ

θ = 0.025

k = 5 2.5%, t0.975 = 2.571

Распределение t6Стьюдента

Рис. B.2График плотности распределения t-Стьюдента для k = 5

721

Распределение хи-квадрат( χ2)

Pr(χ2 > χ2 − ) = θ.

k,1 θ

Границы χ2-распределения с k степенями свободы χ2k,1−θ .

θ = 0.05

k = 5 5% , χ0.95 = 11.07

Распределение хи-квадрат (χ2)

5%

Рис. B.3График плотности распределения χ2 для k =5