
IW_2_Math_Analysis
.pdf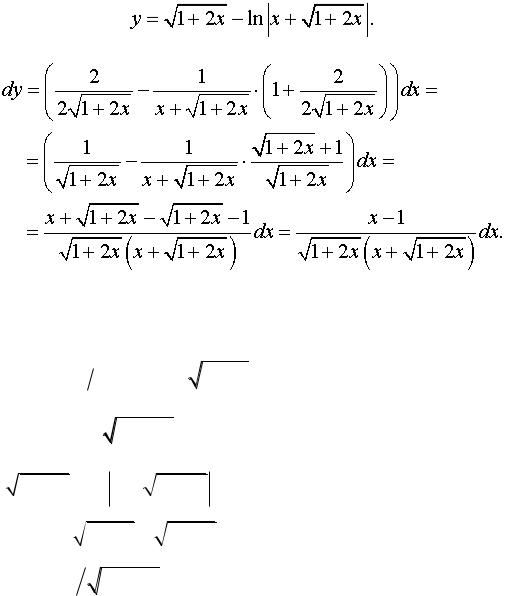
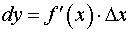 . (1)
. (1)
Дифференциал 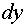 называют также дифференциалом первого порядка. Так как для
называют также дифференциалом первого порядка. Так как для
функции 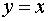 имеем
имеем 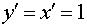 , то, согласно формуле (1), имеем
, то, согласно формуле (1), имеем 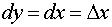 , т.е. дифференциал независимой переменной равен приращению этой
, т.е. дифференциал независимой переменной равен приращению этой
переменной: 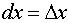 . Поэтому формулу (1) можно записать так:
. Поэтому формулу (1) можно записать так:
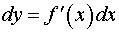 , (2)
, (2)
иными словами, дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной.
Задача 3. Найти дифференциал 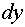 .
.
Задача 3. Найти дифференциал dy . |
|
||||||
|
|
|
|
|
|
||
3.1. y x arcsin 1 x ln |
x |
|
|
|
|
||
x2 1 |
, |
x 0. |
|||||
3.2. y tg 2arccos |
|
|
, |
|
|
|
|
|
|
|
|||||
1 2x2 |
x 0. |
|
|||||
3.3.y 
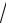 1 2x ln x
1 2x ln x 
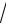 1 2x .
1 2x .
3.4.y x2 arctg 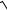
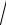 x2 1
x2 1 
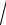 x2 1.
x2 1.
3.5. y arccos 1 |
|
, |
|
1 2x2 |
x 0. |
11
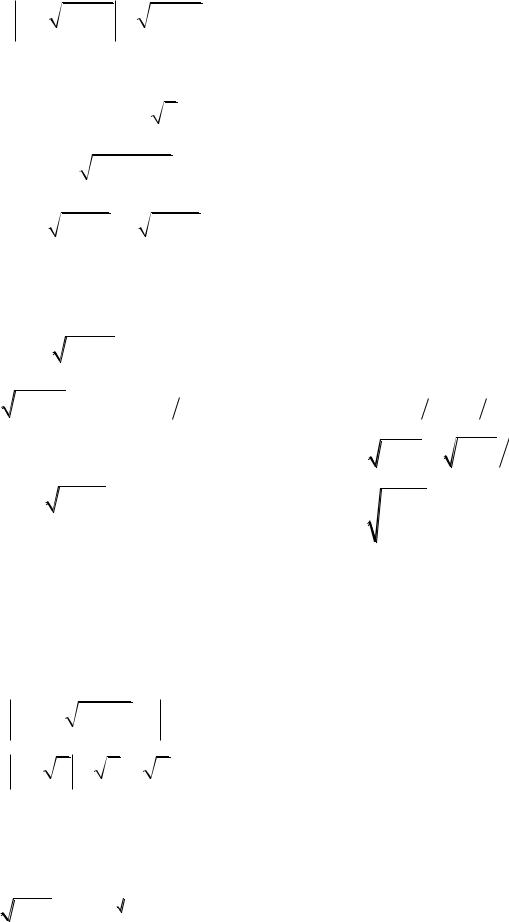
3.6.y x ln x 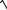
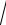 x2 3
x2 3 
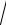 x2 3.
x2 3.
3.7.y arctg sh x sh x lnch x.
3.8.y arccos x2 1 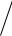 x2
x2 
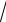 2 .
2 .
3.9.y ln cos2 x 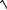
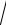 1 cos4 x .
1 cos4 x .
3.10.y ln x 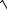
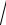 1 x2
1 x2 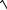
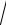 1 x2 arctg x.
1 x2 arctg x.
3.11. y |
ln |
x |
|
|
1 |
ln |
x2 |
||||
|
|
|
|
|
|
||||||
1 x2 |
2 |
1 x2 |
|||||||||
|
|
|
|||||||||
3.12. y ln ex |
|
|
arcsinex . |
||||||||
|
e2 x 1 |
||||||||||
|
|
|
|
|
|
|
|
a arcsin x |
2 . |
3.14. y lntg x |
|
2 x sin x. |
||||||||||||||||||
3.13. y x |
|
4 x2 |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.15. y 2x ln |
sin x 2cos x |
. |
|
3.16. y |
ctg x |
tg3 x 3. |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
3.17. y ln |
|
x |
|
x2 |
1 |
|
. |
|
|
3.18. y 3 |
x 2 |
. |
|
|
|
|
|
|
|
|||||||||||
|
|
|
2x |
|
|
|
|
|
|
x 2 |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
x2 |
|
1 |
|
|
|
|
|
3.20. y ln |
|
x2 1 |
|
|
1 |
|
|
|
||||||||||
3.19. y arctg |
|
. |
|
|
|
|
|
|
|
|
. |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
x |
x |
|
|
|
|
|
|
|
x2 1 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
3.21. y arctg |
tg |
|
|
1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
3.22. y ln 2x 2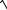
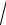 x2 x 1 .
x2 x 1 .
3.23. y ln cos 
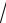 x
x 
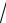 x tg
x tg 
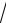 x.
x.
3.24. y ex cos 2x 2sin 2x .
3.25. y x sin ln x cosln x .
|
|
|
1 |
|
|
|
|
|
x 1 . |
||||
|
|
|||||
3.26. y |
x 1 |
|
e2 |
|||
|
||||||
|
|
|
2 |
|
|
|
12
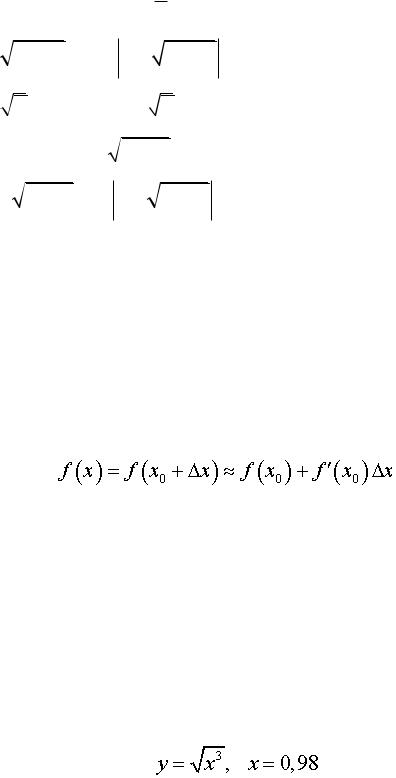
3.27.y cos x lntg x lntg 2x .
3.28.y 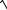
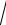 3 x2 x ln x
3 x2 x ln x 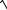
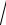 3 x2 .
3 x2 .
3.29.y 
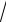 x 1 x arctg
x 1 x arctg 
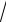 x.
x.
3.30.y x arctg x ln 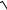
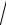 1 x2 .
1 x2 .
3.31.y x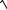
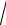 x2 1 ln x
x2 1 ln x 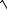
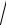 x2 1 .
x2 1 .
Дифференцирование. Задача 4
Приближенные вычисления с помощью дифференциала
Постановка задачи. Вычислить приближенно с помощью дифференциала значение функции 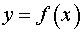 в точке
в точке 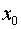 .
.
План решения. Если приращение 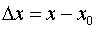 аргумента
аргумента 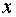 мало по абсолютной величине, то
мало по абсолютной величине, то
. (1)
1.Выбираем точку 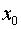 , ближайшую к
, ближайшую к 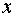 и такую, чтобы легко вычислялись значения
и такую, чтобы легко вычислялись значения 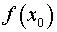 и
и  .
.
2.Вычисляем 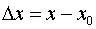 ,
, 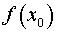 и
и 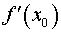 .
.
3.По формуле (1) вычисляем 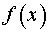 .
.
Задача 4. Вычислить приближенно с помощью дифференциала.
.
В нашем случае: 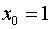 ,
, 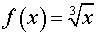 ,
, 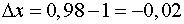 .
.
Вычисляем:
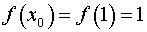 ; 13
; 13
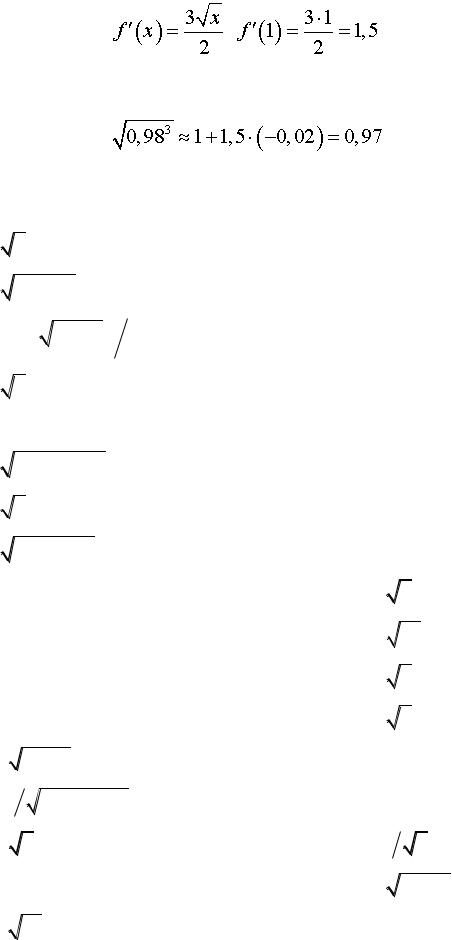
, |
. |
Имеем:
Задача 4. Вычислить приближенно с помощью дифференциала. |
|||||||||||||||
4.1. y 3 |
|
|
|
|
x 7,76. |
||||||||||
x, |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
4.2. y 3 |
x3 |
7x, |
|
x 1,012. |
|||||||||||
4.3. y x |
|
|
|
|
|
||||||||||
5 x2 |
2, x 0,98. |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||
4.4. y 3 |
x, |
x 27,54. |
|||||||||||||
4.5. y arcsin x, |
x 0,08. |
||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||
4.6. y 3 |
x2 |
2x 5, |
x 0,97. |
||||||||||||
|
|
|
|
|
|
|
|||||||||
4.7. y 3 |
x, |
x 26,46. |
|||||||||||||
|
|
|
|
|
|
||||||||||
4.8. y |
x2 |
x 3, |
x 1,97. |
||||||||||||
4.9. y x11, |
|
x 1,021. |
4.10. y 3 |
|
|
|
x 1,21. |
|||||||||
|
x, |
|||||||||||||||
4.11. y x21, |
|
|
x 0,998. |
4.12. y 3 |
|
|
|
x 1,03. |
||||||||
|
|
x2 , |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
4.13. y x6 , |
|
|
x 2,01. |
4.14. y 3 |
x, |
x 8,24. |
||||||||||
4.15. y x7 , |
|
|
x 1,996. |
4.16. y 3 |
|
|
x 7,64. |
|||||||||
|
|
x, |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
4.17. y |
4x 1, |
x 2,56. |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
4.18. y 1 |
|
|
2x2 x 1, |
x 1,016. |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
4.19. y 3 |
x, |
x 8,36. |
4.20. y 1 |
|
x , x 4,16. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
4.21. y x7 , |
|
|
x 2,002. |
4.22. y |
4x 3, |
x 1,78. |
||||||||||
|
|
|
|
|
|
|||||||||||
4.23. y |
x3 , |
x 0,98. |
4.24. y x5 , |
x 2,997. |
||||||||||||
|
|
|
|
|
|
|
|
|
14 |
|
|
|
|
|
|
|
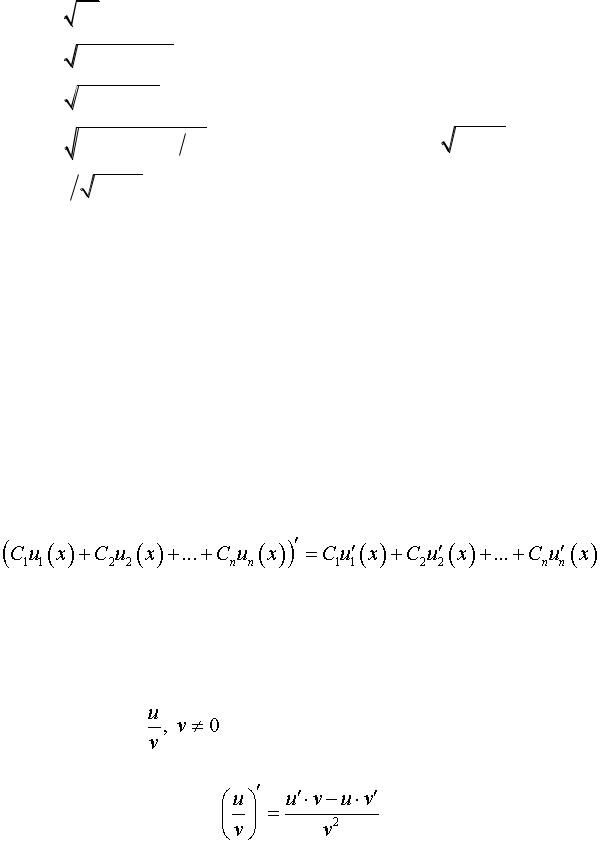
4.25. y 5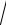 x2 , x 1,03. 4.26. y x4 , x 3,998.
x2 , x 1,03. 4.26. y x4 , x 3,998.
|
|
|
|
|
|
|
|
|
|
|
|
|
||
4.27. y |
1 x sin x, |
x 0,01. |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.28. y 3 |
|
3x cos x, |
|
|
x 0,01. |
|
|
|
|
|||||
|
|
|
|
|
|
, |
|
|
|
|
|
|||
4.29. y 4 |
|
2x sin x |
2 |
x 1,02. |
4.30. y |
x2 5, |
x 1,97. |
|||||||
|
|
|
|
|
|
|
|
|
|
|||||
4.31. y 1 |
|
|
2x 1, |
x 1,58. |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
Дифференцирование. Задача 5 |
|
|
|
|||
Вычисление производных
Постановка задачи. Найти производную функции 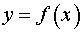 .
.
План решения. Задача решается в несколько этапов. На каждом этапе необходимо распознать тип функции и применить соответствующее правило дифференцирования. Возможны следующие типы функций.
1. Функция имеет вид 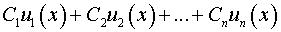 ,
,
где 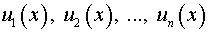 – некоторые функции и
– некоторые функции и 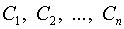 – некоторые постоянные (константы). Используем формулу производной линейной комбинации
– некоторые постоянные (константы). Используем формулу производной линейной комбинации
.
2. Функция имеет вид 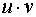 . Используем формулу производной произведения:
. Используем формулу производной произведения:
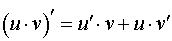 .
.
3. Функция имеет вид |
. Используем формулу производной частного: |
.
4. Функция имеет вид 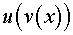 . Используем формулу производной сложной функции:
. Используем формулу производной сложной функции:
15

.
5. Функция имеет вид 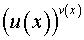 . Производная такой функции вычисляется при помощи формулы
. Производная такой функции вычисляется при помощи формулы
 .
.
Переход от этапа к этапу совершается до тех пор, пока под каждым знаком производной не окажется табличная функция.
Таблица производных основных элементарных функций.
Функция
Производная
16

Задача 5. Найти производную.
.
Задача 5. Найти производную. |
|
|
|
|
|
|
||||
|
2 3x3 4 |
|
x 2 |
|
|
|
2x2 1 |
|
|
|
5.1. y |
x2 |
. |
5.2. |
y |
1 x2 |
. |
||||
|
|
|
3x3 |
|
||||||
|
15 1 x |
|
|
|
|
|
||||
17

5.3. y |
x4 8x2 |
|
|
. |
|
|
2 x2 4 |
|
|
|
|||
|
1 x8 |
|
|
|
|
|
5.5. y |
1 x8 . |
|||||
|
12x12 |
|||||
|
x2 6 |
|
|
|
. |
|
5.7. y |
|
|
4 x2 3 |
|||
|
120x5 |
|||||
5.9. y |
|
|
4 3x3 |
|
|
. |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
x 3 2 x3 2 |
|
||||||||||||
|
|
|
|
||||||||||
5.11. y |
x6 |
x3 2 |
. |
||||||||||
|
|
|
|
|
|
|
|
||||||
|
|
1 x3 |
|||||||||||
|
|
|
|
|
|
|
|
||||||
5.13. y |
|
1 x2 |
|
|
|
||||||||
|
|
|
|
|
. |
|
|
||||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
||||||||||
|
|
|
2 |
1 2x2 |
|
|
|
||||||
5.15. y 
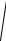 1 x2 3 .
1 x2 3 .
3x3
5.17.y 
 2x 3 x 2 .
2x 3 x 2 .
x2
5.19. y 2x2 3 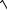
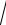 x2 3 .
x2 3 .
9x3
5.21.y 2x 1 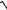
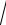 x2 x .
x2 x .
x2
5.23. |
y |
|
1 |
|
. |
|
|
|
|
||||
x 2 |
|
|
||||
x2 4x 5 |
||||||
|
|
|
|
5.4. y |
2x2 x 1 |
. |
|||||||
|
|
|
|
|
|
|
|
||
3 |
|
|
2 4x |
||||||
|
|
|
|
||||||
5.6. y |
|
|
|
x2 |
|
|
. |
||
|
|
|
|
|
|
||||
|
1 |
|
|||||||
|
2 |
3x4 |
|
||||||
5.8. y x2 8 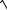
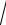 x2 8 .
x2 8 .
6x3
5.10. y 3 1 x3 4 2 .
4 2 .
x3 2
5.12. y x2 2 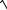
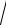 4 x2 .
4 x2 .
24x3
5.14. y 
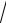 x 1 3x 2 .
x 1 3x 2 .
4x2
5.16. y x6 8x3 128 .
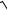 8 x3
8 x3
5.18. y 1 x2 5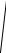 x3 1x .
x3 1x .
5.20. y |
|
x 1 |
|
. |
|||||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
x2 5 |
|
|
|
|
x2 5 |
||||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||
|
|
1 |
|
|
|
|
|
|
|
5.22. y 2 |
x |
|
. |
|
|
||||
1 |
|
|
|
|
|||||
|
|
|
|||||||
|
|
x |
|
|
|||||
5.24.y 3 3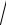 x2 x 1 .
x2 x 1 .
x1
18
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
5.25. y 3 |
|
|
x 1 |
5.26. y |
|
|
|
x 7 |
|
|
|||||||||||||||||
3 |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||||
|
|
x 1 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
6 x |
2 |
|
2x 7 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
5.27. y |
x |
|
x 1 |
|
. |
|
|
|
5.28. y |
|
x2 |
2 |
|
|
|
|
. |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
x2 |
x 1 |
|
|
|
2 1 |
x4 |
|
|
||||||||||||||||||
5.29. y x 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
2x 1 . |
|
3x |
|
|
|
|
|
|
|
||||||||||||||||||
5.30. y |
|
|
x |
|
. |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
2x 7 |
|
|
|
|
x2 2 |
|
|
||||||||||||||||
5.31. y 3x6 4x4 x2 2 .
15
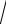 1 x2
1 x2
Дифференцирование. Задача 6
Вычисление производных
Постановка задачи. Найти производную функции 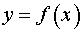 .
.
План решения. Задача решается в несколько этапов. На каждом этапе необходимо распознать тип функции и применить соответствующее правило дифференцирования. Возможны следующие типы функций.
1. Функция имеет вид 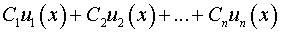 ,
,
где 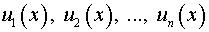 – некоторые функции и
– некоторые функции и 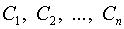 – некоторые постоянные (константы). Используем формулу производной линейной комбинации
– некоторые постоянные (константы). Используем формулу производной линейной комбинации
.
2. Функция имеет вид 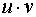 . Используем формулу производной произведения:
. Используем формулу производной произведения:
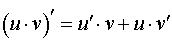 .
.
3. Функция имеет вид |
. Используем формулу производной частного: |
19

.
4. Функция имеет вид 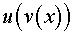 . Используем формулу производной сложной функции:
. Используем формулу производной сложной функции:
.
5. Функция имеет вид 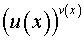 . Производная такой функции вычисляется при помощи формулы
. Производная такой функции вычисляется при помощи формулы
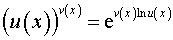 .
.
Переход от этапа к этапу совершается до тех пор, пока под каждым знаком производной не окажется табличная функция.
Таблица производных основных элементарных функций.
Функция
Производная
20
