
- •10. Применение фундаментальных законов природы (второй закон Ньютона) к построению модели колебаний системы «шарик – пружина»
- •11. Второй способ моделирования колебаний механической системы «шарик – пружина» используя закон сохранения энергии.
- •12. Третий способ построения модели колебаний механической системы «шарик – пружина» с помощью вариационного метода.
- •13. Моделирование колебаний электрического контура. Аналогия моделей
- •9. Необходимое и достаточное условие интегрируемости функций. Классы интегрируемых функций.
- •2) Достаточность . Т.К. Для т справедливы неравенства , согласно условию теоремы, можно указать такое разбиение, что . В силу произвольности .
- •10. Теорема о среднем значении определенного интеграла
- •12. Функции нескольких переменных. Предел функции многих переменных.
- •Функция деструктора
- •Конструкторы производного класса
- •Виртуальные, дружественные, статические функции. Указатель this.
- •Решения методом Фурье краевой задачи неоднородного уравнения
- •Уравнения теплопроводности. Задача Коши. Формула Пуассона
- •Дифференциальные уравнения
-
Решения методом Фурье краевой задачи неоднородного уравнения
Решение начально-краевой задачи с неоднородным волновым уравнением (уравнением теплопроводности) и нулевыми краевыми и начальными данными методом представления решения в виде ряда по собственным функциям задачи Штурма-Лиувилля.
![]()
![]() .
Решение задачи (1)(2)(3) будем писать в виде
ряда:
.
Решение задачи (1)(2)(3) будем писать в виде
ряда:
![]() .При
таком поиске решений граничные условия
выполняются автоматически.
.При
таком поиске решений граничные условия
выполняются автоматически.
![]()
![]() Подставим
(4) и (5) в уравнение (1), тогда получаем:
Подставим
(4) и (5) в уравнение (1), тогда получаем:
![]()
![]() -
ЛНДУ 1 порядка с постоянными коэффициентами.
-
ЛНДУ 1 порядка с постоянными коэффициентами.
![]()
![]()
![]() .
Найдем
.
Найдем
![]() :
:
![]()
![]()
![]()
![]()
![]() .
Согласно выражению (4)
.
Согласно выражению (4)
![]() :
:
![]() .
Найдем
.
Найдем
![]() из начальных условий:
из начальных условий:
![]()
Подставляя в (4) в решение (6), получим:
![]()
![]()
.
-
Уравнения теплопроводности. Задача Коши. Формула Пуассона
Опр. Уравнением теплопроводности называется уравнение вида:
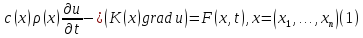
в
котором
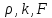 – заданные функции, а
– заданные функции, а
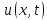 -
искомая функция и для функции
-
искомая функция и для функции
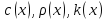 – выполнены условия
– выполнены условия
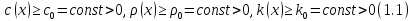
В случае, когда пространство x одномерно, уравнение принимает вид:

Если
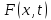 =0,
то уравнение (1) наз-ся однородным, в
противном случае – неоднородным.
=0,
то уравнение (1) наз-ся однородным, в
противном случае – неоднородным.
Уравнение (1) описывает, в частности, распространение тепла в тонком стержне, тонкой мембране или обьемном теле, диффузию вещества. На примере распространения тепла в тонком стержне рассмотрим смысл всех входящих в уравнение функций.
-
искомая функция u(x,t)представляет собой температуру стержня в точке x в момент времени t
-
функция
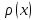 имеет смысл линейной плотности стержня
имеет смысл линейной плотности стержня -
функция k(x) – коэффициент теплопроводности в точке x
-
функция c(x) – удельная теплоёмкость
-
функция F(x,t) – наз-ся «правой « частью и представляет собой плотность источников тепла
В
простейшем случае, когда
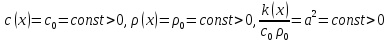 уравнение
принимает вид
уравнение
принимает вид
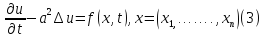
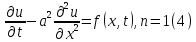
где
функция
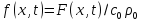
Замечание: Уравнение (3)-(4) также часто называют уравнением теплопроводности.
Опр: Задачей Коши для Уравнение теплопроводности называется задача:
Найти
функцию
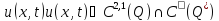 из условий:
из условий:
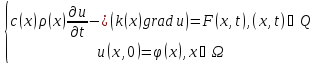 (5)
(5)
,
где
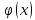 – заданная функция, называемая начальными
данными или данными Коши, а для заданных
функций
– заданная функция, называемая начальными
данными или данными Коши, а для заданных
функций
 выполнены условия (1.1) и :
выполнены условия (1.1) и :
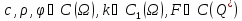
Формула
Пуассона - формула, дающая интегральное
представление решения задачи Коши для
волнового уравнения в пространстве
![]() :
:
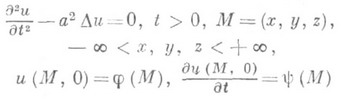
и
имеющая вид
![]()
![]() -
среднее значение функции j на сфере
-
среднее значение функции j на сфере
 в пространстве ( х, у, z) радиуса at с центром
в точке М, dW- элемент площади единичной
сферы.
в пространстве ( х, у, z) радиуса at с центром
в точке М, dW- элемент площади единичной
сферы.
3)
Иногда формулу Пуассона наз. интегральное
представление решения задачи Коши для
уравнения теплопроводности в пространстве
![]() :
:
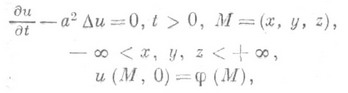 имеющее
вид
имеющее
вид
Дифференциальные уравнения
9.
Интегрирование уравнений
10. Уравнения n-го порядка, допускающие понижения порядка
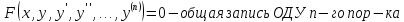
1
сл.
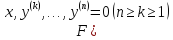 – в
– в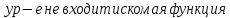
Замена
: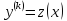
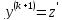


2сл.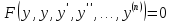 – в ур-е не входит явно независимая
переменная
– в ур-е не входит явно независимая
переменная
Замена:
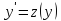
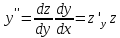
Чтобы
заменить
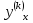 ,
надо продифференцировать по x
выражение
,
надо продифференцировать по x
выражение
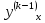 через
через
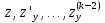 .
Для этого надо его продифференцировать
по y
и затем умножить на
.
Для этого надо его продифференцировать
по y
и затем умножить на
 ,
т.е. на z.
Получим выражение
,
т.е. на z.
Получим выражение
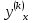 через
через
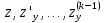 .
.
 – порядок
уравнения понижается на ед-цу
– порядок
уравнения понижается на ед-цу
3
сл. Если ОДУ однородно относительно
 ,
то порядок уравнения можно понизить
через замену
,
то порядок уравнения можно понизить
через замену
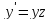 ,
где z-неизвестная
новая переменная.
,
где z-неизвестная
новая переменная.
Замена:

Выражение
для каждой производной
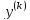 получается путем дифференцирования
выражения для
получается путем дифференцирования
выражения для
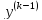 и замены y’
на yz.
После подстановки этих выражений в
уравнение производится сокращение на
y
и получается уравнение порядка n-1
относительно z.
и замены y’
на yz.
После подстановки этих выражений в
уравнение производится сокращение на
y
и получается уравнение порядка n-1
относительно z.
4
сл. Если дифференциальное уравнение
относительно x,y
в общем смысле, то делается замена: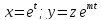
после
которой порядок уравнения понзим по
второму случаю: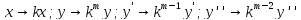 .
Подставим в ДУ, из равенства степеней
k
каждого слагаемого находим m.
.
Подставим в ДУ, из равенства степеней
k
каждого слагаемого находим m.
5 сл. Если обе части ДУ можно представить в виде полных производных от чего-либо, то убрав производные можно понизить порядок без замены :
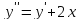
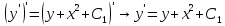
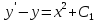
11. Дифференциальные уравнения n-го порядка. Понятие решения, общего решения.
Дифференциальным уравнением n-го порядка называется уравнение вида
F (x, y, y′, y′′, ... , y(n) ) = 0 , (3.1)
где x – независимая переменная, x∈Ω , Ω ⊆ Ρ ; y = y(x) – неизвестная функция независимой переменной x ; y′ = y′(x) ,
y′′ = y′′(x) , …, y(n) = y(n) (x) – производные неизвестной функции; F( •, •, •, •, ... , •) – некоторая заданная функция своих
аргументов.
Частным случаем уравнения (3.1) является уравнение вида
y(n) = f (x, y, y′, y′′, ... , y(n−1) ), (3.2)
которое называется уравнением, разрешённым относительно старшей производной.
Решением дифференциального уравнения n-го порядка называется n раз непрерывно дифференцируемая на множестве
Ω функция y = ϕ(x) , при подстановке которой в уравнение получается тождество относительно независимой переменной
x∈Ω .
Общее решение дифференциального уравнения, заданное в неявном виде
Φ(x, y,C1,C2 , ... , Cn ) = 0 ,
называют общим интегралом этого уравнения.
Частным решением дифференциального уравнения n-го порядка называется его решение, которое получается из общего
решения
этого уравнения при конкретных значениях
параметров C1
=
C1
*, C2
=
C2*
, …, Cn
=
Cn*
(С1*,С2*,…,Сn*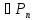 )
)
Частное
решение дифференциального уравнения,
заданное в неявном виде
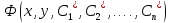 ,
называют частныминтегралом
этого
уравнения.
,
называют частныминтегралом
этого
уравнения.
12. Фундаментальная система решений. Свойства решений линейных однородных дифференциальных уравнений
Опр. Линейным дифференциальным уравнением n-го порядка называется уравнение, в которое неизвестная функция y(x) и её производные входят линейно, т.е. в первой степени:
![]() ;
;
Опр.Фундаментальной системой решений линейного однородного дифференциального уравнения n-го порядка называется любая линейно независимая система y1(x), y2(x), …, yn(x) его n частных решений.
Теорема (о структуре общего решения линейного однородного дифференциального уравнения.) Общее решение y(x) линейного однородного дифференциального уравнения есть линейная комбинация функций из фундаментальной системы решений этого уравнения:
y(x) = C1 y1(x) + C2 y2(x) + …+ Cn yn(x).
Док-во.
Пусть y1(x),
y2(x),
…, yn(x)
- фундаментальная система решений
линейного однородного дифференциального
уравнения. Требуется доказать, что любое
частное решение yчо(x)
этого уравнения содержится в формуле
y(x)
= C1
y1(x)
+ C2
y2(x)
+ …+ Cn
yn(x)
при некотором наборе постоянных C1,
C2,
…, Cn.
Возьмём любую точку
![]() , вычислим в этой точке числа
, вычислим в этой точке числа
![]() и найдём постоянные C1,
C2,
…, Cn
как решение линейной неоднородной
системы алгебраических уравнений
и найдём постоянные C1,
C2,
…, Cn
как решение линейной неоднородной
системы алгебраических уравнений
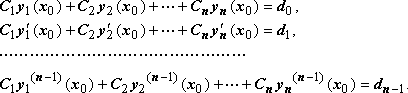
Такое
решение существует и единственно, так
как определитель этой системы равен
![]() .
Рассмотрим линейную комбинацию y(x)
= C1
y1(x)
+ C2
y2(x)
+ …+ Cn
yn(x)
функций из фундаментальной системы
решений с этими значениями постоянных
C1,
C2,
…, Cn
и сравним её с функцией yчо(x).
Функции y(x)
и yчо(x)
удовлетворяют одному уравнению и
одинаковым начальным условиям в точке
x0,
следовательно, по единственности решения
задачи Коши, они совпадают: yчо(x)
= C1
y1(x)
+ C2
y2(x)
+ … + Cn
yn(x).
Теорема доказана.
.
Рассмотрим линейную комбинацию y(x)
= C1
y1(x)
+ C2
y2(x)
+ …+ Cn
yn(x)
функций из фундаментальной системы
решений с этими значениями постоянных
C1,
C2,
…, Cn
и сравним её с функцией yчо(x).
Функции y(x)
и yчо(x)
удовлетворяют одному уравнению и
одинаковым начальным условиям в точке
x0,
следовательно, по единственности решения
задачи Коши, они совпадают: yчо(x)
= C1
y1(x)
+ C2
y2(x)
+ … + Cn
yn(x).
Теорема доказана.
Из этой теоремы следует, что размерность линейного пространства частных решений однородного уравнения с непрерывными коэффициентами не превышает n. Осталось доказать, что эта размерность не меньше n.
Для линейного однородного дифференциального уравнения n-го порядка
y(n) + a1(x) y(n-1) + ... + an-1 (x) y' + an(x) y = 0,
где y = y(x) — неизвестная функция, a1(x), a2(x), ..., an-1(x), an(x) — известные, непрерывные, справедливо:
1) существуют n линейно независимых решений уравнения
y1(x), y2(x), ..., yn(x);
2) при любых значениях констант c1, c2, ..., cn функция
y(x)= c1 y1(x) + c2 y2(x) + ... + cn yn(x)
является решением уравнения;
3) для любых начальных значений x0, y0, y0,1, ..., y0,n-1 существуют такие значения c*1, c*n, ..., c*n, что решение
y*(x)=c*1 y1(x) + c*2 y2(x) + ... + c*n yn (x)
удовлетворяет при x = x0 начальным условиям
y*(x0)=y0, (y*)'(x0)=y0,1 , ...,(y*)(n-1)(x0)=y0,n-1.
13. Свойства решений линейных неоднородных дифференциальных уравнений
Опр. Линейным неоднородным дифференциальным уравнением (ЛНДУ) n-го порядка называется уравнение вида :

Опр. Система n линейно независимых частных решений дифференциального уравнения n-го порядка называется фундаментальной системой частных решений этого дифференциального уравнения.
Свойства решений линейных неоднородных ДУ:
1.если
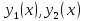 – два решения неоднородного уравнения,
то функция
– два решения неоднородного уравнения,
то функция
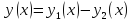 – решение соответствующего однородного
уравнения
– решение соответствующего однородного
уравнения
2.
если
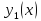 –
решение неоднородного уравнения,
–
решение неоднородного уравнения,
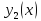 –
решение однородного уравнения, то
функция
–
решение однородного уравнения, то
функция
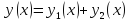 – решение неоднородного уравнения
– решение неоднородного уравнения
3.
если
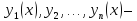 —
n линейно независимых решений однородного
уравнения, а
—
n линейно независимых решений однородного
уравнения, а
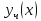 –
— произвольное решение неоднородного
уравнения, то для любых начальных
значений
–
— произвольное решение неоднородного
уравнения, то для любых начальных
значений
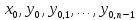
Существуют
такие значения
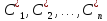 ,
что решение
,
что решение
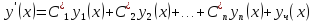
удовлетворяет при x = x0 начальным условиям
y*(x0)=y0, (y*)'(x0)=y0,1 , ...,(y*)(n-1)(x0)=y0,n-1.
Выражение
y(x)= c1 y1(x) + c2 y2(x) + ... + cn yn(x) + yч(x)
называется общим решением линейного неоднородного дифференциального уравнения n-го порядка.
Для отыскания частных решений неоднородных дифференциальных уравнений с постоянными коэффициентами с правыми частями вида:
Pk(x)exp(ax)cos(bx) + Qm(x)exp(ax)sin(bx),
где Pk(x), Qm(x) — многочлены степени k и m соответственно, существует простой алгоритм построения частного решения, называемый методом подбора.
