9. Виртуальные, дружественные, статические функции. Указатель this.

Виртуальные функции

Функции-элементы класса могут объявляться в C++ как виртуальные. Ключевое слово virtual заставляет компилятор генерировать для класса некоторую дополнительную информацию 6 функции. Происходит следующее: если виртуальная функция переопределяется в производном классе, и если имеется указатель или ссылка на базовый класс (которые могут с тем же успехом ссылаться на производный класс, поскольку производный объект есть в то же время и объект базового класса), то при обращении к функции через указатель (ссылку) будет вызвана правильная функция-элемент (т. е. соответствующая типу действительного объекта) — базового или одного из производных классов, в зависимости от типа конкретного объекта.

Дружественная функция

Дружественные функции применяются для доступа к скрытым полям класса и представляют собой альтернативу методам. Метод, как правило, описывает свойство объекта, а в виде дружественных функций оформляются действия, не являющиеся свойствами класса, но концептуально входящие в его интерфейс и нуждающиеся в доступе к его скрытым полям, например, переопределенные операции вывода объектов.

Ниже перечислены правила описания и особенности дружественных функций.

Дружественная функция объявляется внутри класса, к элементам которого ей нужен доступ, с ключевым словом friend. В качестве параметра ей должен передаваться объект или ссылка на объект класса, поскольку указатель this ей не передается.

В качестве примера ниже приведено описание двух функций, дружественных классу monstr. Функция kill является методом класса hero, а функция steal_ammo не принадлежит ни одному классу. Обеим функциям в качестве параметра передается ссылка на объект класса monstr.

class monstr; // Предварительное объявление класса

class hero{

public:

void kill(monstr &);

... };

class monstr{ ...

friend int steal_ammo(monstr &);

friend void hero::kill(monstr &);

// Класс hero должен быть определен ранее };

int steal_ammo(monstr &M){return --M.ammo;}

void hero::kill(monstr &M){M.health = 0; M.ammo = 0;}

Статические функции-члены

Перед объявлением функции-члена класса можно поставить служебное слово static. Особенностью таких статических функций-членов является следующее: как и к статическому данному-члену класса, к ней можно обратиться еще до того, как в программе создан первый объект такого класса. Статические функции-члены (компонентные функции) позволяют получить доступ к частным статическим данным-членам класса, не имея еще ни одного объекта данного типа в программе.

Для статической компонентной функции не определен указатель this. Когда это необходимо, адрес объекта, для которого вызывается статическая функция-член, должен быть передан ей явно в виде аргумента.

Пример:

class prim{

int numb;

static stat;

public:

prim (int i) {

numb=i;

}

/* Далее - статическая функция. Указатель this не определен и выбор объекта осуществляется по явно переданному указателю.

Член stat не требует указателя на объект, .т.к. он общий для всех объектов класса prim.

*/

static void func (int i, prim *p = 0) {

if (p) p-> numb = i;

else stat = i;

}

static void show ( ){

/* Статическая функция обращается только к статическому члену класса, никаких указателей не требуется: */

cout<<"stat="< }

}; // Конец класса prim.

int prim::stat = 8; // Инициализация статического члена класса.

void main(){

/* До создания объектов типа prim возможен единственный способ обращения к статической функции-члену: */

ptim::show ();

// Можно изменить значение статического члена класса:

prim::func(10);

/* После создания объекта типа prim можно обратиться к статической функции обычным для абстрактных типов способом: */

prim obj(23); // obj.numb становится равным 23.

obj.show();

// Можно изменить значение созданного объекта:

prim::func(20, &obj); // obj.numb = = 20.

obj.func(27, &obj); // obj.numb = = 27.

}

Указатель this

Каждый объект содержит свой экземпляр полей класса. Методы класса находятся в памяти в единственном экземпляре и используются всеми объектами совместно, поэтому необходимо обеспечить работу методов с полями именно того объекта, для которого они были вызваны. Это обеспечивается передачей в функцию скрытого параметра this, в котором хранится константный указатель на вызвавший функцию объект. Указатель this неявно используется внутри метода для ссылок на элементы объекта. В явном виде этот указатель применяется в основном для возвращения из метода указателя (return this;) или ссылки (return *this;) на вызвавший объект.

Для иллюстрации использования указателя this добавим в приведенный выше класс monstr новый метод, возвращающий ссылку на наиболее здорового (поле health) из двух монстров, один из которых вызывает метод, а другой передается ему в качестве параметра (метод нужно поместить в секцию public описания класса):

monstr & the_best(monstr &M){

if( health > M.get_health()) return *this;

return M;

}

... monstr Vasia(50), Super(200);

// Новый объект Best инициализируется значениями полей Super:

Vasia.the_best(Super);

Указатель this можно также применять для идентификации поля класса в том случае, когда его имя совпадает с именем формального параметра метода. Другой способ идентификации поля использует операцию доступа к области видимости:

void cure(int health, int ammo){

this -> health += health; // Использование this

monstr:: ammo += ammo; // Использование операции ::

}

Введение в вычислительную математику

17. Первая интерполяционная формула Ньютона. Оценка погрешности

Пусть для функции равной 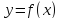заданы значения 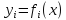для равноотстоящих значений независимой переменной: 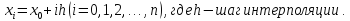Требуется подобрать полином 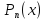степени не выше n, принимающий в точках 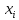значения

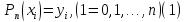
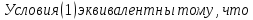
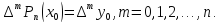
Следуя Ньютону, будем искать полином в виде

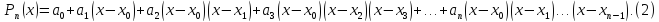
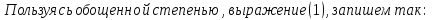
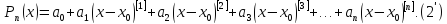
Наша задача состоит в определении коэффициентов 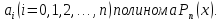полагая

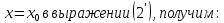
Чтобы найти коэффициент 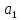, составим в первую конечную разность .

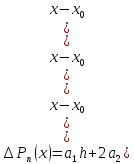Полагая в последнем выражении

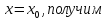
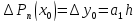
Откуда

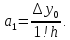
Для определения коэффициента 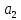составим конечную разность второго порядка

.

Полагая в последнем выражении

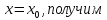
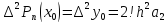
Откуда

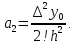
Последовательно продолжая этот процесс, мы обнаружим, что

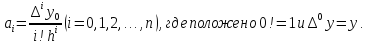
Подставляя найденные значения коэффициентов 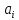в выражение (2’), получим интерполяционный полином Ньютона

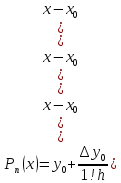
Легко видеть что полином (3) полностью удовлетворяет требованиям поставленной задачи. Действительно, во-первых, степень полинома 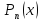не выше n, во-вторых

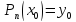
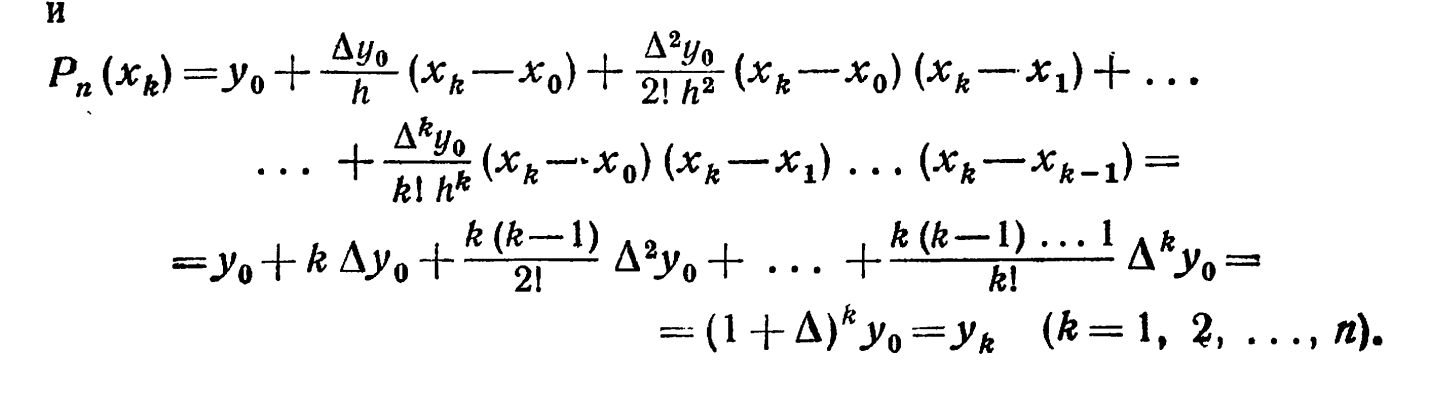
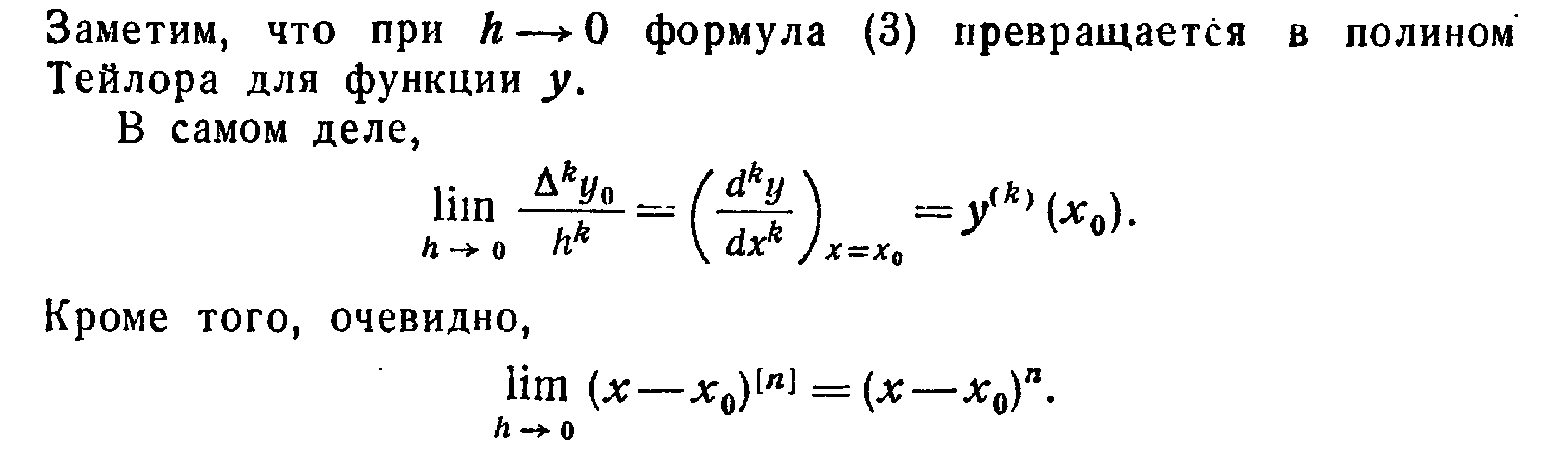
Оценка погрешности первой итерационной формулы Ньютона

18. Вторая интерполяционная формула Ньютона. Оценка погрешности.

Оценка погрешности второй интерполяционной формулы Ньютона

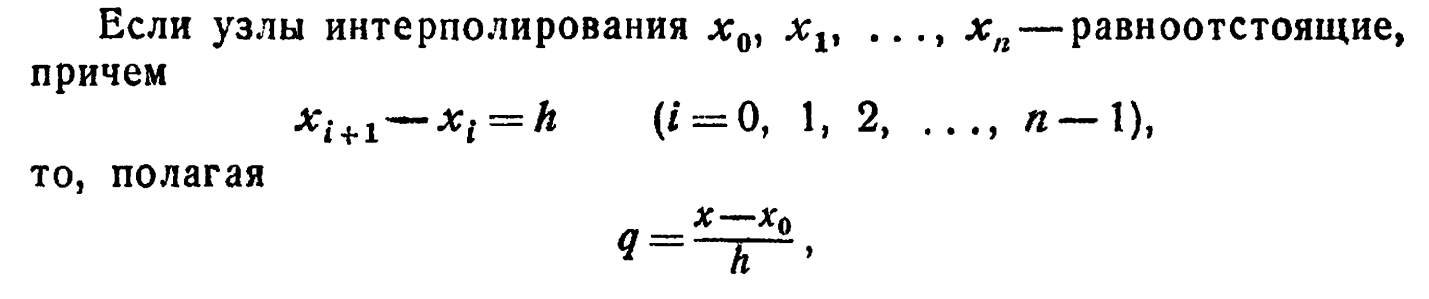
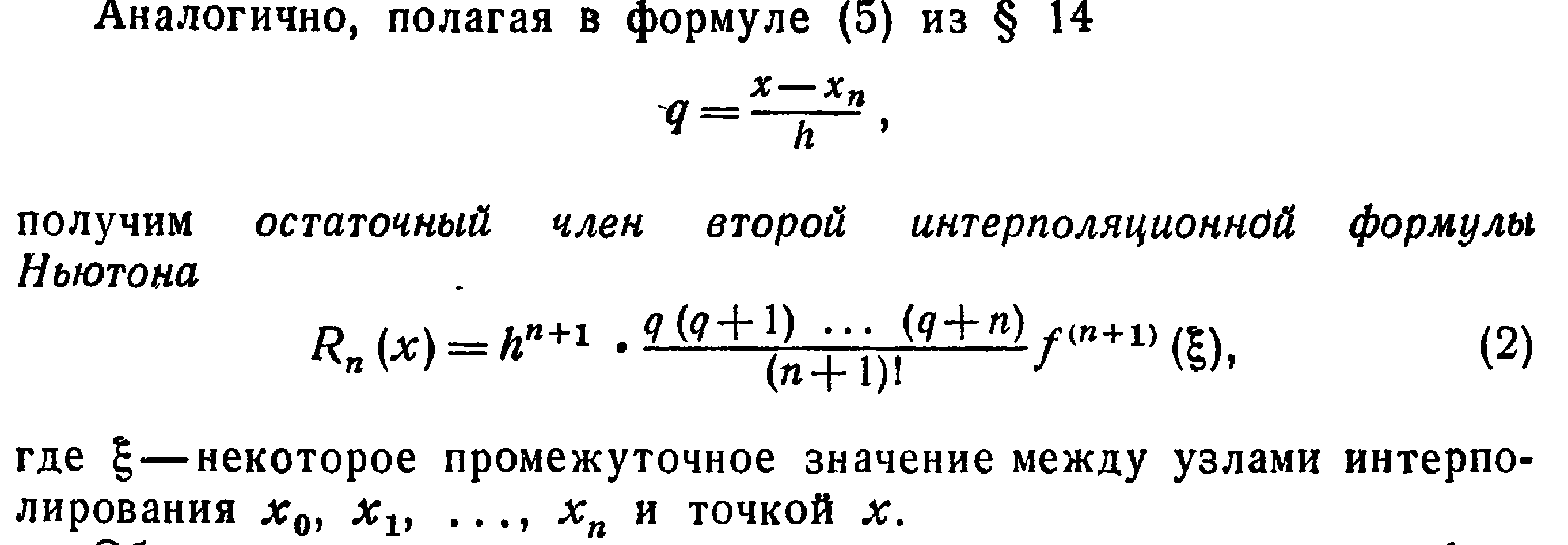
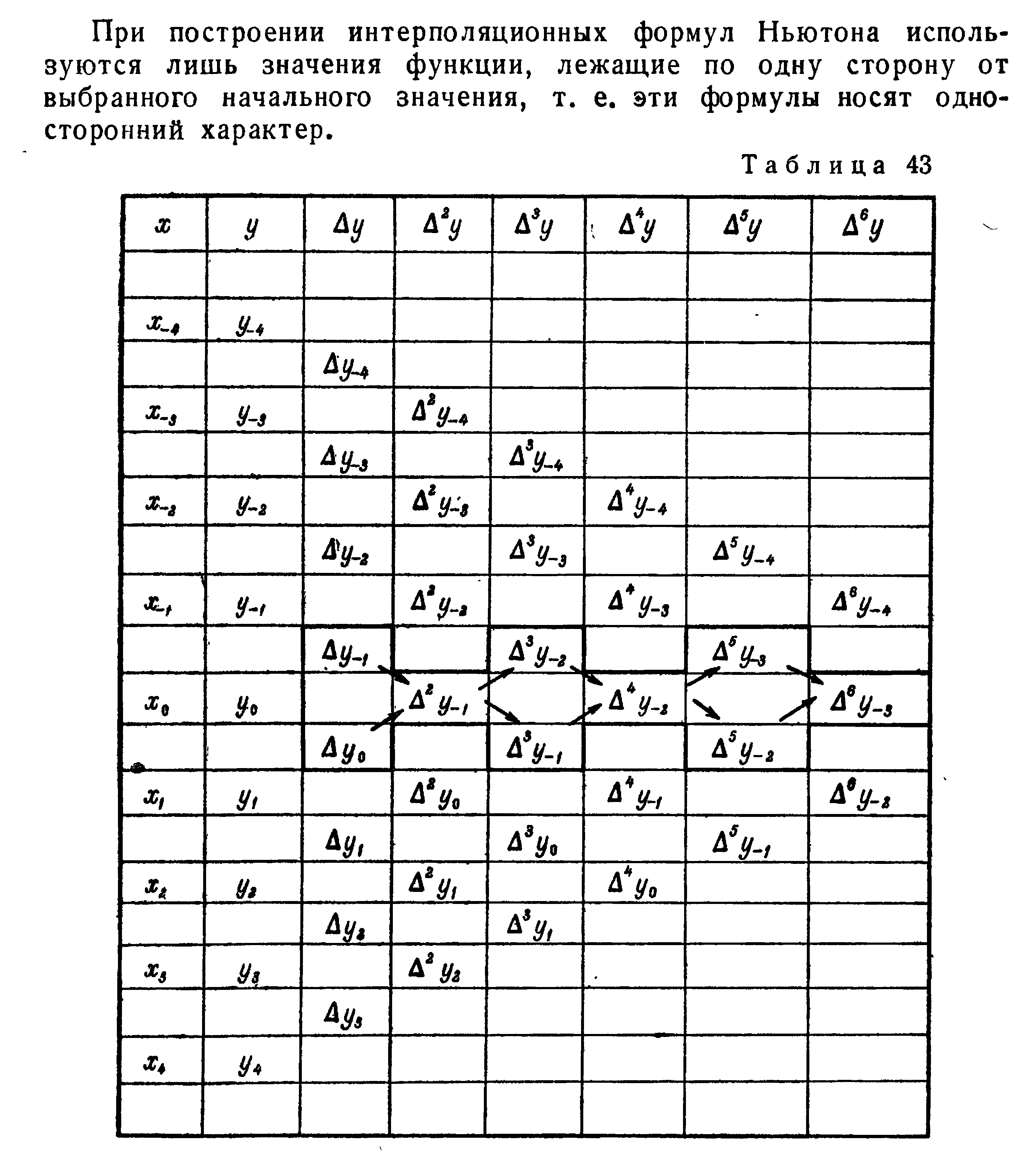
19.Таблица центральных разностей. Интерполяц. формула Гаусса. Оценка погрешности

20. Интерполяционная формула Стирлинга и Бесселя. Оценка погрешности

Интерполяционная формула Стрилинга

Интерполяционная формула Бесселя

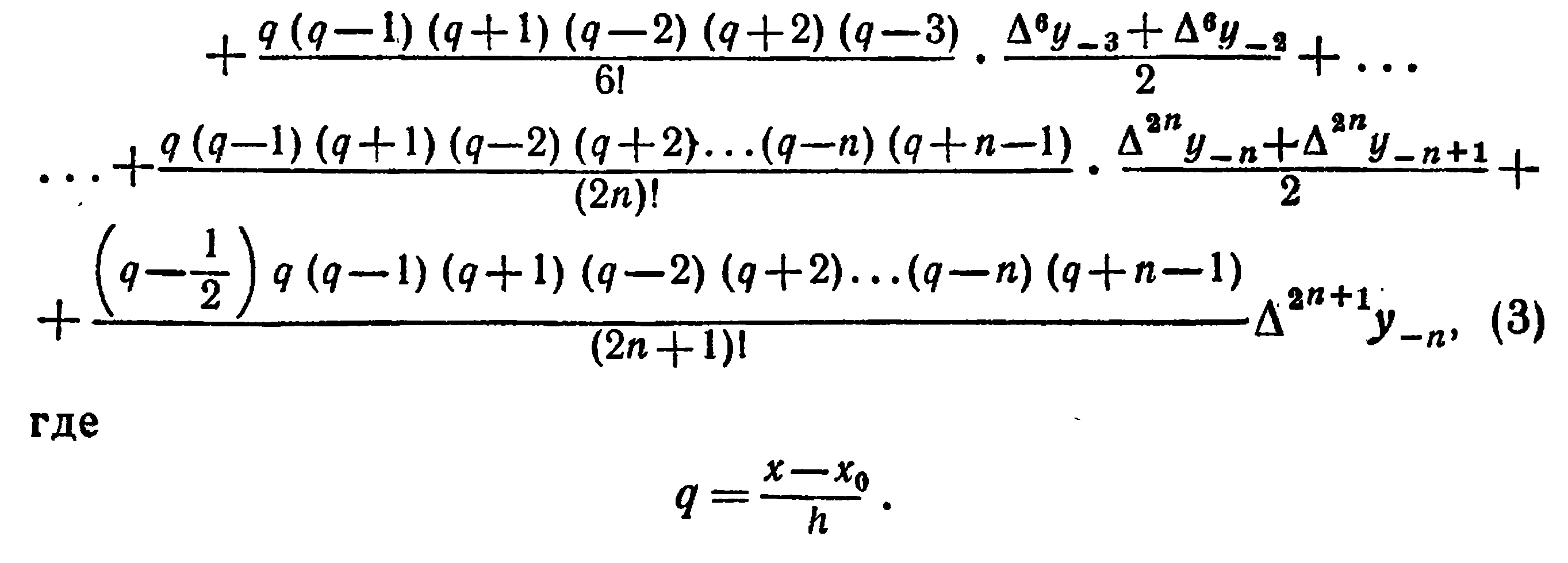
Оценки погрешностей

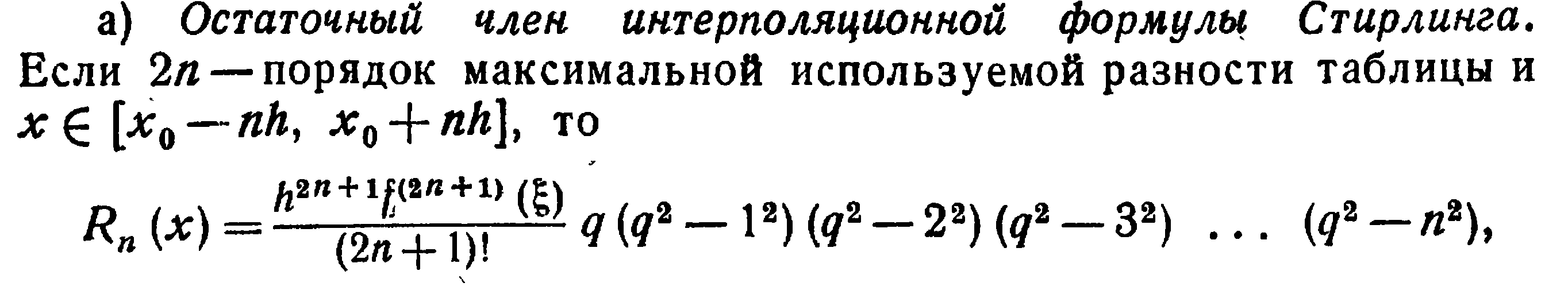
21. Интерполяционная формула Лагранжа. Оценка погрешности

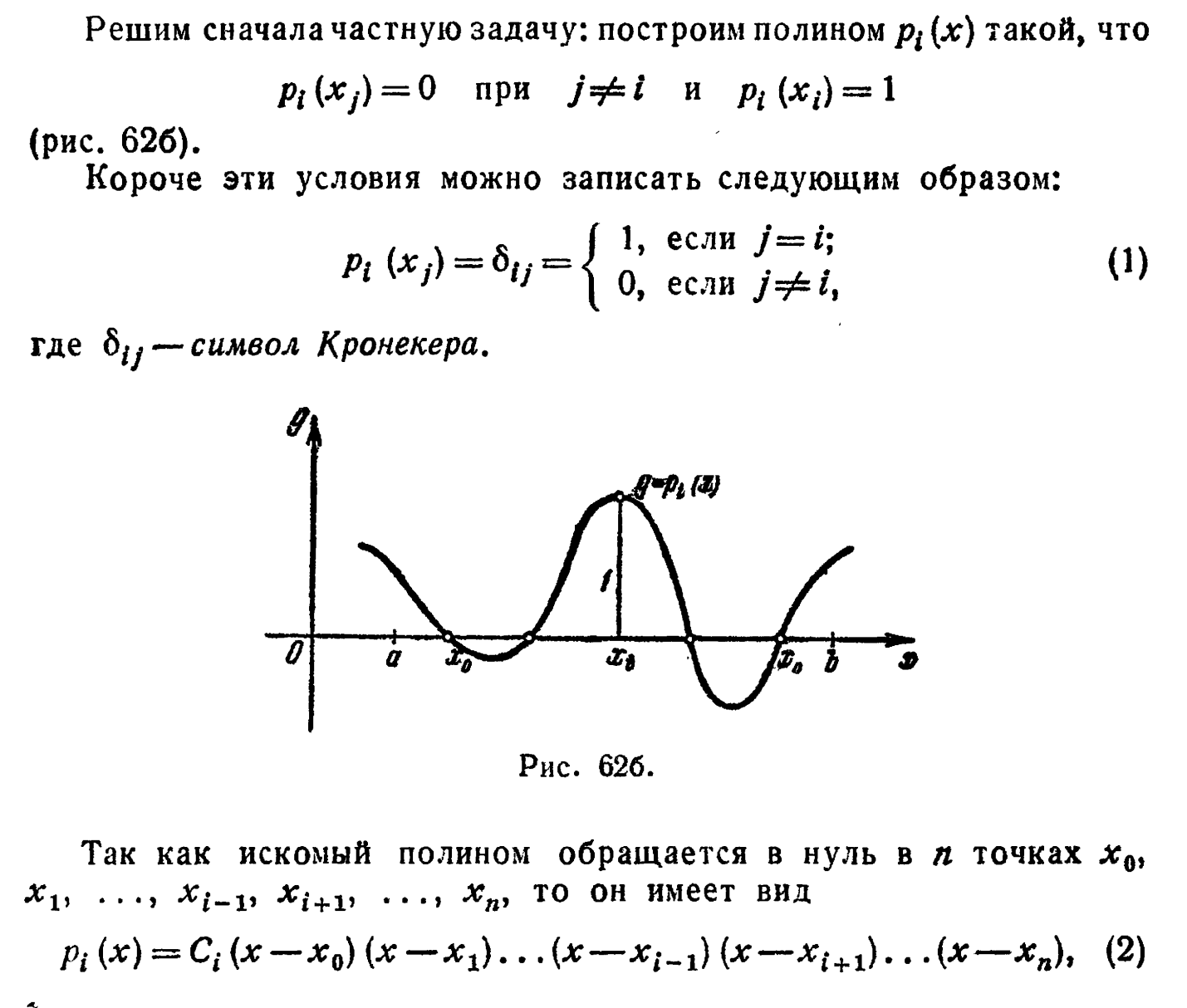
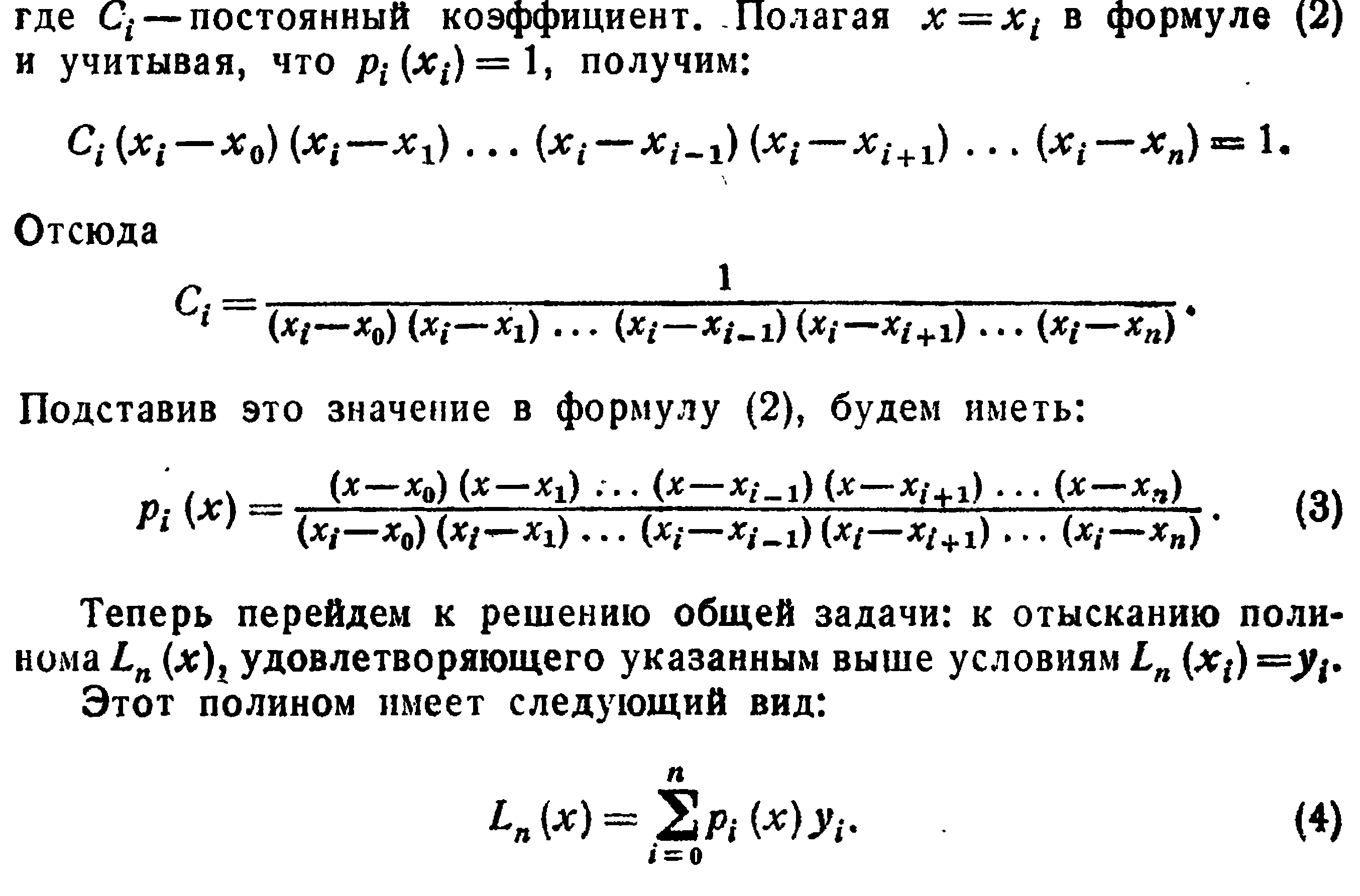
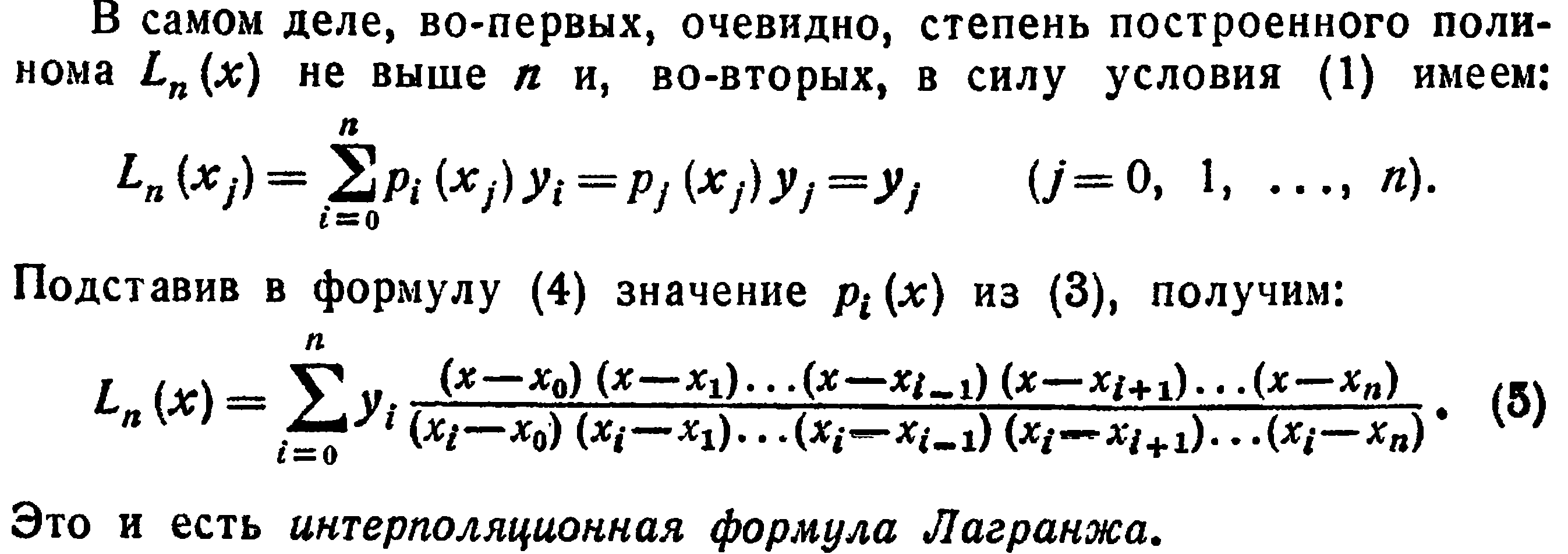
Абсолютная погрешность интерполяционной формулы Лагранжа

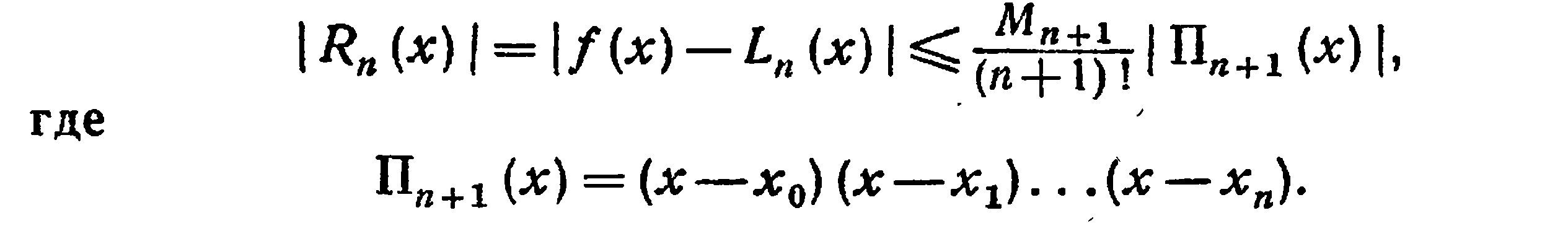
22. Обратное интерполирование. Экстраполяция Ричардсона

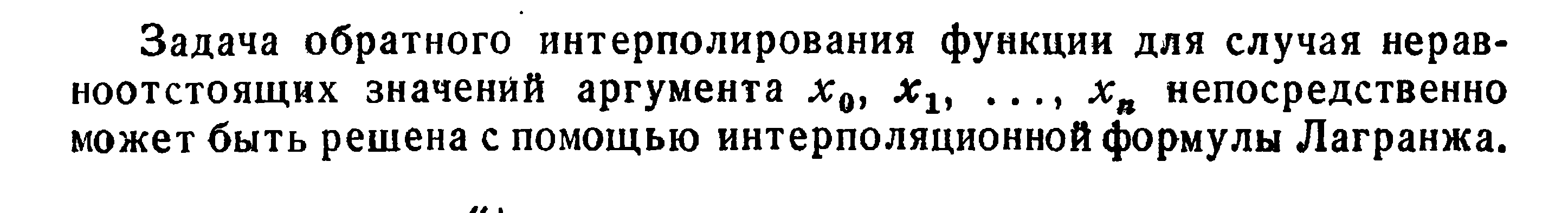
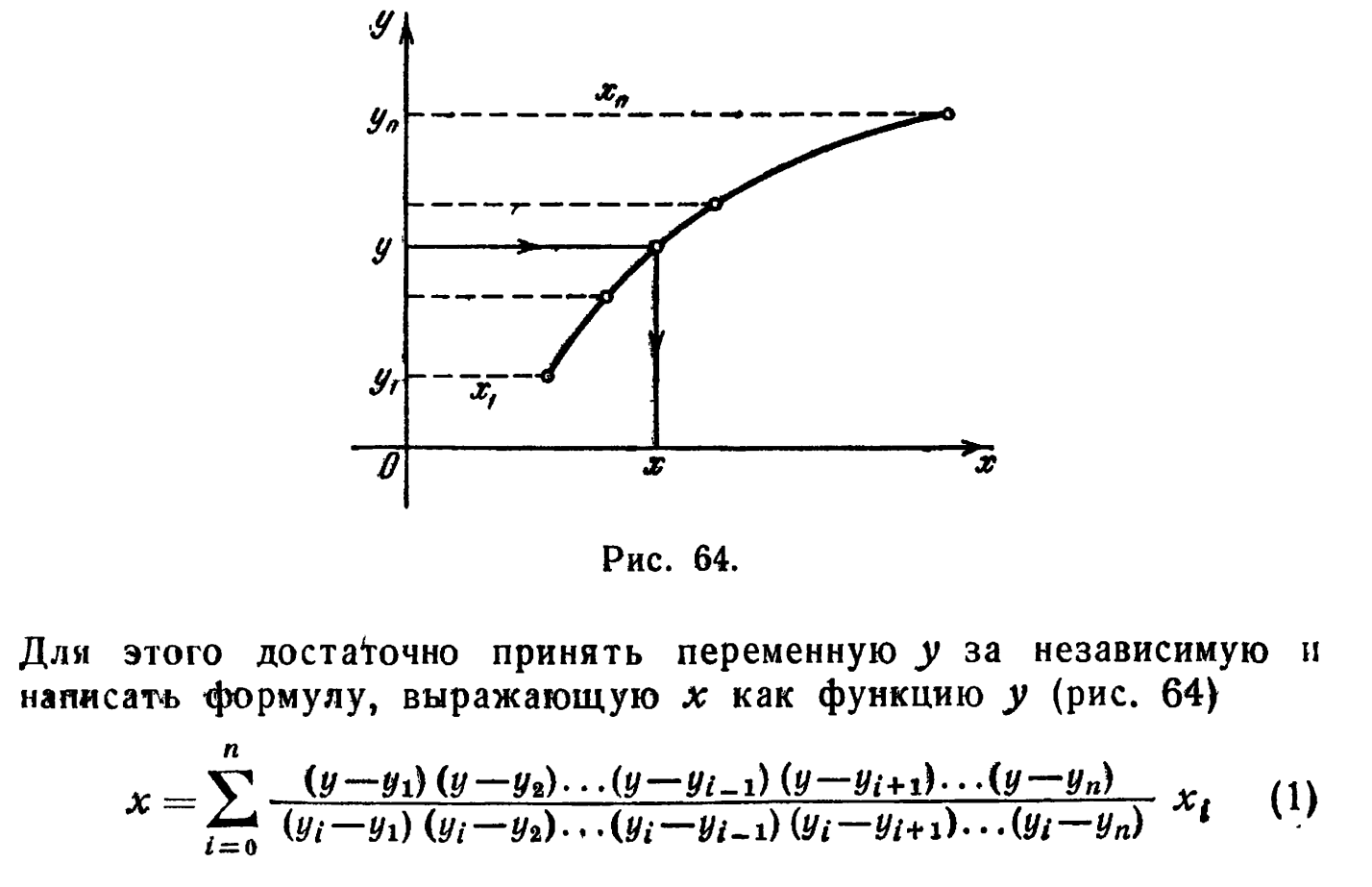
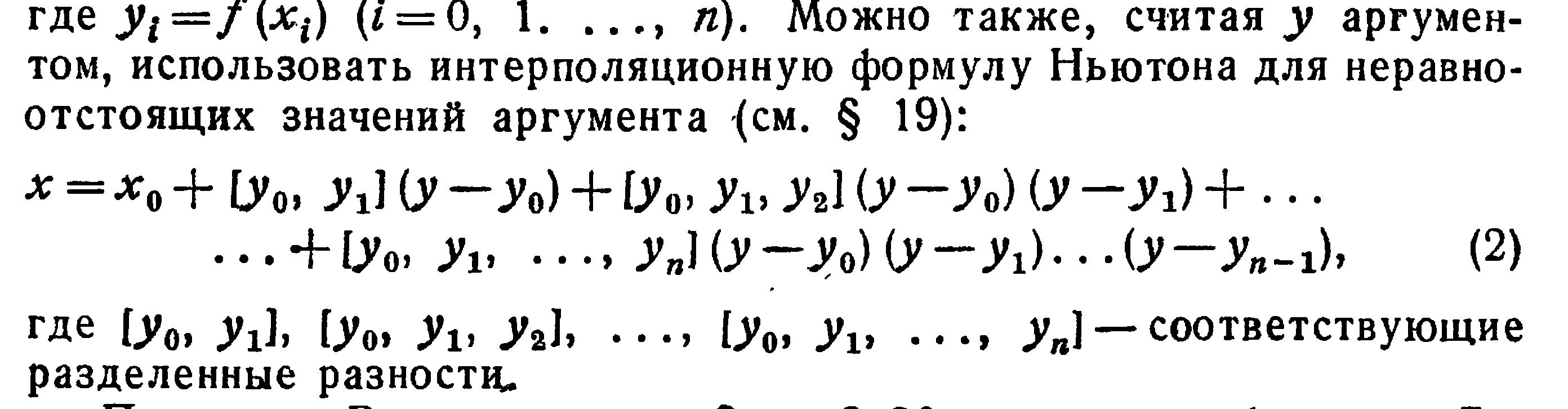
Экстраполяция Ричардсона — процедура, позволяющая получить уточненное решение по двум менее точным. Используя определение сходимости разностных схем , где — точное решение в узлах сетки, а — полученное с помощью разностной схемы, можно придти к соотношению

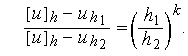
Здесь и — кратные шаги сетки, такие, что узлы более частой сетки, совпадают с узлами более редкой; и — приближенное решение, полученное в узлах более редкой сетки с соотвествующим шагом. В этом случае, если известен порядок сходимости разностной схемы , можно получить "точное" решение .

23. О наилучшем выборе узлов интерполирования. Квадратурная формула Ньютона-Котеса

УМФ

10.Единственность решения краевой задачи для волнового уравнения

Рассмотрим смешанную краевую задачу: найти функцию u(x,t) непрерывную в прямоугольнике , удовлетворяющую уpавнению :

(1) в ,

где ,

начальным условиям:

(2a) u(x,0) = φ(x), ;

(2б) ut(x,0) = ψ(x), ;

и граничным условиям:

(3)

где (так как одновременно).

Сформулируем для этой задачи теорему единственности :

Теорема: cмешанная задача (1)-(3) имеет единственное решение, если выполняется :

(A) u(x,t) - имеет непрерывные производные до второго порядка включительно в .

(B) Коэффициенты r(x), k(x), k'(x), q(x) - непрерывные функции при .

Доказательство: допустим, что существует два решения задачи (1)-(3) : u1(x,t), u2(x,t).

Рассмотрим разность этих решений: υ(x,t) = u1(x,t) - u2(x,t).

Функция υ(x,t) будет удовлетворять однородному уравнению:

(4) в G = (0,l) × (0,T)

нулевым начальным условиям

(5) .

и однородным граничным условиям

(6)

и будет удовлетворять условию (А) теоремы.

Требуется доказать, что υ(x,t) º 0 (т.е. для всех x и y из ).

Рассмотрим вспомогательную функцию :

(7) .

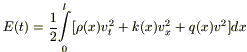Покажем, что E(t) не зависит от t .

Продифференцируем (7) по t, выполняя при этом дифференцирование под знаком интеграла [это возможно, так как 2ые производные от u(x,t) - непрерывны в (условие (А)), r, k, k', q(x)] - удовлетворяют условию (B):

.

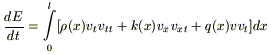Проинтегрируем средний член по частям :

.

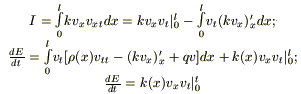Проинтегрируем полученное соотношение от t = 0 до t = t по t:

.

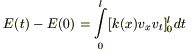Рассмотрим правую часть этого соотношения для различных типов граничных условий:

10) 1го рода: h2 = H2 =0 (дифференцируем по t) , тогда E(t) º E(0);

20)2 го рода: (h1 = H1 = 0) , тогда E(t) º E(0); Þ E(t) º E(0)

30) 3го рода: можно показать, что при граничных условиях 3го рода:

. Тогда

(*)

Покажем, что E(0) = 0.

Продифференцируем 1ое из нормальных условий по х: υx(x,0) = 0;

2ое из нормальных условий по t: υt(x,0) = 0.

Подстановка полученных значений в (7) дает, что Е(0) = 0.

Для граничных условий 1го и 2го рода это дает Е(t) º 0.

Для граничных условий 3го рода (*) , но с другой стороны, в силу определения Е(t) из (7), .

Следовательно, E(t) º 0 и при граничных условиях 3го рода.

Тогда из (7) подынтегральная функция - тождественный нуль, откуда следует, что υx(x,t) º 0; υt(x,t) º 0, т.е. υ(x,t) º const = C0 в .

В силу нормальных условий: υ(x,0) = 0, получаем, что υ(x,t) º 0, значит u1 º u2, что и требовалось доказать.

11.Решение методом Фурье краевой задачи для однородного уравнения. Собственные значения и собственные функции задачи Штурма – Лиувилля.

Метод Фурье решения начально-краевых задач для однородного волнового уравнения (уравнение теплопроводности) с однородными краевыми условиями.

Решение задач о свободных колебаниях ограниченной струны с закрепленными концами.

Метод Фурье или метод разделения переменных является одним из наиболее распространенных аналитических методов решения уравнений с частными производными. Он заключается в нахождении частных решений заданного уравнения не равных тождественно нулю в виде произведения двух функций, каждая из которых зависит только от одной переменной.

Решение задачи будем искать в виде:

. Подставляя в получаем:

- Будет выполняться при условии

, . Используя граничные условия, получим:

Собственные значения и собственные функции задачи Ш-Л.

Будем рассматривать однородное линейное уравнение второго порядка

Ly ≡ a2(x)y'' + a1(x)y' + a0(x)y = 0.

Его можно записать по-другому: (15)

Однородное уравнение Ly = 0 и неоднородное Ly = f, как известно, имеют бесконечное множество решений. На практике часто бывает нужно из множества решений выделить только одно. Для этого задают некоторые дополнительные условия. Если это начальные условия у(х0) = уo, y'(xo) = y1, то получают задачу Коши. Если задают дополнительные условия на концах некоторого отрезка, то получают задачу, которая называется краевой задачей. Условия, которые задаются на концах отрезка, называются краевыми условиями. Краевые условия иногда именуют также граничными условиями и тогда говорят о граничной задаче.

Мы будем задавать линейные краевые условия вида 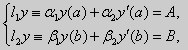(16)

где α1, α2, β1, β2, A, B - заданные числа, причем по крайней мере одно из чисел α1, α2, и одно из чисел β1, β2, отличны от нуля. Если в (16) хотя бы одно из чисел А и В не равно нулю, то краевые условия называют неоднородными. Если А = В = 0, то условия (16) называются однородными. Краевая задача называется однородной, если рассматривается однородное уравнение (15) Ly = 0 и однородные краевые условия (16).

Наряду с уравнением (15) рассмотрим уравнение (17)

содержащее некоторый числовой параметр λ. Здесь функции р(х), q(x), r(x) действительные, а число λ может быть, вообще говоря, и комплексным. Краевая задача (17), (16) при А = В = 0 является однородной.

Задача Штурма-Лиувилля. Найти те значения параметра λ, при которых уравнение (17) имеет нетривиальное решение, удовлетворяюшее однородным краевым условиям (16). В дальнейшем будем ее записывать в виде

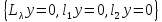
Те значения параметра λ, при которых задача Штурма-Лиувилля имеет ненулевое решение, называются собственными значениями (собственными числами) задачи, а сами эти решения - собственными функциями. Задачу Штурма-Лиувилля называют также задачей на собственные значения

Общая задача Штурма-Лиувилля будет обладать свойствами, очень похожими на свойства в этих простых случаях, если на коэффициенты уравнения (17) наложить дополнительные условия: р(х), q(x), f(x) -непрерывные функции, причем р(х) имеет, кроме того, непрерывную производную на [а, b], р(х) > 0, q(x) ≥ 0.

Основные свойства собственных значений и собственных функций задачи Штурма-Лиувилля.

Лемма. Определитель Вронского двух собственных функций задачи Штурма-Лиувилля на концах отрезка [а, b] равен нулю.

Свойство 1. Две собственные функции задачи Штурма-Лиувилля, соответствующие одному и тому же собственному значению λ, линейно зависимые.

Свойство 2. Две собственные функции у1(x) и у2(x), соответствующие различным собственным значениям λ1 и λ2 (λ1 ≠ λ2), на отрезке [а, b] ортогональны.

Свойство 3. Собственные функции, соответствующие различным собственным значениям, образуют линейно независимую систему функций.

Свойство 4. Собственные значения задачи Штурма-Лиувилля действительные.

Свойство 5. Пусть коэффициенты уравнения (17) удовлетворяют условиям: р(х), q(x), r(x) - непрерывные функции и, кроме того, р(х) имеет непрерывную производную на [а, b], р(х) > 0, q(x) > 0, r(х) > 0. Тогда задача Штурма-Лиувилля {Lλ y = 0, l1 y = 0, l2 y = 0} имеет бесконечное число собственных значений λ 1, λ2, ... λn, ... Если краевые условия имеют вид (19) или (20), или (21), то собственные значения соответствующей задачи Штурма-Лиувилля удовлетворяют неравенствам