13. Моделирование колебаний электрического контура. Аналогия моделей

Это устройство представляет собой конденсатор, соединенный проводами с индуктивной катушкой. В момент t=0 цепь замыкается, и заряд с обкладок конденсатора начинает распространяться по цепи.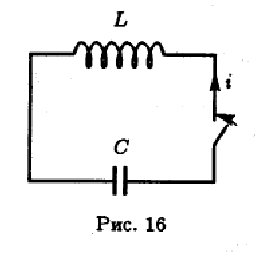

Сопротивление проводов будем считать равным нулю, емкость конденсатора равна С, индуктивность катушки L. Для изменяющейся со временем величины q(t), где q(t) – заряд на обкладках конденсатора, необходимо получить соответствующее уравнение. Очевидно, что ток i(t) и напряжение v(t) также являются функциями времени.

По физическому смыслу величины С в любой момент времени имеем равенство v(t)=q(t)С (емкость равна величине заряда, который необходимо поместить на обкладки конденсатора для увеличения разности потенциалов между ними на единицу).

Так как электрическое сопротивление в цепи отсутствует, то падения напряжения на проводах нет, и разность потенциалов v(t), существующая на конденсаторе, подается непосредственно на катушку. При переменном токе в катушке возникает электродвижущая сила самоиндукции, равная

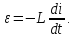
Закон Ома для цепи в отсутствие сопротивления выглядит следующим образом:

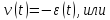
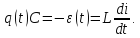
Так как по определению 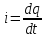( при изменении заряда на конденсаторе в цепи возникает ток), то из последнего соотношения получаем уравнение

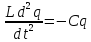
описывающее процесс колебаний величины q(t) (а следовательно, и величин i(t), v(t)) в простейшем электрическом контуре. В системе «емкость-индуктивность» колебания происходят так же, как и в системе «шарик-пружина».

Мат.Анализ

9. Необходимое и достаточное условие интегрируемости функций. Классы интегрируемых функций.

Th: Для того, чтобы ограниченная на сегменте [a,b] функция f(x) была интегрируемой на этом сегменте, необходимо и достаточно, чтобы для 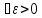нашлось такое разбиение Т сегмента [a,b], для которого

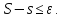
Доказательство: 1)необходимость. Пусть ф-я f(x) интегрируема на сегменте [a,b]. Обозначим через I – предел интегрируемых сумм этой функции. По определению предела интегрируемых сумм для 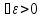можно указать такое 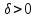, что для разбиения Т, удовлетворяющего условию , независимо от выбора точек 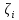на частичных сегментах разбиения выполняется нер-во

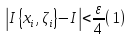
Зафиксируем одно такое разбиение Т. Для данного разбиения Т можно указать такие 2 интегр. суммы, что

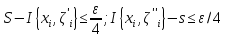
Отметим, что обе интегр. суммы 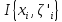и удовлетворяют неравенству (1). Из соотношения

нер-ва (1) и неравенств

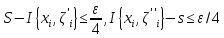
вытекает

2) Достаточность . Т.К. Для т справедливы неравенства , согласно условию теоремы, можно указать такое разбиение, что . В силу произвольности .

Общее значение чисел обозначим через I. Докажем, что I – предел интегрируемых сумм функции f(x). Действительно, в силу леммы Дарбу это число I есть общий предел при 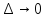верхних и нижних сумм. Поэтому для можно указать такое 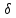, что при 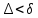выполняются неравенства 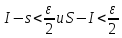, т.е. при 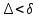, 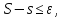причем 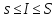. интегр. сумма 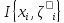данного разбиения Т заключена между 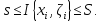Таким образом при 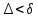величины I 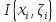и заключены между числами S b s. ⇒при

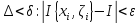
⇒ I – предел интегральных сумм. ⇒ теорема доказана.

Классы интегрируемых функций

Любая функция, ограниченная и непрерывная в некотором промежутке, является интегрируемой на этом промежутке. К классу интегрируемых функций относятся также функции, ограниченные на промежутке интегрирования и имеющие на этом промежутке конечное число точек разрыва первого рода.

Если функция f(x) интегрируема на промежутке [a,b], то и функция c f(x), где c – константа, интегрируема на этом промежутке.

Если функция f(x) интегрируема на промежутке [a,b], то и функция | f(x) | интегрируема на этом промежутке.

Если функции f(x) и g(x) интегрируемы на промежутке [a,b], то и их сумма, разность и произведение интегрируемы на этом промежутке.

Если функция f(x) интегрируема на промежутке [a,b], то она интегрируема и в любой части этого промежутка.

Если функция f(x) интегрируема в каждой части некоторого промежутка, то она интегрируема и на всем промежутке.

Если значения интегрируемой функции изменить в конечном числе точек на конечные величины, то интегрируемость функции не нарушится.

Применительно к функции f(x) , которая не определена в конечном числе точек промежутка [a,b], это означает, что ни существование интеграла , ни его величина не зависят от значений, приписанных функции f(x) в точках ее разрыва.