
- •10. Применение фундаментальных законов природы (второй закон Ньютона) к построению модели колебаний системы «шарик – пружина»
- •11. Второй способ моделирования колебаний механической системы «шарик – пружина» используя закон сохранения энергии.
- •12. Третий способ построения модели колебаний механической системы «шарик – пружина» с помощью вариационного метода.
- •13. Моделирование колебаний электрического контура. Аналогия моделей
- •9. Необходимое и достаточное условие интегрируемости функций. Классы интегрируемых функций.
- •2) Достаточность . Т.К. Для т справедливы неравенства , согласно условию теоремы, можно указать такое разбиение, что . В силу произвольности .
- •10. Теорема о среднем значении определенного интеграла
- •12. Функции нескольких переменных. Предел функции многих переменных.
- •Функция деструктора
- •Конструкторы производного класса
- •Виртуальные, дружественные, статические функции. Указатель this.
- •Решения методом Фурье краевой задачи неоднородного уравнения
- •Уравнения теплопроводности. Задача Коши. Формула Пуассона
- •Дифференциальные уравнения
Введение в математическое моделирование
10. Применение фундаментальных законов природы (второй закон Ньютона) к построению модели колебаний системы «шарик – пружина»
Пусть r – координата
шарика вдоль оси пружины, лежащей на
горизонтальной плоскости , и направления
движения шарика совпадает с ее осью.
Тогда по второму закону динамики 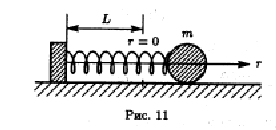
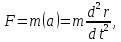
где m-масса шарика, а –его ускорение. Будем считать плоскость идеально гладкой, пренебрежем также сопротивлением воздуха и примем во внимание то, что вес шарика уравновешивается с реакцией плоскости. Единственная сила, действующая на шарик в направлении оси r, очевидно сила упругости пружины. Определим ее, используя закон Гука, гласящий, что для растяжения (сжатия) пружины необходимо приложить силу

где k>0 характеризует упругие свойства пружины, а r-величину ее растяжения или сжатия относительно нейтрального, ненагруженного положения r=0. Уравнение движения шарика принимает вид
 (1)
(1)
Оно описывает его гармонические колебания и имеет общее решение
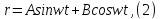
где
 – собственная частота колебаний системы
«шарик-пружина». Значения А и В определяются
из начального состояния объекта, через
величины
– собственная частота колебаний системы
«шарик-пружина». Значения А и В определяются
из начального состояния объекта, через
величины
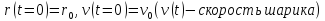 ,
причем r(t)=0
при
,
причем r(t)=0
при
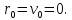
Подходы, с помощью которых строилась рассматриваемая модель не должны противоречить другим фундаментальным законам природы.
11. Второй способ моделирования колебаний механической системы «шарик – пружина» используя закон сохранения энергии.
Выведем модель «шарик-пружина» с
использованием закона сохранения
энергии. Поскольку точка крепления
пружины неподвижна , то стенка не
совершает работу над системой «пружина
– шарик» , и ее полная механическая
энергия Е остается постоянной. Вычислим
ее. Кинетическая энергия определяется
движением шарика ( пружина считается
невесомой):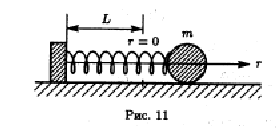

Потенциальная энергия системы «содержится» в пружине, ее нетрудно найти, определив работу, необходимую для растяжения (сжатия) пружины на величину r:

Для неизменной со временем величины
 (интеграла энергии) получаем
(интеграла энергии) получаем
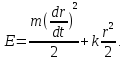
Так как
 ,
то продифференцировав интеграл энергии
по t, приходим к выражению
,
то продифференцировав интеграл энергии
по t, приходим к выражению
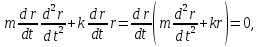
т.е. к уравнению
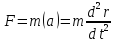 ,
проверив тем самым правильность его
получения.
,
проверив тем самым правильность его
получения.
12. Третий способ построения модели колебаний механической системы «шарик – пружина» с помощью вариационного метода.
Воспользуемся принципом Гамильтона
для построения движения шарика,
соединенного с пружиной. В качестве
обобщенной координаты естественно
выбрать обычную эйлерову координату
шарика r(t).
Тогда обобщенная скорость
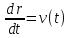 – обычная скорость шарика. Функция
Лагранжа
– обычная скорость шарика. Функция
Лагранжа
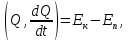
равная
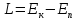 , записывается через значения кинетической
и потенциальной энергии системы:
, записывается через значения кинетической
и потенциальной энергии системы:
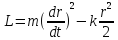
Для величины действия получаем выражение
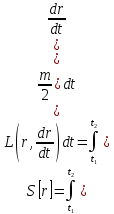
Теперь вычислим действие в вариациях
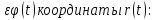
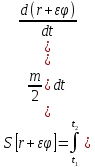
Последнюю формулу необходимо
продифференцировать по
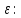

и положить в ней

Правая часть выражения с помощью
интегрирования ее первого члена по
частям и с учетом того, что
 в моменты
в моменты
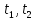 ,
преобразуется к виду
,
преобразуется к виду

Поскольку пробная функция
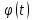 ,
фигурирующая в формулировке принципа
наименьшего действия, произвольна, то
часть выражения, стоящая под знаком
интеграла в квадратных скобках, должна
быть равна нулю во все моменты времени
,
фигурирующая в формулировке принципа
наименьшего действия, произвольна, то
часть выражения, стоящая под знаком
интеграла в квадратных скобках, должна
быть равна нулю во все моменты времени
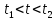 :
:
 т.е.
движение системы должно описываться
уравнением
т.е.
движение системы должно описываться
уравнением
 полученным
из закона Ньютона (первый способ) и
закона сохранения энергии (второй
способ). Все три подхода являются
эквивалентными.
полученным
из закона Ньютона (первый способ) и
закона сохранения энергии (второй
способ). Все три подхода являются
эквивалентными.
