
5) Үш еселі интеграл
1. Үш еселі интеграл анықтамасы.
2. Қасиеттері (біреуі дәлелдеуімен).
3. Үш еселі интегралды қайталама жай интегралға келтіру.
Кеңістіктегі
кубтелетін V аймағында
 үзіліссіз функциясы берілсін. V аймағын
көлемдері
үзіліссіз функциясы берілсін. V аймағын
көлемдері болатын n бөліктерге бөлшектейміз. V
аймағы және элементар
болатын n бөліктерге бөлшектейміз. V
аймағы және элементар облыстардың көлемдері де солай белгіленеді
деп ұйғарайық. Әрбір бөлік
облыстардың көлемдері де солай белгіленеді
деп ұйғарайық. Әрбір бөлік бойынан қалауымызша кез келген
бойынан қалауымызша кез келген нүктесін алып, бұл нүктедегі берілген
нүктесін алып, бұл нүктедегі берілген функциясының
функциясының мәнін
мәнін көлеміне көбейтеміз де, қосынды
көлеміне көбейтеміз де, қосынды
 (8.9)
(8.9)
құрастырып,
оны интегралдық қосынды деп атаймыз.
 бөліктің диаметрін
бөліктің диаметрін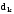 ,
ал диаметрлерінің ең үлкенін
,
ал диаметрлерінің ең үлкенін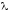 деп белгілеп,
деп белгілеп, интегралдық қосындысының шегін
қарастырайық.
интегралдық қосындысының шегін
қарастырайық.
Анықтама
Егер
 ұмтылғанда (8.9) интегралдық қосындының
шегі бар болып және ол шек V аймағын
ұмтылғанда (8.9) интегралдық қосындының
шегі бар болып және ол шек V аймағын бөліктерге бөлшектеу тәсілінен де,
олардың әрбіреуінен
бөліктерге бөлшектеу тәсілінен де,
олардың әрбіреуінен нүктесін қалап алу әдісінен де тәуелсіз
болса, онда бұл шек
нүктесін қалап алу әдісінен де тәуелсіз
болса, онда бұл шек функциясының V аймағы бойынша алынған
үш еселі интеграл деп аталады да, былай
белгіленеді:
функциясының V аймағы бойынша алынған
үш еселі интеграл деп аталады да, былай
белгіленеді:

Теорема
1)
Тұйық, шенелген, кубтелетін V аймағында
үзіліссіз әрбір
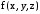 функция осы V аймағы бойынша интегралданады.
2) Тұйық, шенелген, кубтелетін V
аймағындағы көлемі нөлге тең қандайда
болмасын бір жиынның нүктелерінен тыс
жерде үзіліссіз
функция осы V аймағы бойынша интегралданады.
2) Тұйық, шенелген, кубтелетін V
аймағындағы көлемі нөлге тең қандайда
болмасын бір жиынның нүктелерінен тыс
жерде үзіліссіз функция осы аймақ бойынша интегралданады.
функция осы аймақ бойынша интегралданады.
Үш еселі интегралдың негізгі қасиеттері:
1)
Егер с – тұрақты, ал
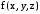 функциясы V аймағында интегралданса,
онда
функциясы V аймағында интегралданса,
онда көбейтіндісі де интегралданады және
мына теңдік орындалады
көбейтіндісі де интегралданады және
мына теңдік орындалады

2)
Егер V аймағында
 функцияларының әрқайсысы интегралданса,
олардың алгебралық қосындысы да V
аймағында интегралданады және мына
теңдік орындалады:
функцияларының әрқайсысы интегралданса,
олардың алгебралық қосындысы да V
аймағында интегралданады және мына
теңдік орындалады:


3)
Егер V
аймағында
интегралданатын функция
 болса,
онда
болса,
онда
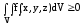
болады.
4)
Егер функция
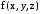 ортақ ішкі нүктелері жоқ V1
және V2
аймақтарында интегралданса, онда осы
аймақтардың біріктірмесі болатын V
аймағында да интегралданады және мына
теңдік орындалады.
ортақ ішкі нүктелері жоқ V1
және V2
аймақтарында интегралданса, онда осы
аймақтардың біріктірмесі болатын V
аймағында да интегралданады және мына
теңдік орындалады.
 .
.
5)
V аймағында
 пен
пен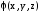 функцияларының әрқайсысы интегралданатын
болып және олардың арасында
функцияларының әрқайсысы интегралданатын
болып және олардың арасында теңсіздігі орындалса, онда
теңсіздігі орындалса, онда
 .
.
6)
Егер
 функциясының абсолют шамасы
функциясының абсолют шамасы V аймағында интегралданса, онда функцияның
өзіде осы аймақта интегралданады және
V аймағында интегралданса, онда функцияның
өзіде осы аймақта интегралданады және

теңсіздігі орындалады.
7)
V аймағында интегралданатын
 функциясы осы аймақта
функциясы осы аймақта теңсіздігін қанағаттандырса, онда
теңсіздігін қанағаттандырса, онда

теңсіздігі орындалады.
Үш еселі интегралды қайталама жай интегралға келтіру


6) Үш еселі интегралда айнымалыларды алмастыру
1. Үш еселі интегралда цилидрлік координаттарға көшу (формуласын жазу).
2. Үш еселі интегралда сфералық координаттарға көшу (қорытуымен).
Декарттық
координаттар жүйесінде
 нүктесі беріліп, оның Оху жазықтығындағы
проекциясы М1
нүктесі болсын. М нүктесі оның аппликатасы
z және М1
өзінің полярлық кординаттары
нүктесі беріліп, оның Оху жазықтығындағы
проекциясы М1
нүктесі болсын. М нүктесі оның аппликатасы
z және М1
өзінің полярлық кординаттары
 мен
мен арқылы анықталса, онда
арқылы анықталса, онда шамалары М нүктесінің цилиндрлік
координаттары болады. М нүктесінің
декарттық және цилиндрлік координаттарының
арасындағы байланыс мына формулалармен
анықталады (10-сурет):
шамалары М нүктесінің цилиндрлік
координаттары болады. М нүктесінің
декарттық және цилиндрлік координаттарының
арасындағы байланыс мына формулалармен
анықталады (10-сурет):

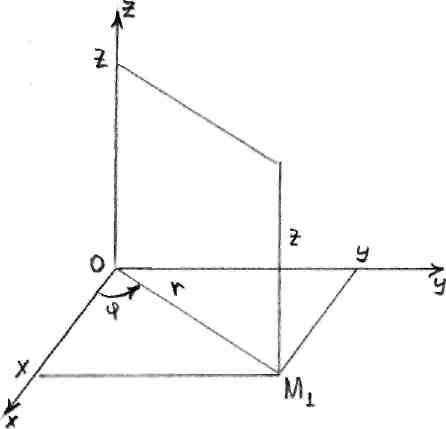
10-сурет
 координаттарын
координаттарын
 координаталарымен ауыстыру якобианы:
координаталарымен ауыстыру якобианы:

болады. Сондықтан үш еселі интегралда айнымалыларды ауыстыру мына формула арқылы орындалады:
 .
.
Үш еселі интегралда сфералық координаттарға көшу
(қорытуымен)
Оxyz кеңістігінде М нүктесінің орнын:
а)
О нүктесінен М нүктесіне дейінгі қашықтық
 ;
;
б)
ОМ кесіндісі мен Оz өсінің оң бағыты
арасындағы бұрыш
 ;
;
в)
ОМ кесіндінің Оху жазықтығындағы
проекциясы ОМ1
мен Ох өсінің оң бағыты арасындағы бұрыш
 арқылы анықтасақ, онда осы
арқылы анықтасақ, онда осы шамалары М нүктесінің сфералық
координаттары болады.М
нүктесінің декарттық және сфералық
координаттар арасындағы
шамалары М нүктесінің сфералық
координаттары болады.М
нүктесінің декарттық және сфералық
координаттар арасындағы
