
- •1.Пікірлер есептеуіндегі резолюция әдісі.
- •3.Предикаттар логикасының тілі.
- •10.Предикаттар логикасындағы резолюция әдісі.
- •13.Жиында қорыту және салдар ұғымдары.
- •14.A импликация a формуласының теорема болатыны туралы лемма.
- •15. Дедукция теоремасы. Дедукция теоремасының салдарлары.
- •16. Предикаттар логикасының тілі.
- •17. Бос және байланған айнымалылар.
- •18.Термнің мәні және формуланың структурада орындалуы.
- •19.Орындалатын формулалардың қасиеттері
- •21.Ішкі структура.
- •22.Пренексті нормаланған форма туралы теорема.
- •25.Моделдегі анықталымдылық.
- •27) Тъюринг машиналары.
- •30. Қорыту.
21.Ішкі структура.
а)Ішкі структура ұғымы. Анықтама және мысалдар.
в) Ішкі структура.туралы тұжырым.
. Ішкі структура.
Аныктама.
σ сигнатурасының
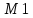 =<М1,σ>
=<М1,σ>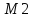 =<M2,σ>
структуралары
берілсін.
=<M2,σ>
структуралары
берілсін.
М1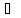 М2
және
М, М2
жиындарында σ сигнатурасының
символдарының
интерпретациялары бірдей
анықталса,
М2
және
М, М2
жиындарында σ сигнатурасының
символдарының
интерпретациялары бірдей
анықталса,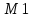 структурасын
структурасын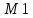 структурасының
iшкі
структурасы
деп атаймыз. Ал
структурасының
iшкі
структурасы
деп атаймыз. Ал
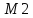 структурасы
структурасы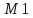 структурасынқамтушы
структура
делінеді.
структурасынқамтушы
структура
делінеді.
Келесі тұжырым кванторсыз формулалардың iшкi структураларға қарағанда өз мағынасын «өзгертпейтінін» көрсетеді
Келісім.
L
тілінің
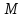 =<
М,... >
структурасы берілсін.
Егер f,R,
с
- L
тілінің
функционалдық,
предикаттық
жэне константалық
символдары болсын. Онда fм,Rм
және
см
арқылы
осы символ- дардың
=<
М,... >
структурасы берілсін.
Егер f,R,
с
- L
тілінің
функционалдық,
предикаттық
жэне константалық
символдары болсын. Онда fм,Rм
және
см
арқылы
осы символ- дардың
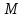 структурасындағы
сәйкес
интерпретацияларын
структурасындағы
сәйкес
интерпретацияларын
белгілейміз.
Егер t(x)
терм
және
b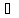 Мп
болса, онда tM(b)
аркылы
берілген
термнің
Мп
болса, онда tM(b)
аркылы
берілген
термнің
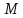 структурасындағы
b
структурасындағы
b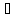 Мп
тізбегіндегі
мәні
белгіленеді.
Мп
тізбегіндегі
мәні
белгіленеді.
а)Ішкі структура ұғымы. Анықтама және мысалдар.
Тұжырым
5.8 L
тілінің
стуктурасы
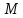 =<М,...
> - N
=<N,...>
структурасының
iшкi
структурасы,
ал φ(х)
осы
тілдің
кванторсыз формуласы
болсын. Онда кез келген а
=<М,...
> - N
=<N,...>
структурасының
iшкi
структурасы,
ал φ(х)
осы
тілдің
кванторсыз формуласы
болсын. Онда кез келген а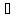 Мт
үшін
М|=
φ(а)
Мт
үшін
М|=
φ(а)
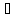
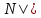 (a)
(a)
Дэлелдеуі.
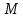 -
-
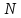 структурасының
ішкі
структурасы болғандықтан,
сигнатуралық
символдар оларда бірдей
интерпретацияланады. Сондықтан
бұл
структуралардағы
сигнатуралық
символдарды бірдей
белгімен
таңбалаймыз.
Енді
теореманы
термдер мен формулалардың
күрделілігі
бойынша дәлелдейік.
структурасының
ішкі
структурасы болғандықтан,
сигнатуралық
символдар оларда бірдей
интерпретацияланады. Сондықтан
бұл
структуралардағы
сигнатуралық
символдарды бірдей
белгімен
таңбалаймыз.
Енді
теореманы
термдер мен формулалардың
күрделілігі
бойынша дәлелдейік.
Алдымен
егер t(x)
терм және
b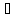 Мп
болса, онда
Мп
болса, онда
tM(b)=tN{b) (*)
теңдігі орындалатынын керсетейік
Егер t(x) := с константалық терм болса, онда см = сN .
Егер t(x) := xi айнымалы термі болса, онда tM(b) = хi = tN(b). Енді t(x):=f(t1,t2,…tn) функционалдық терм болса, онда
tM(b) = tN (b) болатынын дәлелдейік.
tМ(b) = tМ (t1М ,t2M(b),…, tnM(b))=fn (t1M(b),t2M(b),..., tnM(b))b=
= fN(t1N(b), t2N(b), ..., tnN(b)) =f N(b). Демек термдер үшін (*) тұжырымы дәлелденді.
Енді
тұжырымды формулалар үшін
дәлелдейік.
φ t1(x)
=
t2(x)
болса,
t1(x)
=
t2(x)
болса,
онда
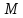 =φ(b)
=φ(b)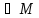 |=tM(b)
=
tM{b)
|=tM(b)
=
tM{b)
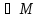 tN(b)
= tN(b)
tN(b)
= tN(b)
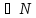 |=
φ(b)
|=
φ(b)
Егер
φ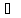 R(t1,t2,...,tm)
түріндегі
формула болса, онда
R(t1,t2,...,tm)
түріндегі
формула болса, онда
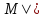 j(b)
j(b)
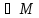 |=
RM(t1M(b),t2M(b),..,tmM(b))
|=
RM(t1M(b),t2M(b),..,tmM(b))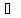
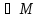 |=
RN(t1M(b),t2M(b),..,tmM(b)))
|=
RN(t1M(b),t2M(b),..,tmM(b))) Y
Y
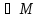 |=
RN(t1N(b),t2N(b),..,tmN(b
|=
RN(t1N(b),t2N(b),..,tmN(b
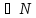 |=
RN(t1N(b),t2N(b),..,tmN(b)))
|=
RN(t1N(b),t2N(b),..,tmN(b)))
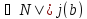
Сонымен атомдық формулалар үшін тұжырымды дәлелдейік.
Егер
φ(х)
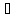 ¬ψ
(х)
туріндегі
формула болса, онда
¬ψ
(х)
туріндегі
формула болса, онда
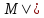 φ(b)
φ(b)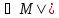 ¬ψ(b)
¬ψ(b)
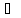
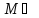 φ(b)
φ(b)
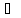
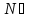 ψ(b)
ψ(b)
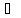
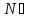 ¬ψ(b)
¬ψ(b)
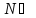 φ(b)
φ(b)
Егер
φ(х)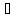 ψ(х)˄
ψ(х)˄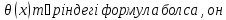 да
да
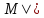 φ(b)
φ(b)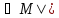 ψ(b)
˄
ψ(b)
˄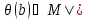 ψ(b)&
ψ(b)&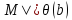
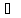
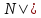 ψ(b)&
ψ(b)&
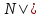 ψ(b)
˄
ψ(b)
˄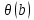
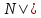 φ(b)
φ(b)
Сонымен тұжырым кванторсыз формула үшін толық дәлелденді.
Енді берілген тілдің структураларын сараптауда басты кызмет атқаратын структуралардың гомоморфизмі мен изоморфизмі ұғымдарын енгізейік.
Аныктама.
σ сигнатурасының М1=<М1,σ>
жэне M2=<M2,σ>
структуралары
6epiлiп,f:
М1
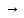 М2
олардың негізгі
жиындарының
арасындағы бейнелеуі үшін келесі:
М2
олардың негізгі
жиындарының
арасындағы бейнелеуі үшін келесі:
Егер
g
және
h
-
т
орынды алгебралық амалдары σ сигнатурасының
т
орынды функционалдық символының М1
және М2
структураларындағы
сәйкес интерпретациялары болып, кез
келген а1,...,ат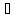 М1
элементтері үшін
М1
элементтері үшін
f(g(а1,...,ат))=h(f(а1),…,f(ат))
теңдігі орындалады,
Сәйкес
М1
және
М2
жиындарында анықталған
Р
және
S
-
п орынды
қатынастары
σ сигнатурасының
қандай
да 6ip
п
орынды R
предикаттық
символының
М1
және
М2
структураларындағы
сәйкес
интерпретациялары болса, кез келген
а1,...,ат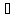 М1
элементтері үшін М1
структурасында
Р(а1,..,ап)
қатынасы
орындалады
М1
элементтері үшін М1
структурасында
Р(а1,..,ап)
қатынасы
орындалады
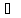 М2
структурасындаS(f(а1),…,f(аn))
қатынасы
орындалады,
М2
структурасындаS(f(а1),…,f(аn))
қатынасы
орындалады,
Егер
ак
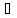 М1
жэне Ьк
М1
жэне Ьк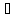 М2
элементтері
σ
сигнатурасының
ск
константа
символының
М1
жэне М2
структураларындағы
сәйкес
интерпретациялары болса, онда
f(ak)=
bk
теңдігі
орындалады.
М2
элементтері
σ
сигнатурасының
ск
константа
символының
М1
жэне М2
структураларындағы
сәйкес
интерпретациялары болса, онда
f(ak)=
bk
теңдігі
орындалады.
в) Ішкі структура.туралы тұжырым.
