
- •1 Основные разделы кибернетики.
- •2 Основоположники кибернетики
- •3 Категория управления
- •4 Определение Шеннона
- •6 Дискретная (цифровая) и непрерывная (аналоговая) информация
- •7 Процесс дискретизации
- •9 Теорема Найквиста
- •10 Вероятностный подход к измерению дискретной и непрерывной информации
- •11 Информационная энтропия
- •12 Энтропия Шеннона
- •13 Измерение количества информации
- •14 Измерение количества энтропии
- •16 Источник информации
- •18 Условная энтропия
- •19 Полная энтропия Энтропия — это количество информации, приходящейся на одно элементарное сообщение источника, вырабатывающего статистически независимые сообщения. Математические свойства
- •20 Случайная средняя энтропия
19 Полная энтропия Энтропия — это количество информации, приходящейся на одно элементарное сообщение источника, вырабатывающего статистически независимые сообщения. Математические свойства
Неотрицательность:
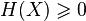 .
.Ограниченность:
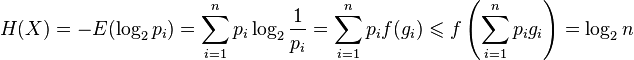 ,
что вытекает из неравенства
Йенсена для
вогнутой функции
,
что вытекает из неравенства
Йенсена для
вогнутой функции 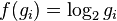 и
и 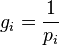 .
Если все
.
Если все 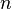 элементов
из
элементов
из 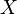 равновероятны,
равновероятны, 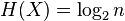 .
.Если
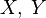 независимы,
то
независимы,
то  .
.Энтропия — выпуклая вверх функция распределения вероятностей элементов.
Если
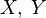 имеют
одинаковое распределение вероятностей
элементов, то
имеют
одинаковое распределение вероятностей
элементов, то  .
.
Эффективность.
Алфавит
может иметь вероятностное распределение
далекое от равномерного.
Если исходный алфавит содержит ![]() символов,
тогда его можно сравнить с «оптимизированным
алфавитом», вероятностное распределение
которого равномерное. Соотношение
энтропии исходного и оптимизированного
алфавита — это эффективность исходного
алфавита, которая может быть выражена
в процентах. Эффективность исходного
алфавита с
символов,
тогда его можно сравнить с «оптимизированным
алфавитом», вероятностное распределение
которого равномерное. Соотношение
энтропии исходного и оптимизированного
алфавита — это эффективность исходного
алфавита, которая может быть выражена
в процентах. Эффективность исходного
алфавита с ![]() символами
может быть также определена как
его
символами
может быть также определена как
его ![]() -арная
энтропия. Энтропия ограничивает
максимально возможное сжатие без потерь
(или почти без потерь), которое может
быть реализовано при использовании
теоретически —типичного
набора или,
на практике, — кодирования
Хаффмана, кодирования
Лемпеля — Зива — Велча или арифметического
кодирования.
-арная
энтропия. Энтропия ограничивает
максимально возможное сжатие без потерь
(или почти без потерь), которое может
быть реализовано при использовании
теоретически —типичного
набора или,
на практике, — кодирования
Хаффмана, кодирования
Лемпеля — Зива — Велча или арифметического
кодирования.
20 Случайная средняя энтропия
Пусть x˜ и y˜ — случайные величины с конечными носителями (не обязательно независимые). Обозначим для краткости suppy˜ через Y. Для каждого y∈Y определена случайная величина (x˜|y˜=y), принимающая произвольное значение x с вероятностью Pr(x˜=x|y˜=y). Очевидно, что носитель этой случайной величины конечен (так как он содержится в suppx˜), поэтому ее энтропия определена. Энтропия в этой статье всюду обозначается через H. Тогда (средней) условной энтропией H(x˜|y˜) случайной величины x˜ относительно y˜ называется математическое ожидание случайной величины y↦H(x˜|y˜=y) (y∈Y), взятое по распределению вероятностей случайной величины y˜ на Y. Другими словами,
H(x˜|y˜)=∑y∈YPr(y˜=y)H(x˜|y˜=y).
Говоря неформально, H(x˜|y˜) является количественной мерой неопределенности случайной величины x˜ при известном случайном значении случайной величины y˜.
Имеют место следующие важнейшие свойства условной энтропии, которые нетрудно получить непосредственно или вывести из свойств обычнойэнтропии.
H(x˜|y˜)=H(x˜,y˜)−H(y˜);
0⩽H(x˜|y˜)⩽H(x˜);
H(x˜|y˜)=0 тогда и только тогда, когда для любого y∈Y случайная величина x˜ при условии y˜=y с вероятностью 1 принимает единственное значение (вообще говоря, зависящее от y);
H(x˜|y˜)=H(x˜) тогда и только тогда, когда x˜ и y˜ независимы.
