3. Метод Якоби (метод простых итераций)

Для применения метода Якоби (и метода Зейделя) необходимо, чтобы диагональные компоненты матрицы А были больше суммы остальных компонент той же строки. Заданная система не обладает таким свойством, поэтому выполняю предварительные преобразования.

Далее номер в скобках означает номер строки. Новую первую строку получаю сложением старой первой строки с другими строками, умноженными на специально подобранные коэффициенты. Записываю это в виде формулы:

(1)’ = (1) + 0,43*(2) - 0,18*(3) – 0,96*(4)

(2)’ = (2) + 0,28*(1) – 1,73*(3) + 0,12*(4)

(3)’ = (3) – 0,27*(1) - 0,75*(2) + 0,08*(4)

(4)’ = (4) + 0,04*(1) – 6,50*(2) + 8,04*(3)

Примечание: подбор коэффицентов выполнен на листе "Анализ".

Решаются системы уравнений, цель которых - обратить внедиагональные

элементы в нуль. Коэффиценты - это округлённые результаты решения

таких систем уравнений. Конечно, это не дело.

В результате получаю систему уравнений:

Для применения метода Якоби систему уравнений нужно преобразовать к виду: X = B2 + A2*X Преобразую:  Далее делю каждую строку на множитель левого столбца, то есть на 16, 7, 3, 70 соответственно. Тогда матрица А2 имеет вид : А вектор В2: 

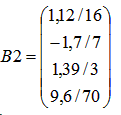
Методы оптимизации.

Поиск минимума функции одной переменной методом «тяжелого шарика».

Метод базируется на аналогии с движением тяжелого материального шарика по наклонной поверхности. Скорость шарика при движении вниз будет возрастать, и он будет стремиться занять нижнее положение, т.е. точку минимума. X_i+1 = X_i - (X_i –X_i-1) – h gradF(X_i) При  = 0 – метод превращается в обычный градиентный. При 0 <  < 1 можно получать различную эффективность метода, которая будет зависеть и от h. Вдали от оптимума поиск будет ускоряться, а вблизи возможны колебания около минимума.  - определяет память алгоритма, т.е учитывает влияние предыдущей точки, поэтому увеличение этого параметра вблизи минимума может привести к более быстрому затуханию, если градиент функции мал. Предпочтителен, когда глобальный минимум ярко выражен и локальные мелки.

Методы многомерной и условной оптимизации.

Оптимизация — в математике, информатике и исследовании операций задача нахождения экстремума (минимума или максимума) целевой функции в некоторой области конечномерного векторного пространства, ограниченной набором линейных и/или нелинейных равенств и/или неравенств.

Методы линейного программирования.

Постановка распределительной задачи.

Пусть неко­торое предприятие может изготавливать изделия четырех видов И₁ и И₂, И₃, И₄. Известно, что для изготовления изделия требуются три вида оборудования: О₁, О₂, О₃. Известно также, сколько времени потребуется на изготовление каждого изделия на каждом оборудовании, фонд времени работы оборудования (сколько времени может проработать каждое оборудование) и какая прибыль может быть получена при реализации каждого изделия (табл. 2.11). Таблица 2.11 Необходимо так распределить изделия по оборудованиям, чтобы предприятие имело максимальную прибыль. Исходные данные расчета сведены в табл. 2.11. Обозначим: b_i — ресурсы оборудования O_r, а_ij — время изготовления i-го изделия И_i на j-м оборудовании; с_j — прибыль от одного изделия И_j; х_j — количество изделий, которое необходимо выпустить на предприятии.