Раздел VIII Интегральное исчисление функции одной переменной

1. Знать определение первообразной и неопределенного интеграла .

2. Знать определение определенного интеграла и его геометрический смысл.

3. Знать таблицу основных неопределенных интегралов.

4. Для неопределенного и определенного интегралов знать правило замены переменных и формулы интегрирования по частям.

5. Знать формулу Ньютона-Лейбница.

6. Найти интегралы:

1)2)3)4)5)6)7)8)

9)10)11)12)

13)14)15)

16)17)18)

19)20)21)

22) 23)24)

25)26)27)

28)29)30)

31)32)33)

34)35)36)

37)38)39)

40)41)42)

43)44)45)46)

7. Вычислить площади фигур, ограниченных линиями:

1);

2)

3);

4)

5);

6).

Раздел IX Обыкновенные дифференциальные уравнения

1. Найти общее решение дифференциального уравнения (или решить задачу Коши):

1) 2)3)

4) 5)6)7)

8)9)

10) 11)

12) (– пост. величины)

13), 14), 15)

16) 17),

18) 19)

20) 21)22)

23) 24)

25) 26)

27) 28)

-- постоянные величины;

29) 30)

31) 32)

33)34)

35)36)

37)38)

39) 40)41)

42) 43)

44) 45)

46) 47)

2. Показать, что общее решение уравнения гармонических колебаний

может быть представлено в виде

где - произвольные постоянные.

3. Найти общее решение уравнения упругих колебаний

без учета сил сопротивления при наличии периодической внешней силы

.

Использовать запись общего решения из задачи 2.

Раздел X Двойные интегралы

1. Изменить порядок интегрирования:

1)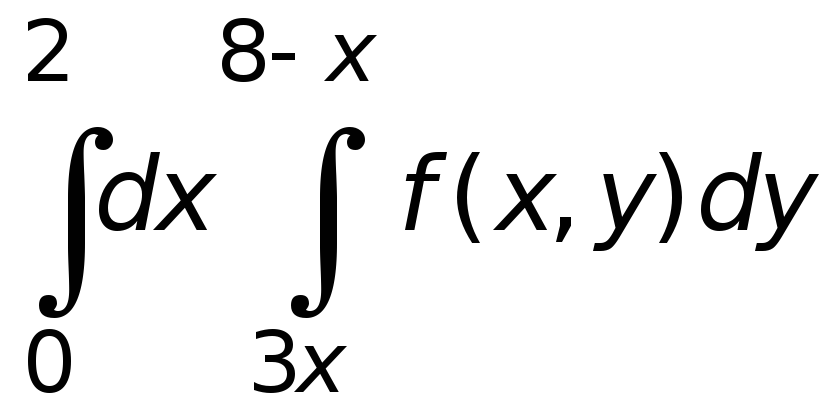, 2)

2. Перейти к полярной системе координат в интегралах:

1) 2)

3. Вычислить двойной интеграл , где областьDограничена линиями .

4. Используя двойные интегралы, вычислить:

1. площадь фигуры, ограниченной линиями

2. объем тела, ограниченного поверхностями

3) массу прямоугольной пластины со сторонамиAO=4,OB=3, поверхностная плотность которой меняется пропорционально расстоянию до стороныOAс коэффициентом пропорциональностиk=2;

4) координаты центра масс однородной пластинки, область Dкоторой ограничена линиями

Указание. Координаты центра масс находят по формулам: гдеS — площадь пластинки,

—статические моменты площади относительно осей координат.

Раздел XI Криволинейные, поверхностные интегралы и элементы теории поля

1. Знать определения скалярного и векторного полей.

2. Знать определения операторов Гамильтона и Лапласа:

Оператор Гамильтона в декартовой системе координат

Оператор Лапласа в декартовой системе координат

.

Оператор Лапласа от скалярной функции U

в декартовой системе координат

;

в цилиндрической системе координат в предположении, что

;

в сферической системе координат в предположении, что

.

3. Знать определение производной функции по направлению

и формулу для ее вычисления:

4. Знать определение градиента скалярного поля и его физический смысл

5. Знать определение дивергенции векторного поля и ее физический смысл:

6. Знать определение ротора векторного поля =

7. Уметь формулировать основные теоремы теории поля.

1) Формула Грина:

2) Формула Остроградского-Гаусса:

в векторной форме:

в координатной форме:

3) Формула Стокса:

в векторной форме:

в координатной форме:

8. Уметь доказывать следующие соотношения:

, , .

9. Вычислить криволинейные интегралы

1) по окружности,

2) по эллипсу,

3) , гдеL— отрезок прямойот точкидо точки,

4) .

10. Найти функцию U по ее полному дифференциалу

1) 2)

11. Найти производную функции в точкев направлении, составляющем равные углы с осями координат.

12. Задано векторное поле радиус-вектора . Найти где.

13. Применяя формулу Остроградского-Гаусса, преобразовать интегралы:

1)

2)

14. Применяя формулу Стокса, показать, что

, где L - любой замкнутый контур.