Федеральное агентство по образованию
Московская государственная академия тонкой химической технологии им. М.В.Ломоносова
Кафедра высшей и прикладной математики
И.А.Джемесюк, И.Р.Тишаева, С.В.Федотова
Банк математического обеспечения учебных курсов общенаучных, общеинженерных и специальных кафедр
под редакцией проф. Э.М.Карташова
учебно-методическое пособие
Москва. 2009.
УДК 51
ББК 22.1
Рецензент — доктор физ.-мат.наук,
профессор В.В. Шевелев
И.А.Джемесюк, И.Р.Тишаева, С.В.Федотова
(под ред. проф. Э.М.Карташова)
Банк математического обеспечения учебных курсов общенаучных, общеинженерных и специальных кафедр. Учебно-методическое пособие. М.: ИПЦ МИТХТ, 28 с.
Утверждено библиотечно-издательской комиссией в качестве задачника для студентов 1-го и 2-го курсов дневного отделения всех направлений и специальностей МИТХТ по дисциплине "Высшая математика", поз. /2009.
ÓМИТХТ им. М.В.Ломоносова, 2009
Работа с банком предполагает:
1. Самостоятельную проработку студентом задач Банка по мере прохождения курсов математического анализа, линейной алгебры, высшей и прикладной математики.
2. Умение решать любую задачу Банка на экзаменах и зачетах.
3. Умение четко формулировать на экзаменах и зачетах определения и теоремы, указанные в Банке.
4. Умение пользоваться Банком при изучении дисциплин общеобразовательных, общеинженерных и специальных кафедр.
5. Умение пользоваться Банком при подготовке к компьютерным и интернет-тестированиям знаний студентов по дисциплине Математика
Кафедра высшей и прикладной математики МИТХТ им. М.В. Ломоносова ставит Вас в известность, что по этому банку специальные кафедры проводят входной контроль по математике.
РАЗДЕЛ I
Элементарные функции
1. Перечислить свойства, нарисовать графики основных элементарных функций:
;
2. Построить графики следующих функций:
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
11)
12)
13)
14)
15)
16)
17)
18)
19)
20)
21)
.
3. Построить на плоскости линии, заданные уравнениями:
1)
2)
3)
4)
5)
6)
7)
8)
9)
.
4. Построить графики следующих кусочно-непрерывных функций:
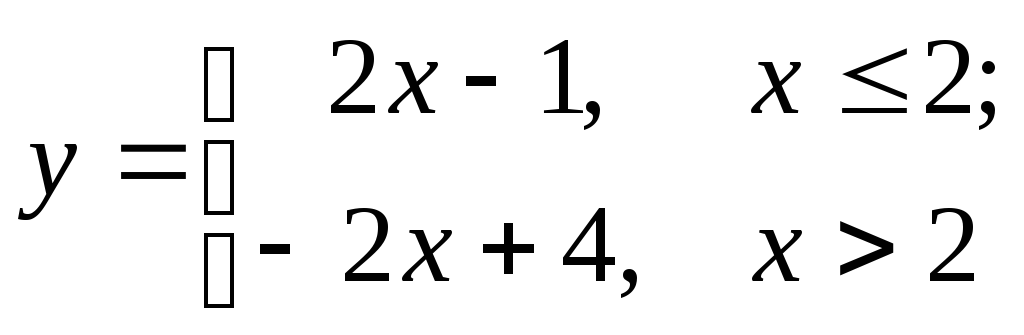2)
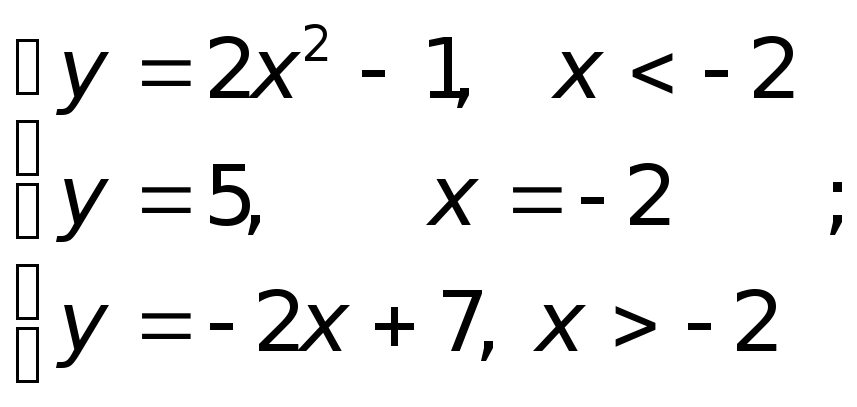
5. Выписать таблицу
значений тригонометрических функций
для основных углов a= 0;
;
;
;
;
;
.
Вычислить
;
;
;
.
6.В системе координат
построить
графики функций:
1)
2)
A >
0,k >
0.
3)
;
4)
.
Раздел II Преобразование алгебраических выражений. Уравнения и неравенства.
1. Вычислить:
1)
;
2)
; 3)
4) 
;5) 
2. Упростить:
1)
2)
3)
.
3. Разложить дробь на элементарные дроби:
1)
,
2)
4. Решить уравнения:
|
1)
|
2)
|
|
3)
|
4)
|
|
5)
|
6)
|
|
7)
|
8)
|
|
9)
|
10)
|
|
11)
|
12)
|
|
13)
|
14)
|
|
15) |
16)
|
|
17) |
18)
|
5. Решить неравенства:
1)
2)
3)
4)
5)
6)
6. Найти область определения функции:
1)
2)
3)
7. Указать множество значений функции:
1)
2)
3)
4)
5)
6)
Раздел III Пределы
1. Дать определение предела функции y=f(x) в точке (знать его геометрический смысл).
2. Дать определение бесконечно малой величины.
3. Дать определение эквивалентных бесконечно малых величин. Выписать таблицу эквивалентных бесконечно малых.
4. Вычислить пределы:
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
11)
12)
13)
14)
15)
Найти точки разрыва функции и исследовать их характер
1)
2)
3)
4)
5)
6)