
- •Скворцова м.И., Мудракова о.А.
- •Оглавление
- •Занятие 13. Функции двух переменных: основные определения. Частные производные и дифференциал функции двух переменных.
- •Задачи для самостоятельного решения
- •Занятие 14. Производные сложной и неявно заданной функции Производные сложных функций двух переменных
- •Производная неявно заданной функции
- •2) Существуют и.
- •Задачи для самостоятельного решения
- •Занятие 15. Экстремумы функции двух переменных. Элементы теории поля
- •Элементы теории поля
- •Задачи для самостоятельного решения
- •Занятие 16. Контрольная работа №3 по теме «Дифференциальное исчисление функций двух переменных». Вариант-образец.
- •Занятие 17. Метод наименьших квадратов для обработки результатов эксперимента
- •Перечень вариантов для самостоятельной работы по теме «Метод наименьших квадратов»
- •Список литературы
- •Скворцова Мария Ивановна Мудракова Ольга Александровна
Задачи для самостоятельного решения
Найти область определения функции
![]() .
.
|
|
Задана функция
![]() .
Найти:
.
Найти:
1)
![]() ;
2)
;
2)
![]() ; 3)
; 3)
![]() .
.
Найти
![]() ,
,![]() и
и![]() для функции
для функции![]() .
.
|
|
Найти
![]() ,
,![]() ,
,![]() для функции
для функции![]() :
:
1)
![]() ;
;
2)
![]() ; 3)
; 3)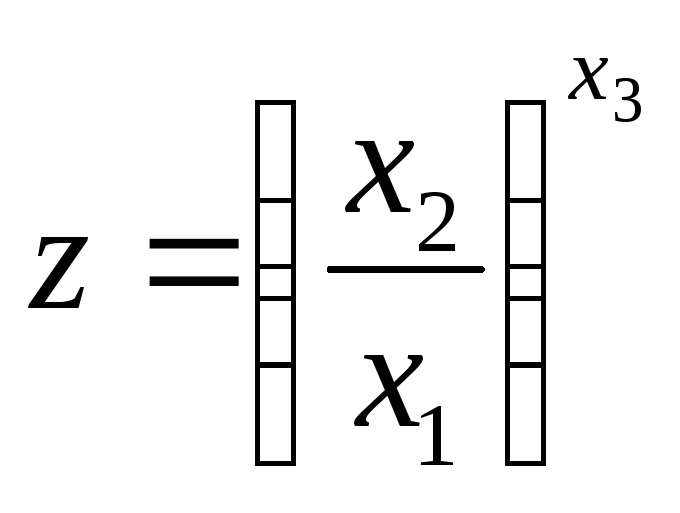 .
.
Найти
![]() ,
,![]() ,
,![]() ,
,![]() для функции
для функции![]() :
:
1)![]() ;2)
;2)![]() .
.
Занятие 14. Производные сложной и неявно заданной функции Производные сложных функций двух переменных
10. Пусть![]() ,
,![]() ,
,![]() – дифференцируемые функции. Тогда
частные производные сложной функции
– дифференцируемые функции. Тогда
частные производные сложной функции![]() вычисляются так:
вычисляются так:
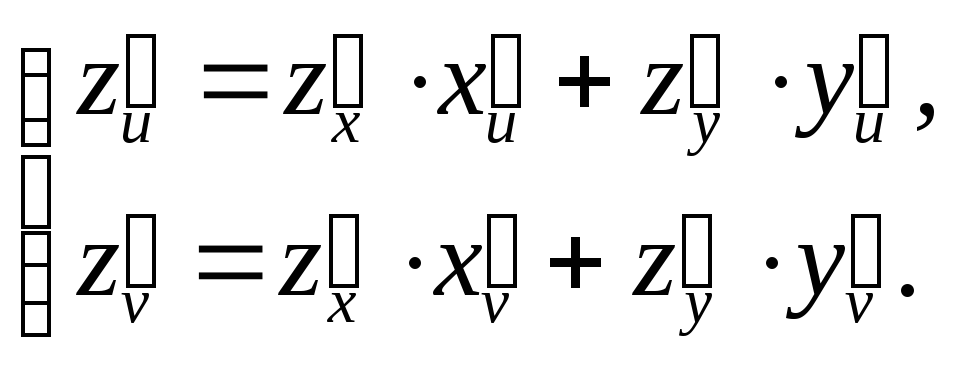 (1)
(1)
При этом в правые части формул (1) в выражения для z’x , z’yследует подставитьx=x(u,v), y=y(u,v). В результате z’x , z’y будут зависетьтолько от u и v.
Пусть
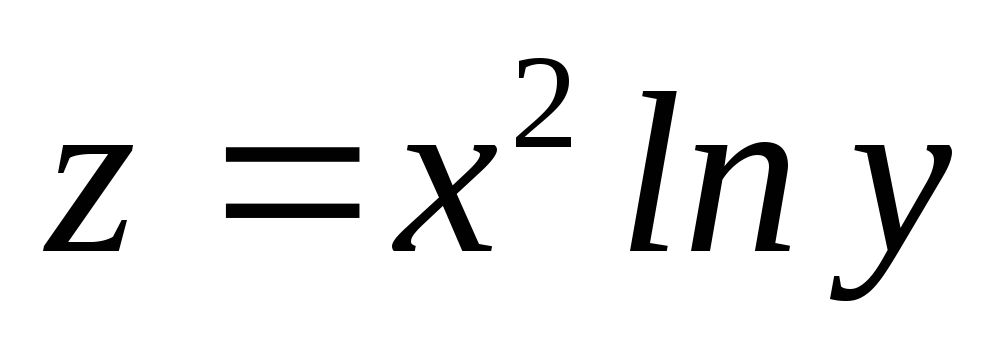 ,
,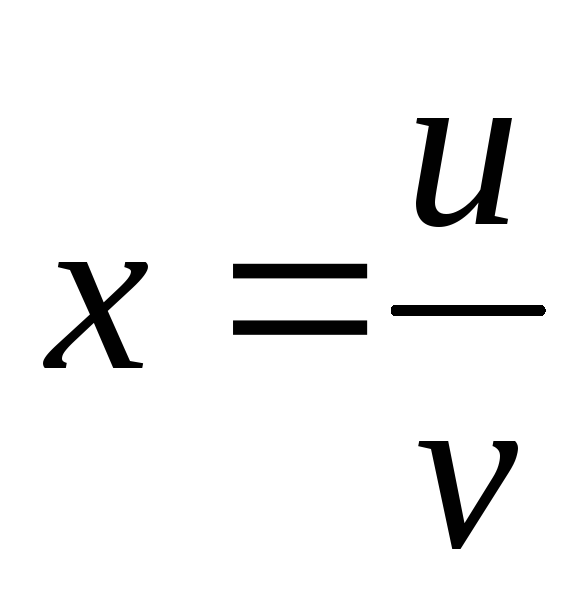 ,
,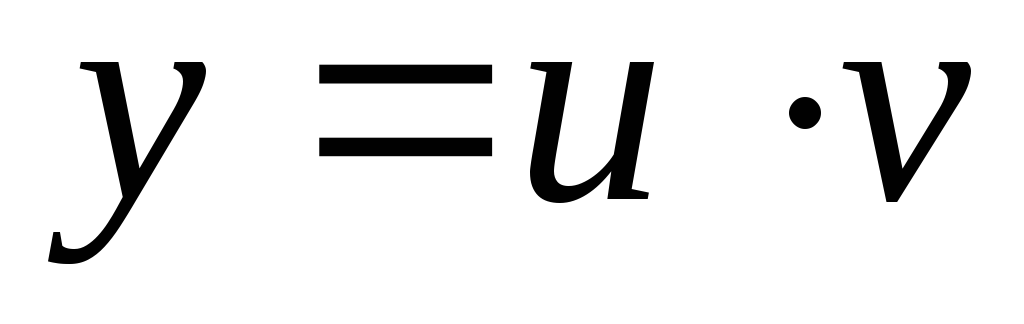 ,
т.е.
,
т.е.
![]() .
.
Найдем
![]() .
Для этого сначала найдем следующие
шесть частных производных:
.
Для этого сначала найдем следующие
шесть частных производных:
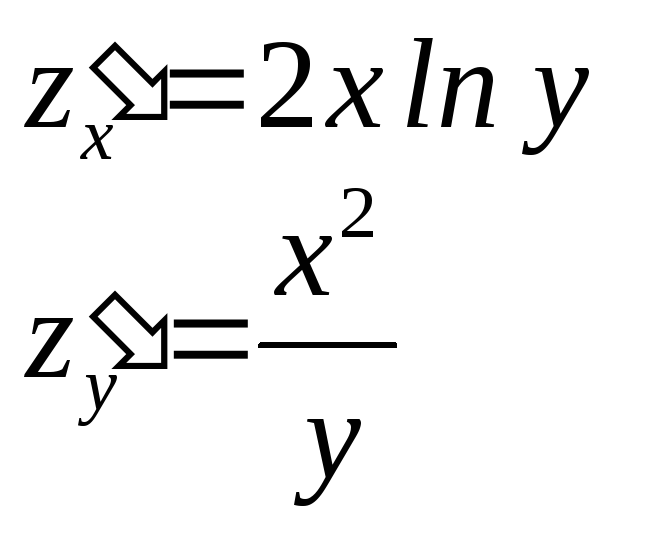
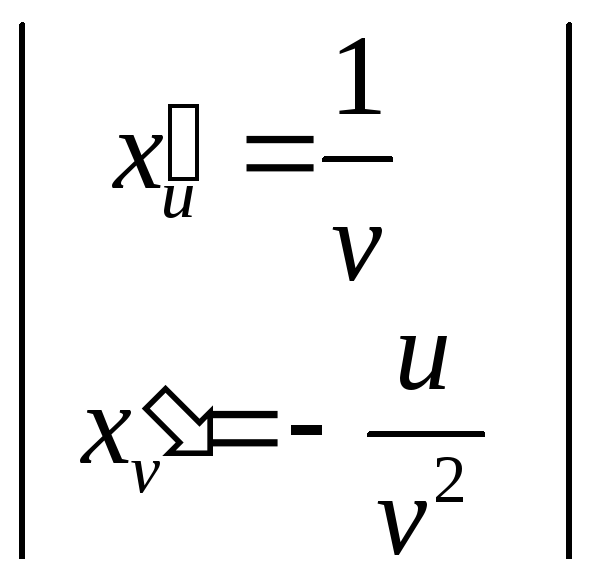
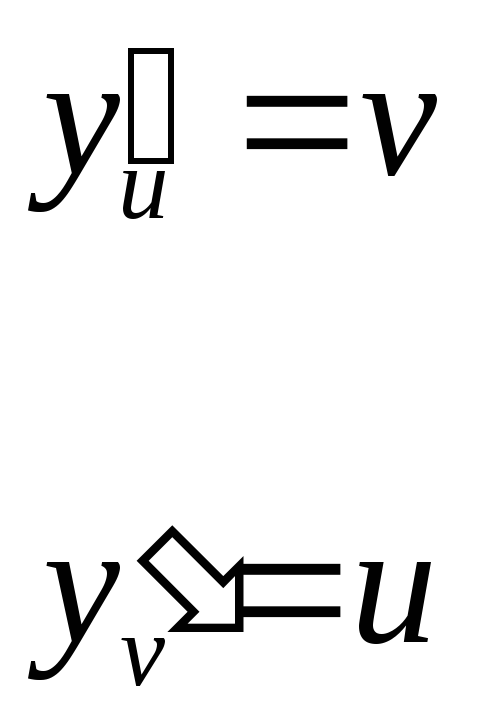
Тогда, используя формулу (1) и выражая
![]() и
и![]() через
через![]() и
и![]() ,
получим:
,
получим:
![]() ;
;
![]() .
.
20. Пусть![]() ,
,![]() ,
,![]() – дифференцируемые функции. Тогда
производная сложной функцииz(u)=z(x(u),y(u))вычисляется по формуле:
– дифференцируемые функции. Тогда
производная сложной функцииz(u)=z(x(u),y(u))вычисляется по формуле:
![]() (2)
(2)
При этом в правую часть формулы (2) в полученные выражения для z’x,z’yследует подставить x=x(u), y=y(v). В результатеdz/duбудет зависетьтолько от u .
Пусть
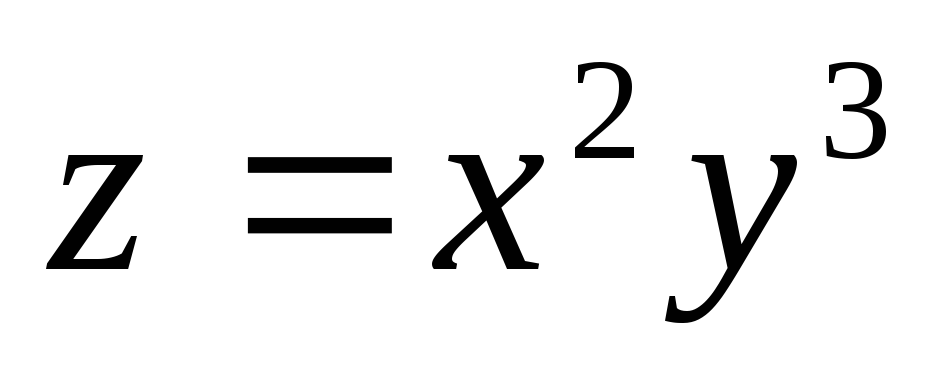 ,
,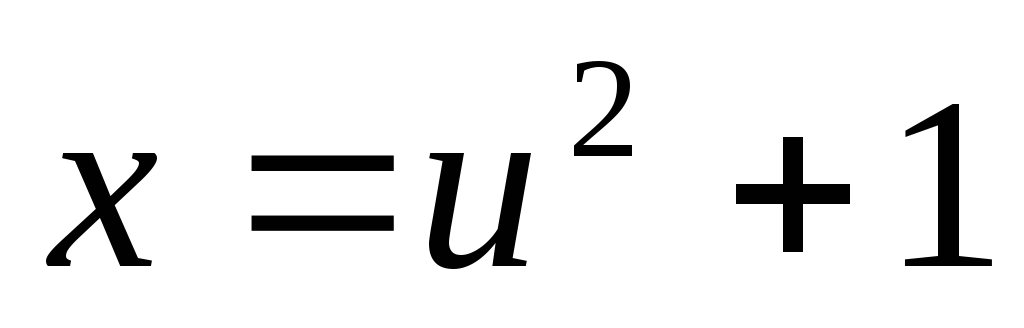 ,
,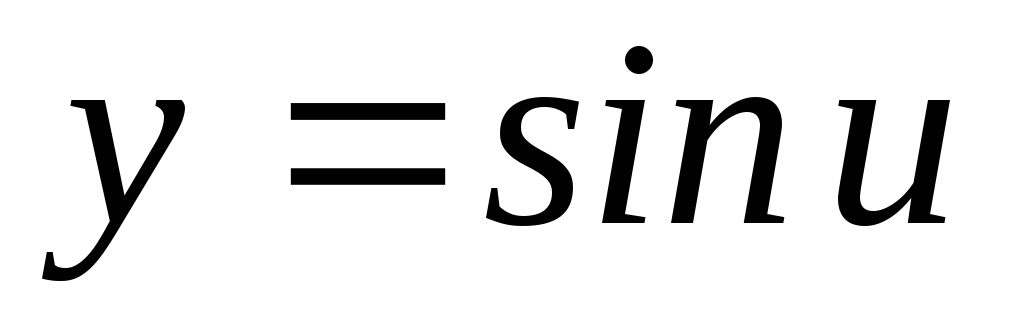 ,
т.е.
,
т.е.
![]() .
.
Найдем
![]() .
Имеем:
.
Имеем:
![]() ,
,![]() ,
,![]() ,
,![]() .
.
Используя формулу (2) и выражая
![]() и
и![]() через
через![]() и
и![]() ,
получим:
,
получим:
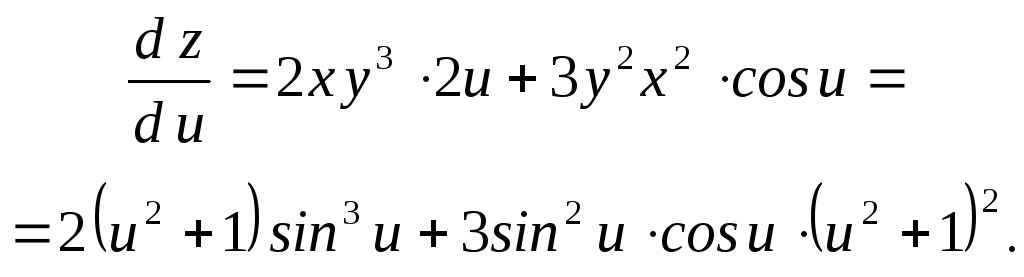
30. Пусть![]() ,
,![]() – дифференцируемые функции. Тогда
производная сложной функции
– дифференцируемые функции. Тогда
производная сложной функции![]() вычисляется по формуле:
вычисляется по формуле:
![]() (3)
(3)
При этом в правую часть формулы (3) в полученные выражения для z’x,z’yследует подставить y=y(x). В результатеz/dxбудет зависетьтолько от x .
Пусть
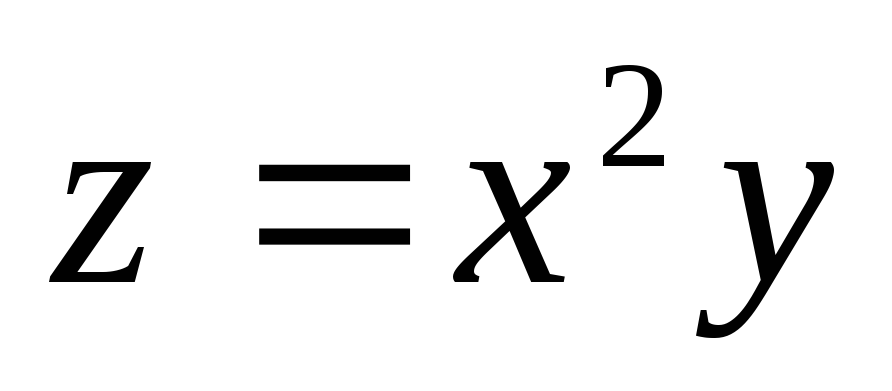 ,
,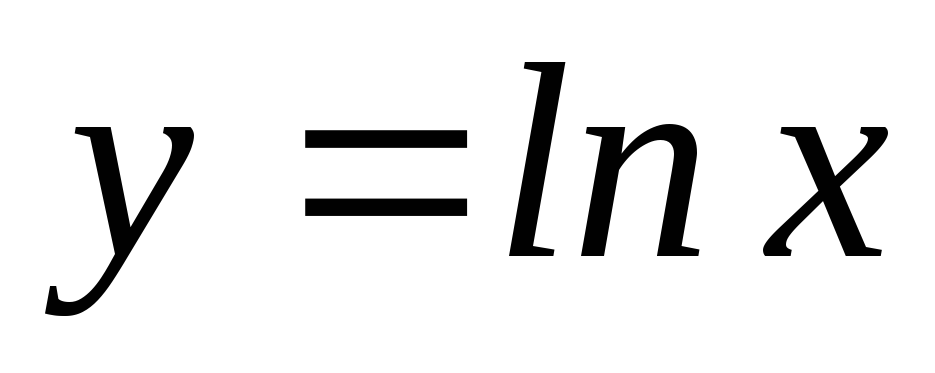 ,
т.е.
,
т.е.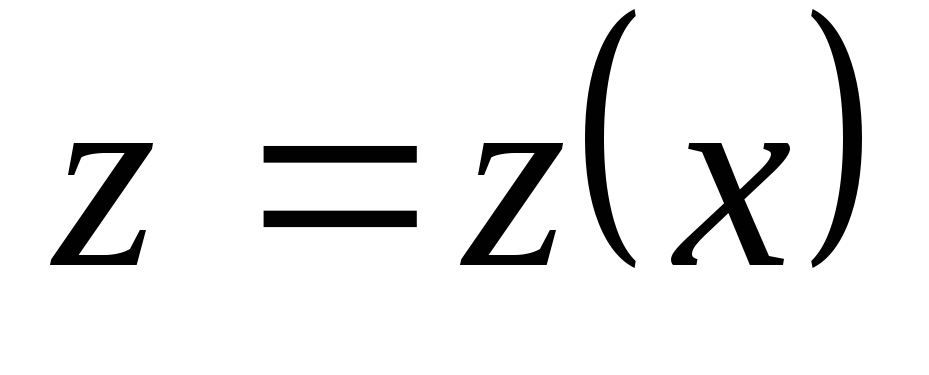 .
.
Найдем
![]() .
Имеем:
.
Имеем:
![]() ,
,![]() ,
,![]() .
.
Используя формулу (3) и выражая
![]() через
через![]() ,
получим:
,
получим:
![]() .
.
Замечания.
1) Формула (2) является частным случаем формулы (1).
2) Формула (3) является частным случаем формулы (2).
3) Формула (3) называется формулой полной производной.
4) Производные сложных функций в случаях 10-30могут быть найдены непосредственно, без использования формул (1)-(3). Однако получаемые при этом выражения могут быть слишком громоздки.
Производная неявно заданной функции
Определение. Функция
![]() называется неявно заданной, если
она задана с помощью уравнения
называется неявно заданной, если
она задана с помощью уравнения![]() ,
не разрешенного относительно «
,
не разрешенного относительно «![]() ».
».
ТЕОРЕМА.
Пусть функция
![]() задана неявно при помощи уравнения
задана неявно при помощи уравнения![]() .
Предположим, что:
.
Предположим, что:
1)
![]() ,
т.е.
,
т.е.![]() ;
;
2) Существуют и.
Тогда:
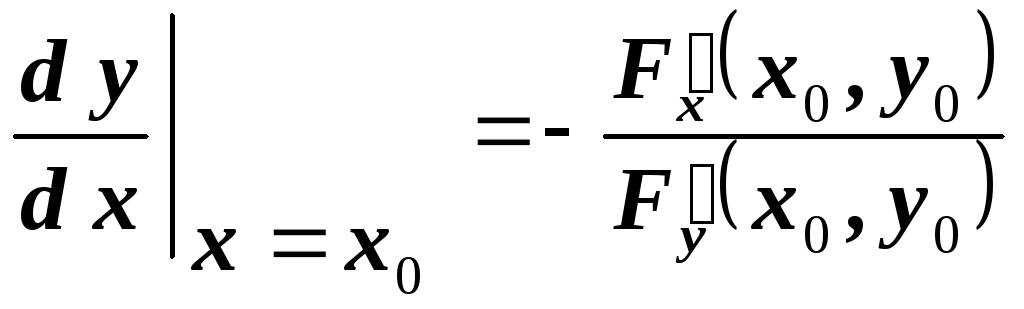 .
.
Замечание.
Рассмотрим функцию двух переменных
![]() ,
заданную неявно уравнением:
,
заданную неявно уравнением:
![]() .
.
Тогда при определенных условиях в
некоторой точке
![]() :
:
![]() ,
,![]() .
.
Рассмотрим функцию
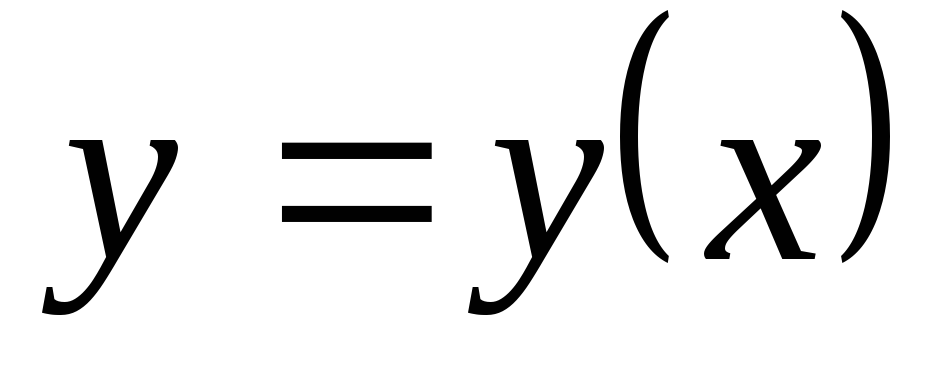 ,
заданную неявно уравнением:
,
заданную неявно уравнением: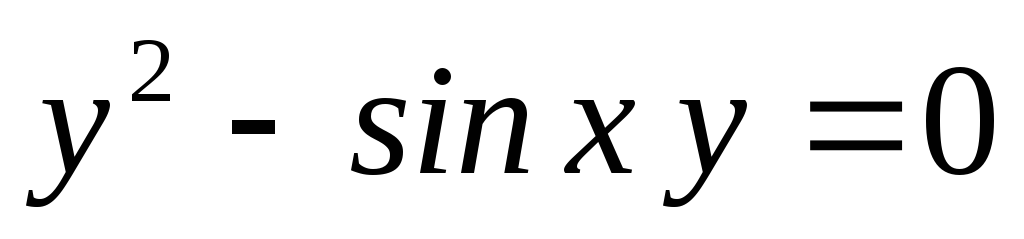 .
.
Здесь
![]() .
Найдем
.
Найдем![]() в некоторой точке
в некоторой точке![]() .
Вычислим
.
Вычислим![]() ,
,![]() :
:
![]() ,
,![]() .
.
Тогда:
![]() .
.
Рассмотрим функцию
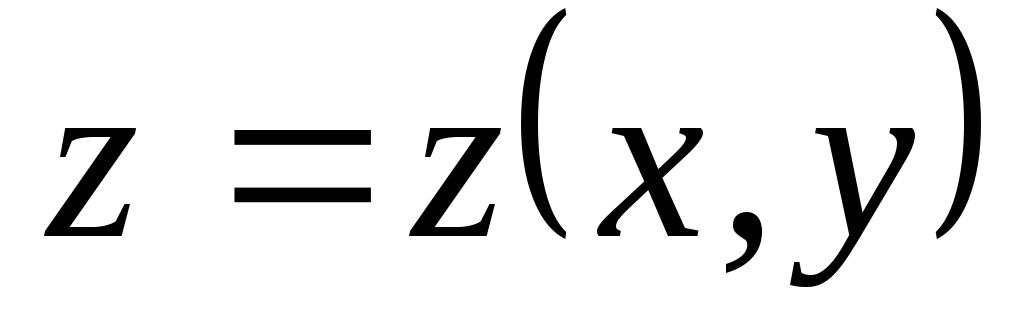 ,
заданную неявно уравнением:
,
заданную неявно уравнением: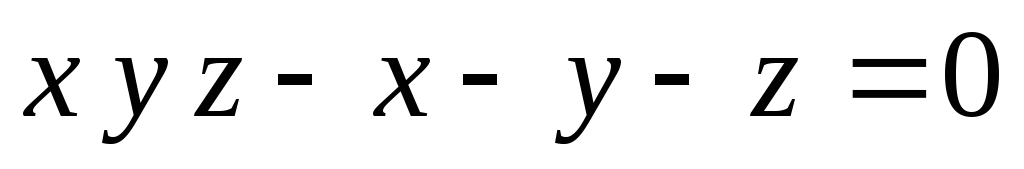 .
.
Здесь
![]() .
Найдем
.
Найдем![]() и
и![]() в некоторой точке
в некоторой точке![]() .
Вычислим
.
Вычислим![]() ,
,![]() ,
,![]() .
.
![]() ,
,![]() ,
,![]() .
.
Поэтому:
![]() ,
,![]() .
.
Задачи для самостоятельного решения
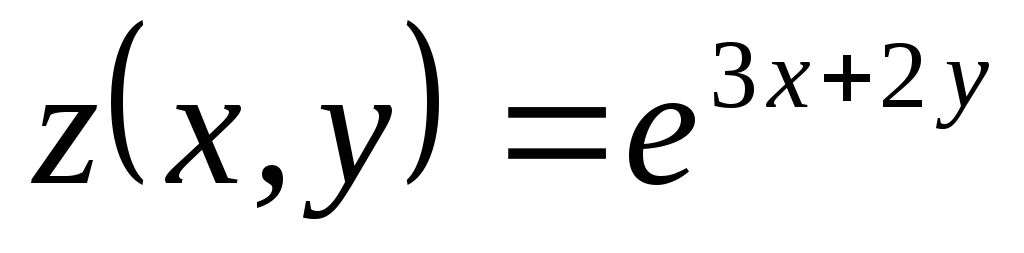 ,
,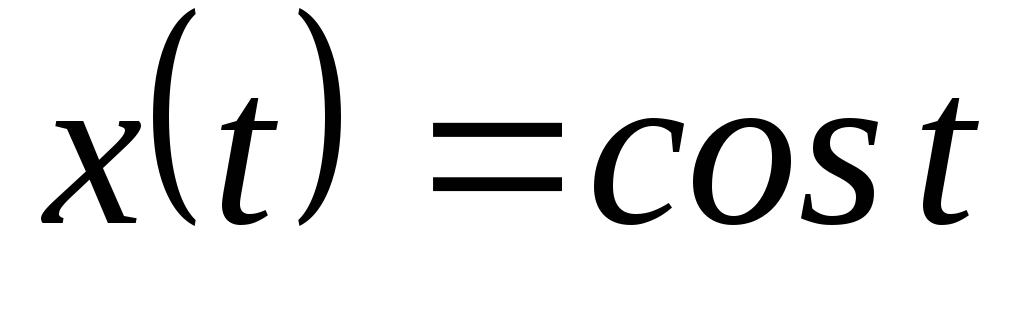 ,
,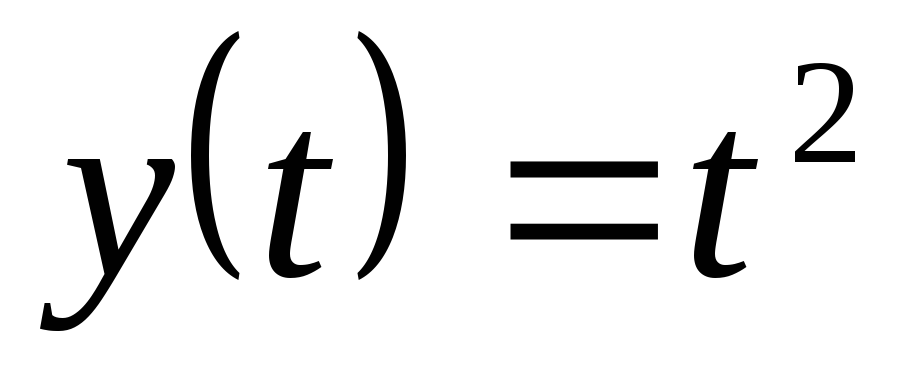 .
Найти
.
Найти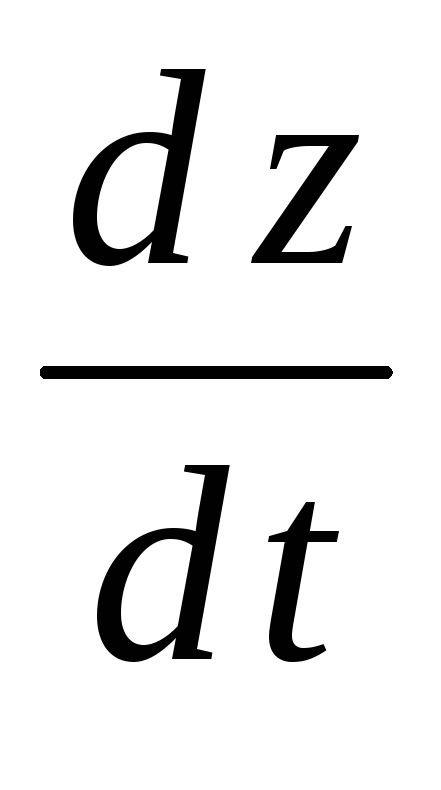 ;
;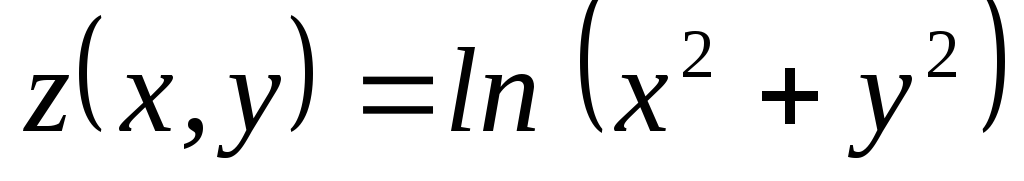 ,
,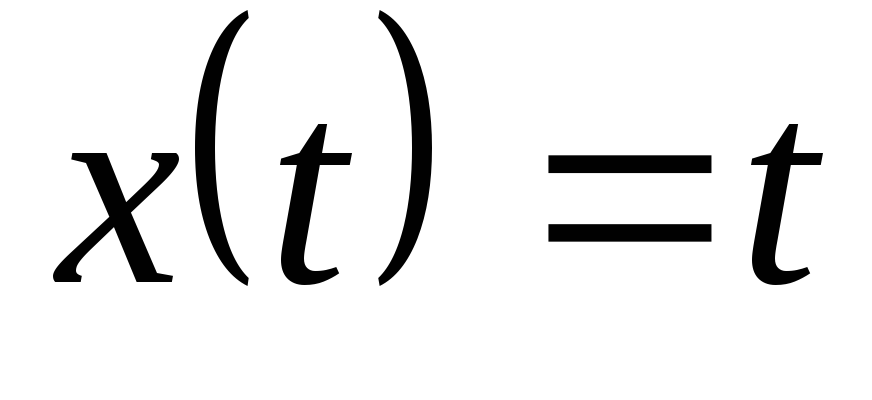 ,
,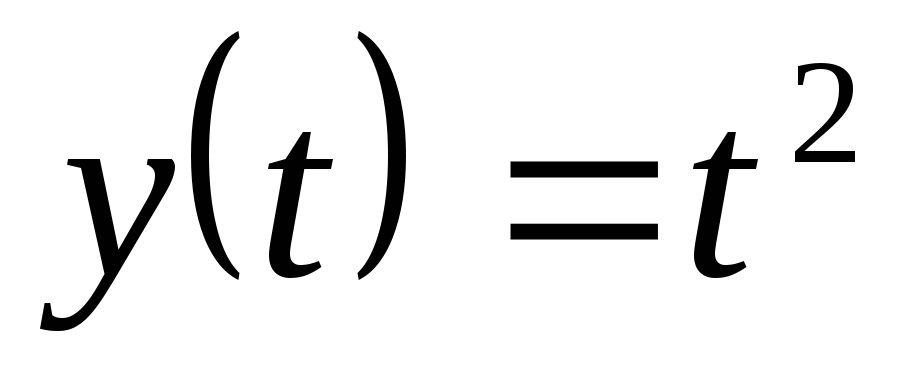 .
Найти
.
Найти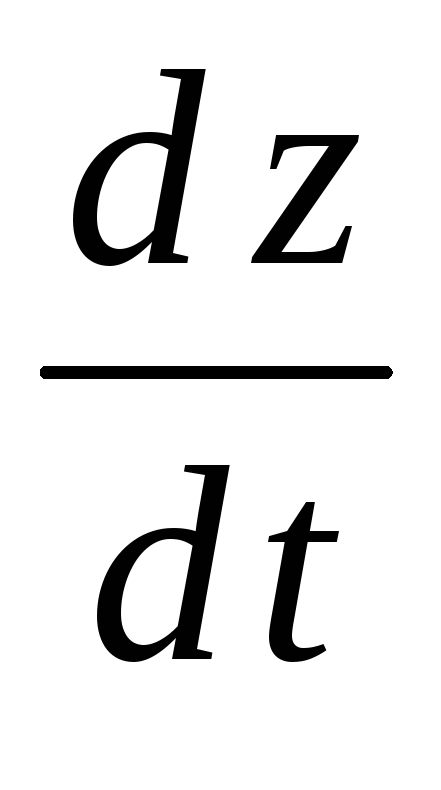 ;
;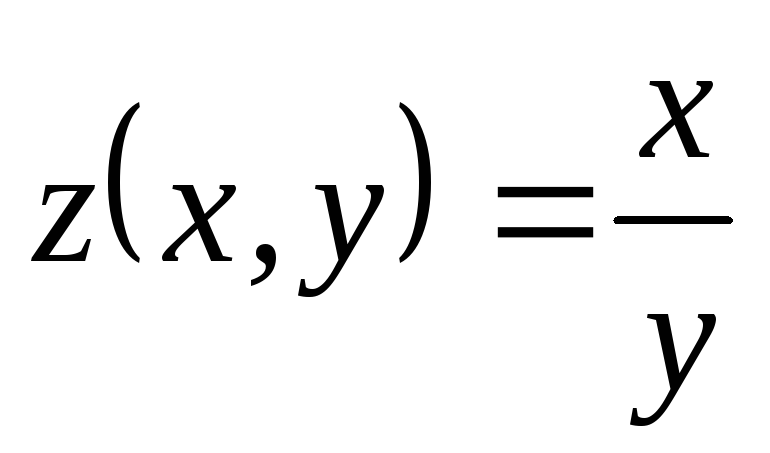 ,
,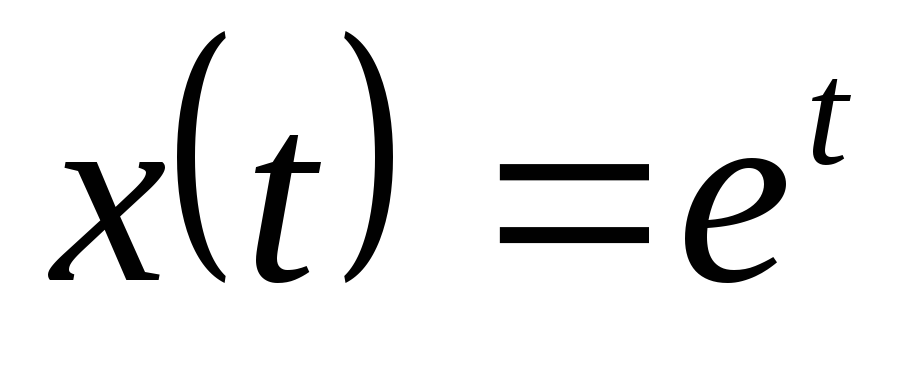 ,
,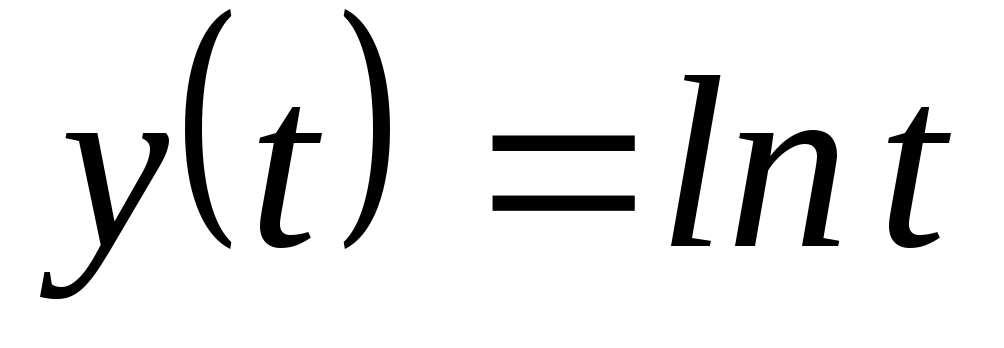 .
Найти
.
Найти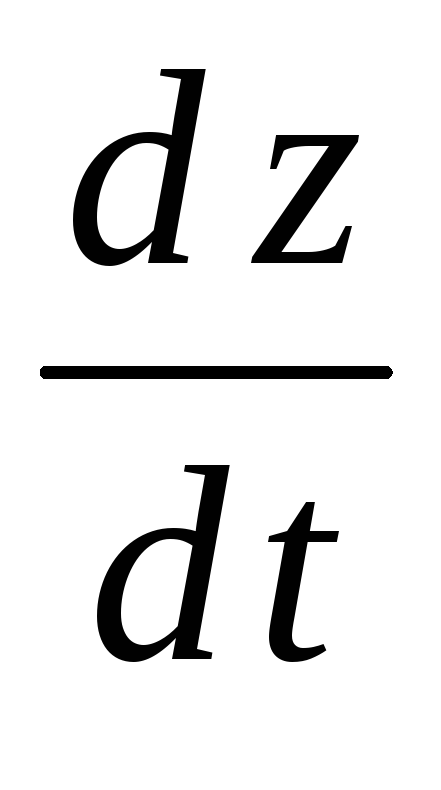 ;
;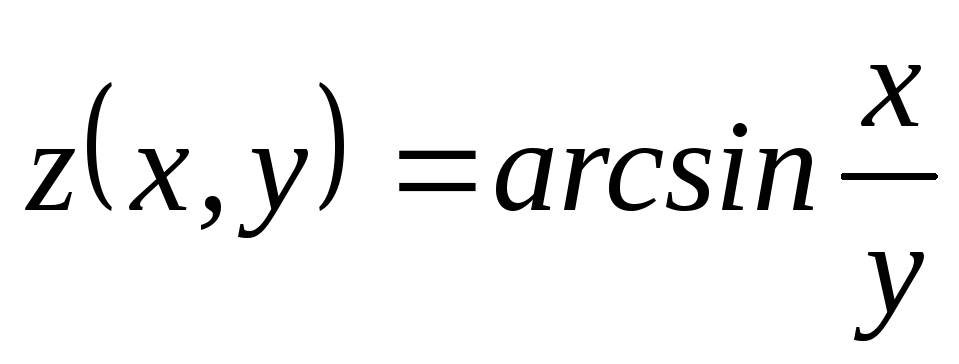 ,
,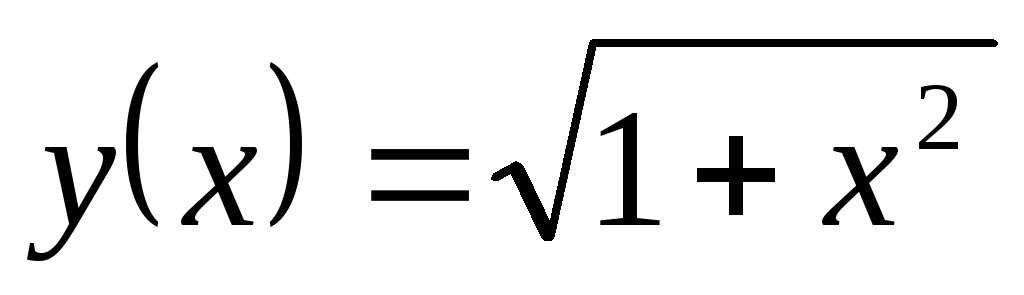 .
Найти
.
Найти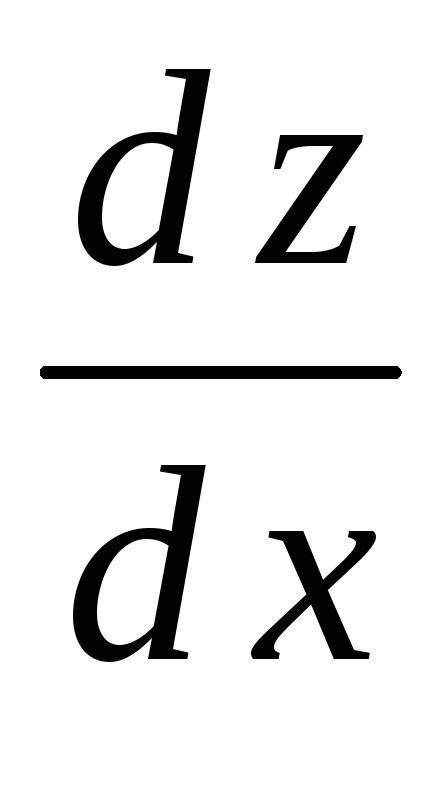 ;
;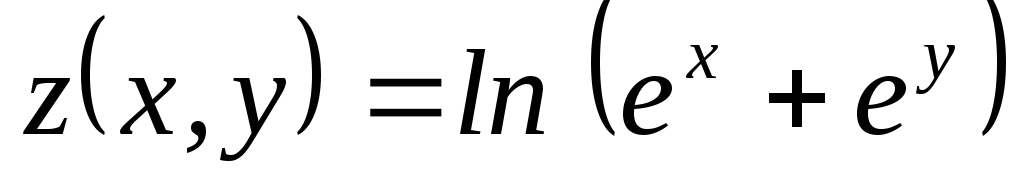 ,
,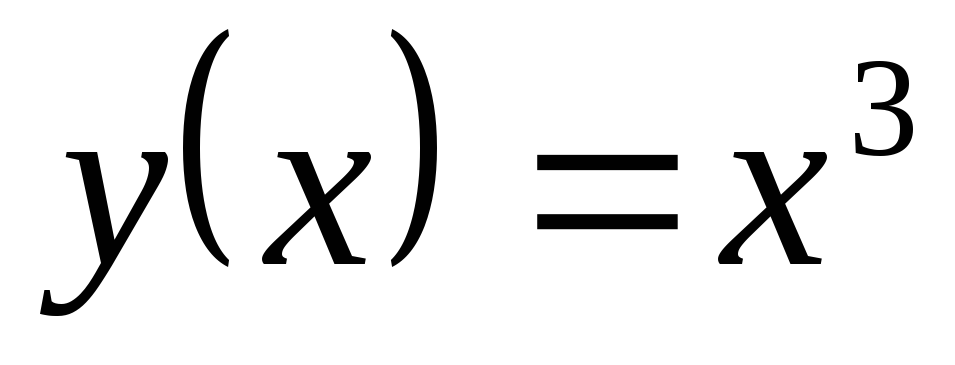 .
Найти
.
Найти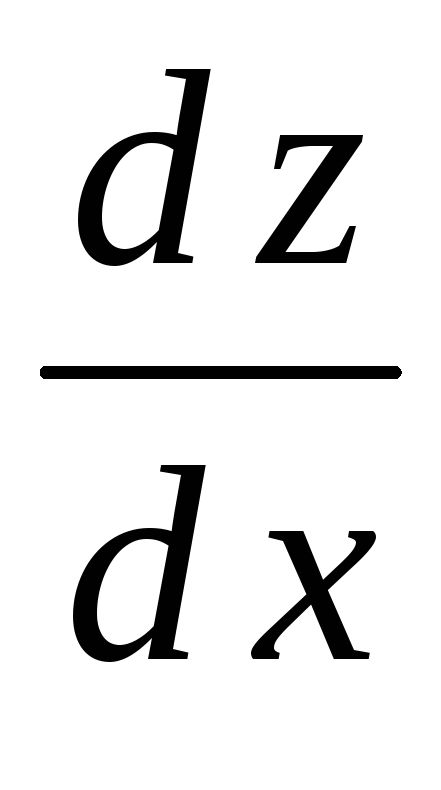 ;
;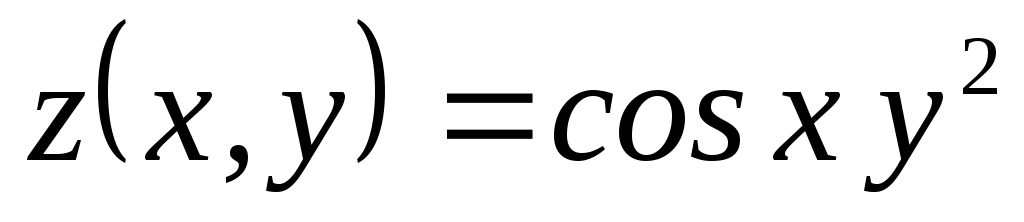 ,
,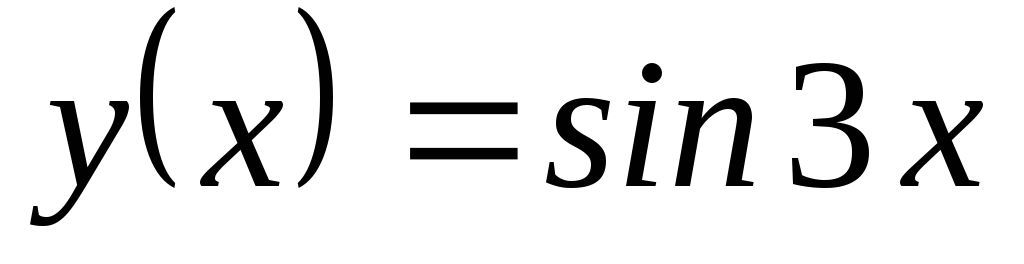 .
Найти
.
Найти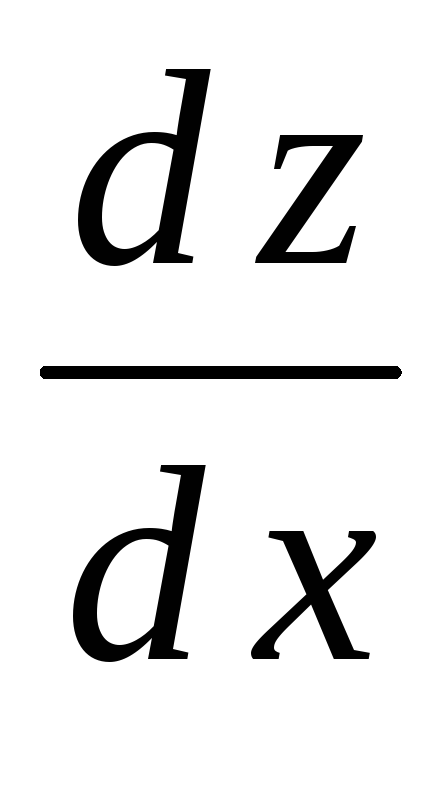 ;
;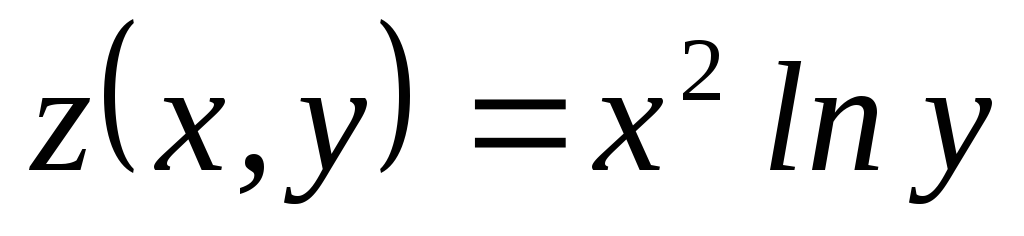 ,
,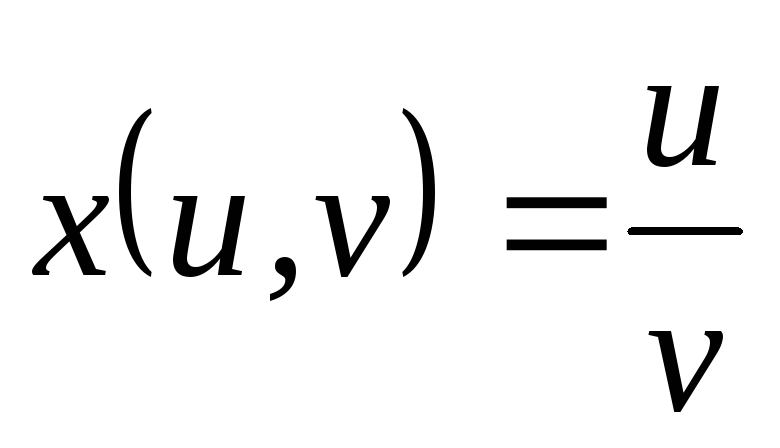 ,
,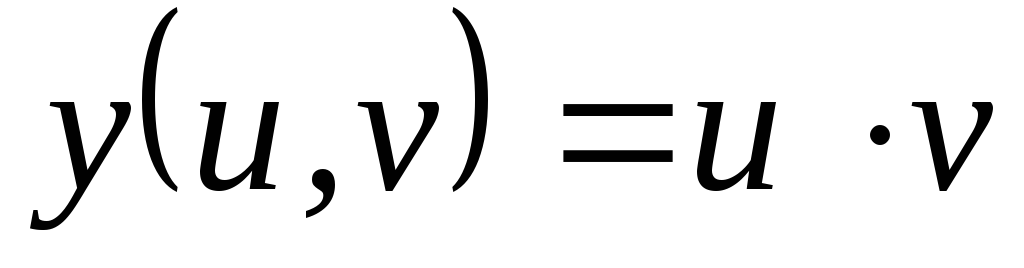 .
Найти
.
Найти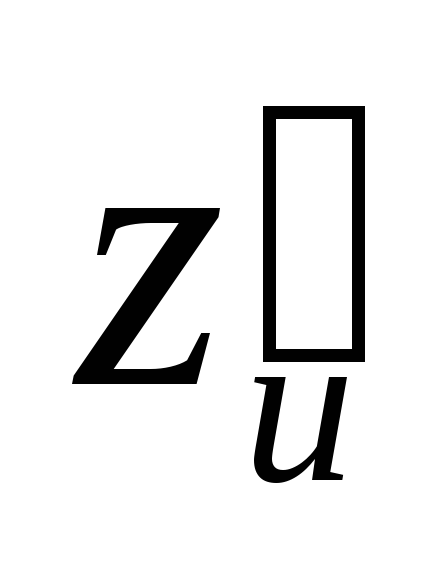 ,
,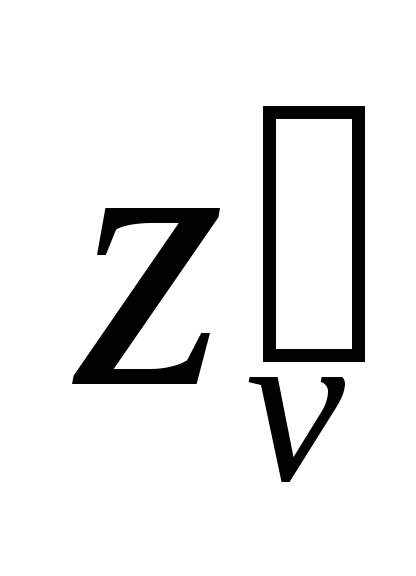 ;
;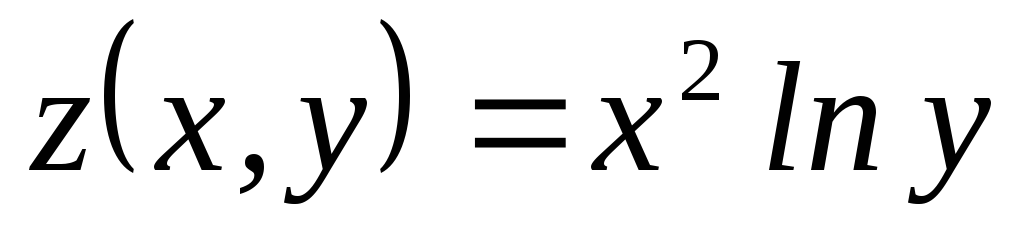 ,
,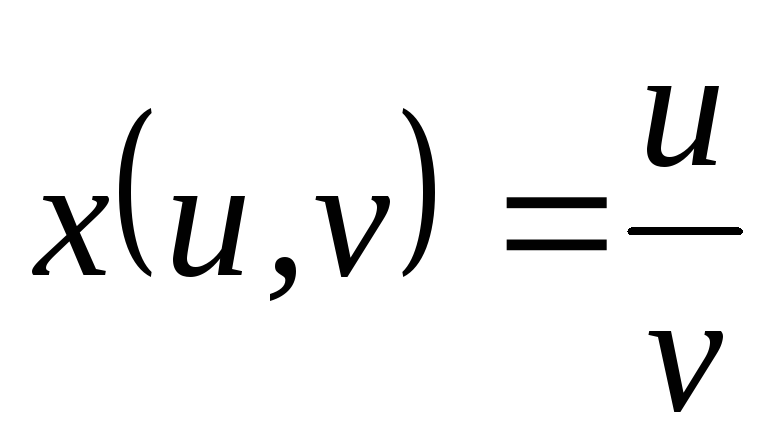 ,
,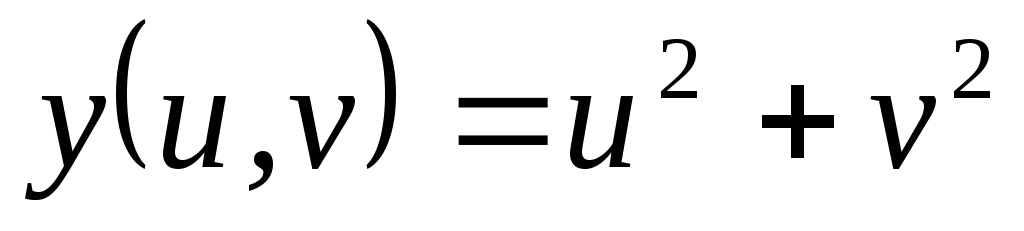 .
Найти
.
Найти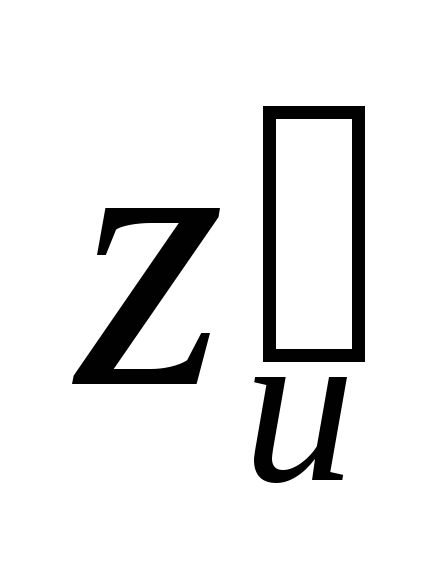 ,
,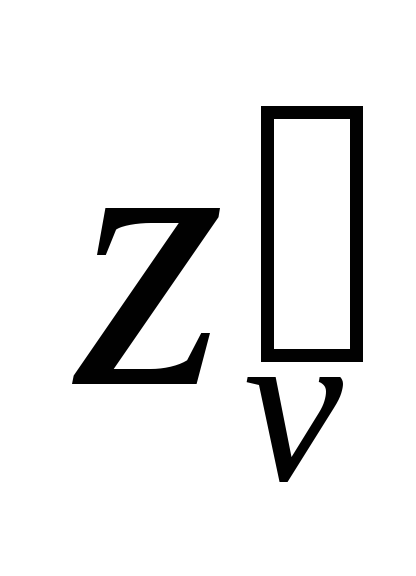 ;
;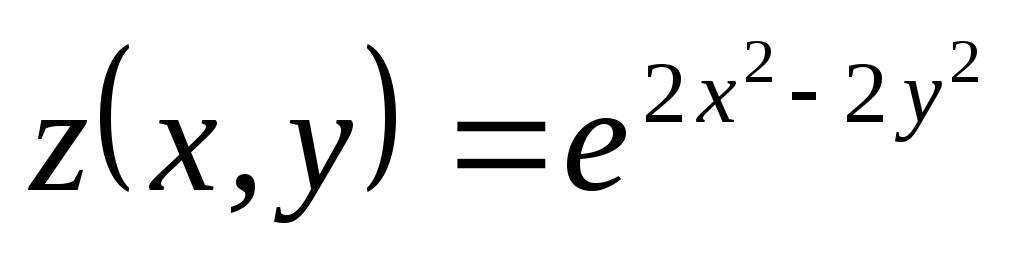 ,
,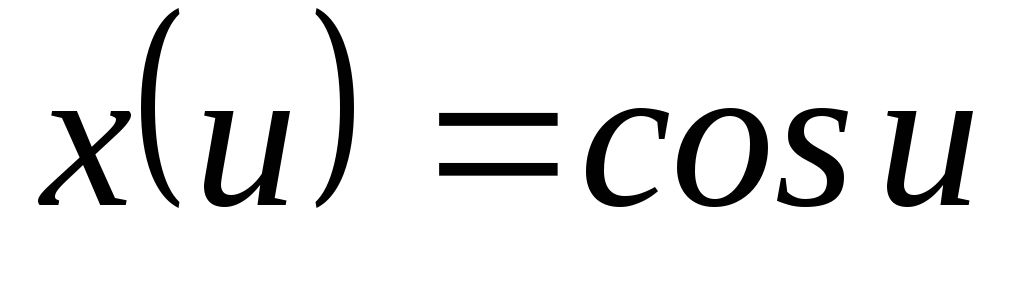 ,
,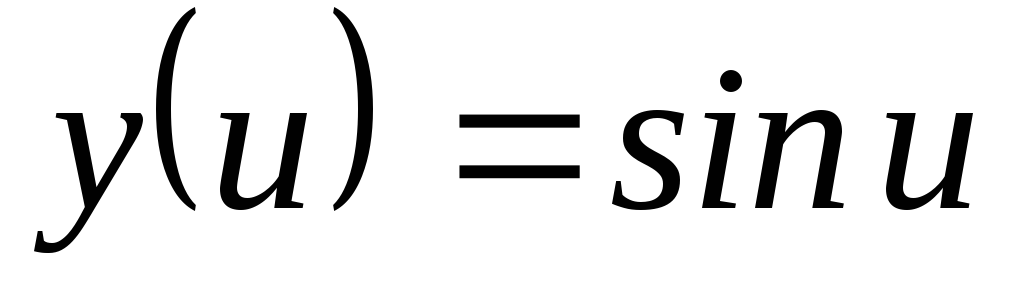 .
Найти
.
Найти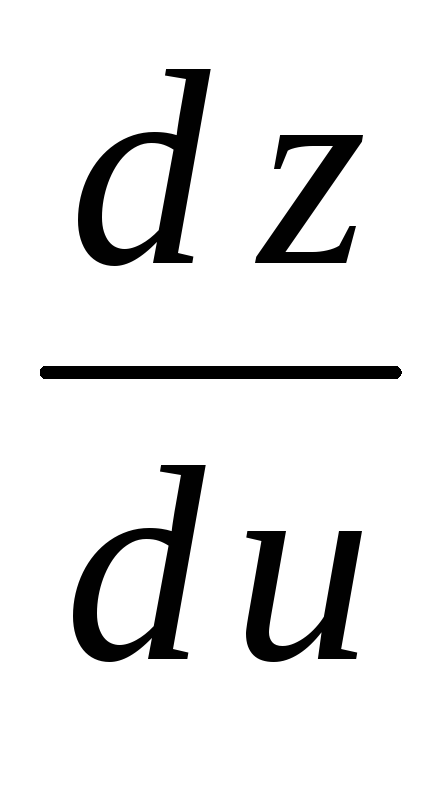 ;
;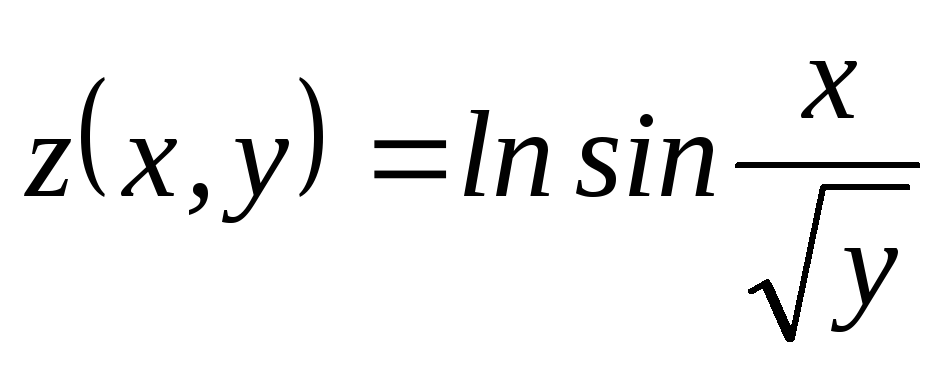 ,
,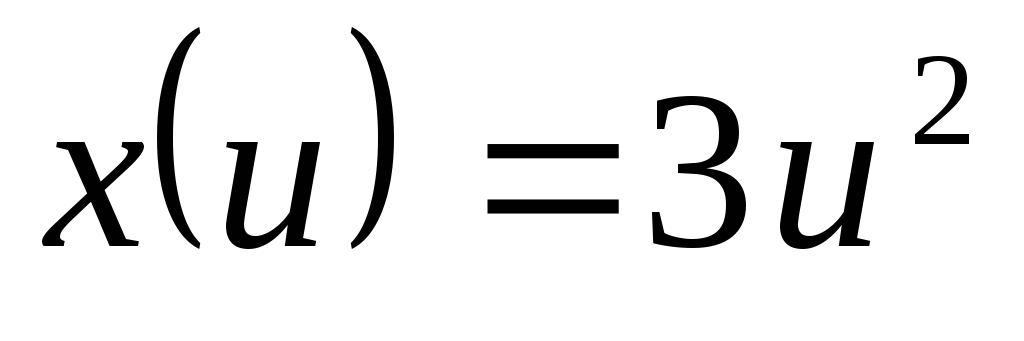 ,
,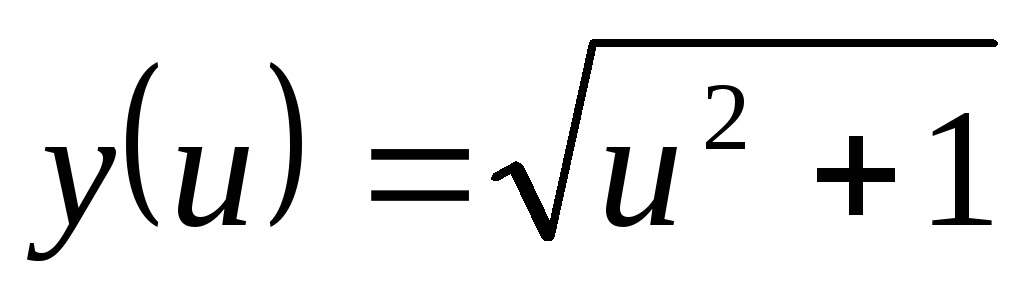 .
Найти
.
Найти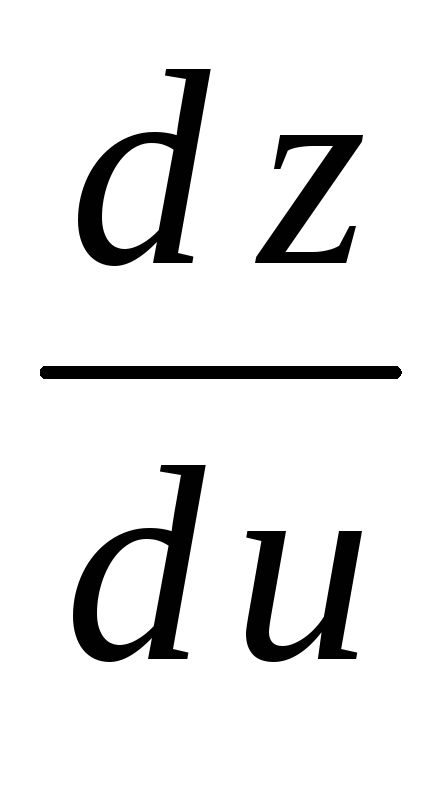 ;
;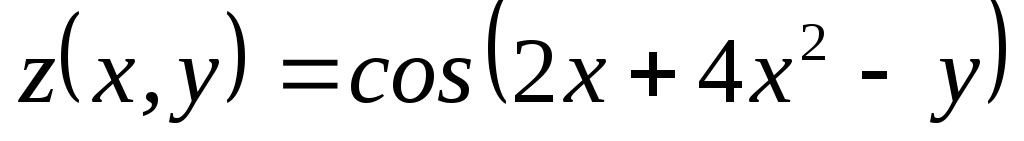 ,
,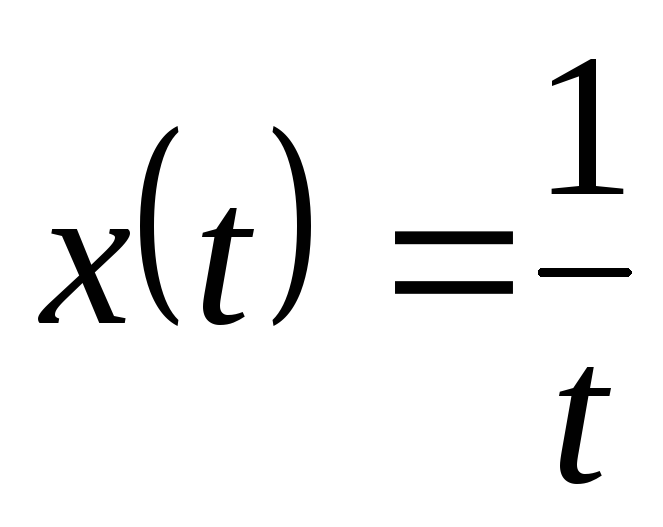 ,
,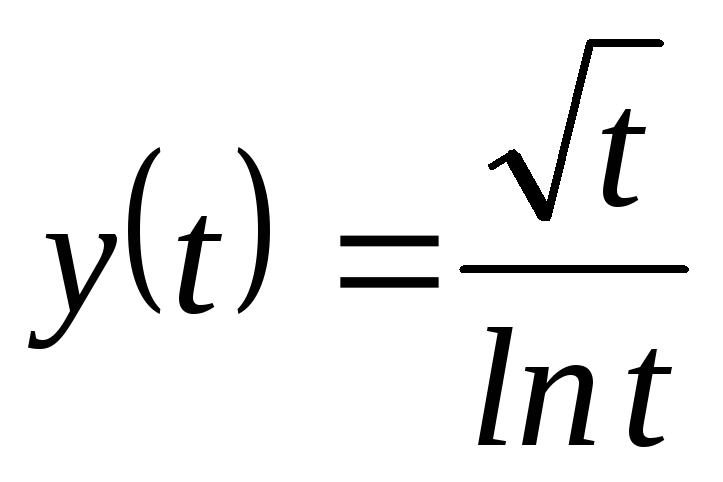 .
Найти
.
Найти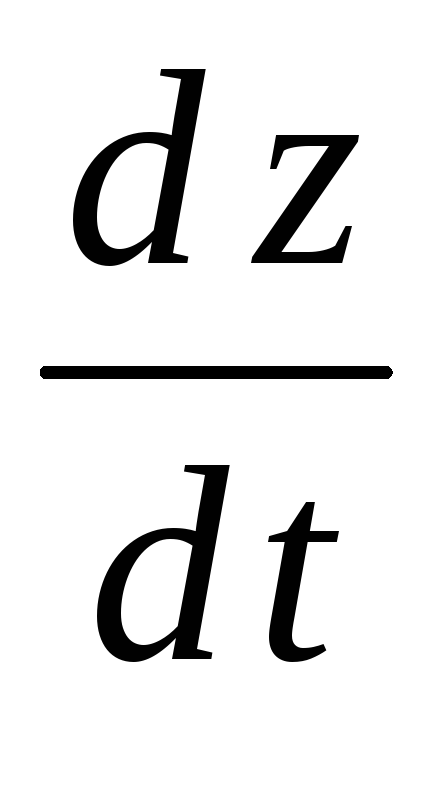 ;
;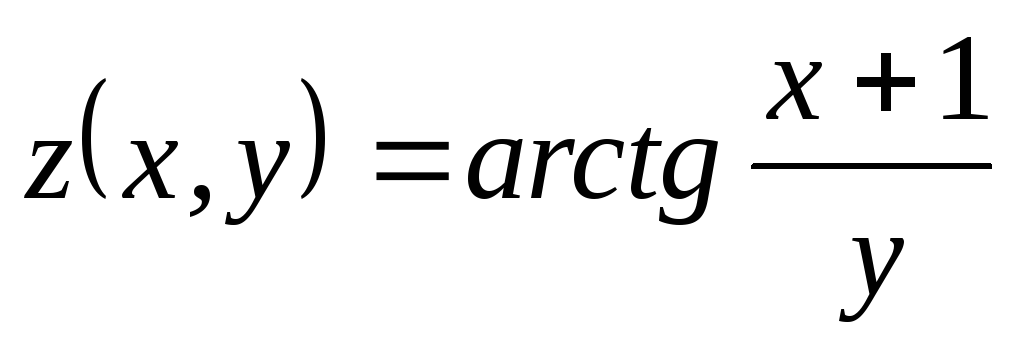 ,
,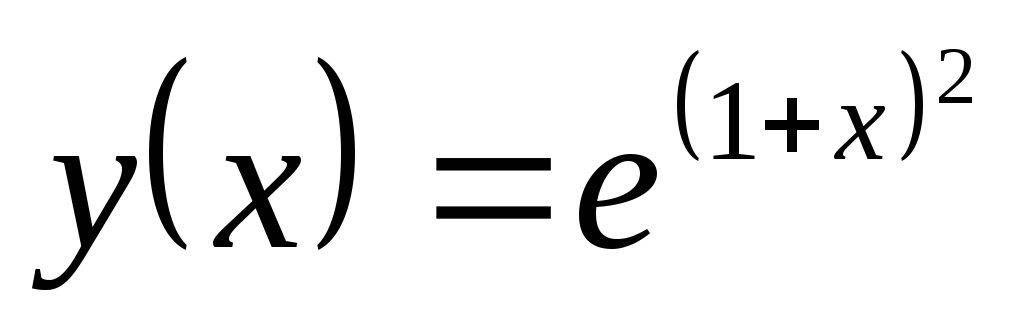 .
Найти
.
Найти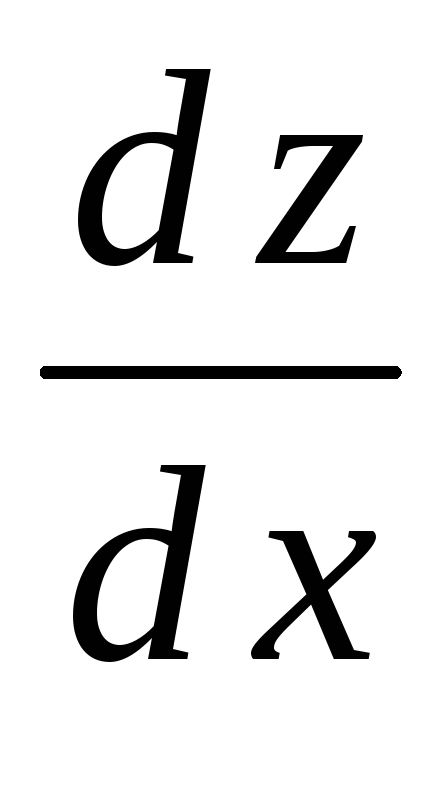 ;
;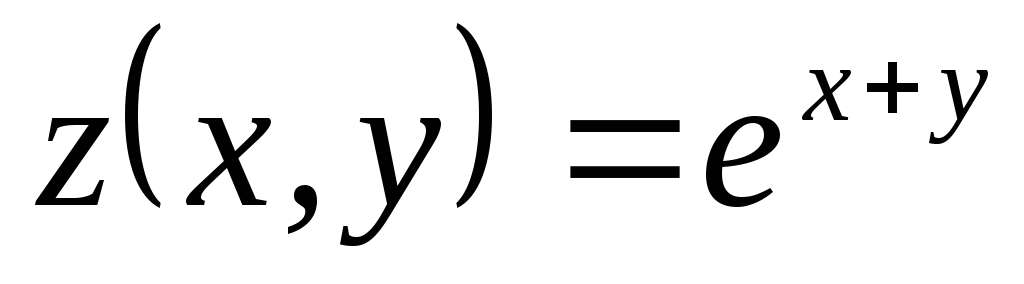 ,
,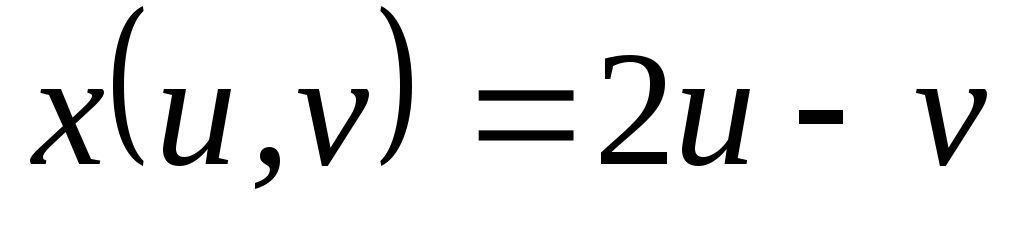 ,
,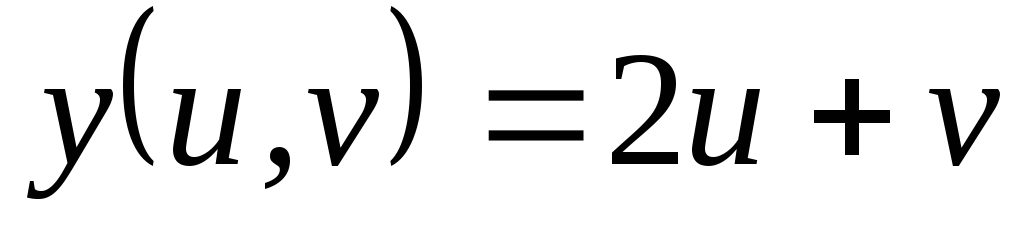 .
Найти
.
Найти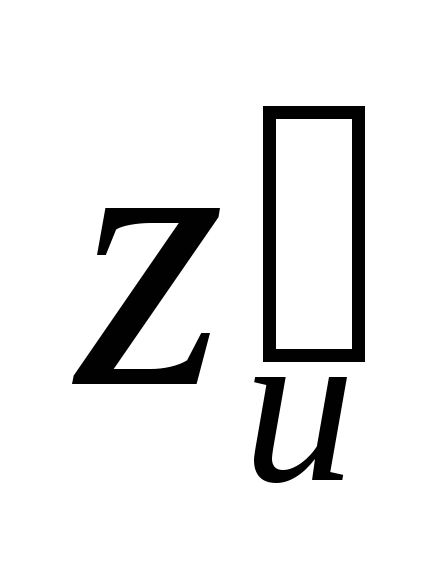 ,
,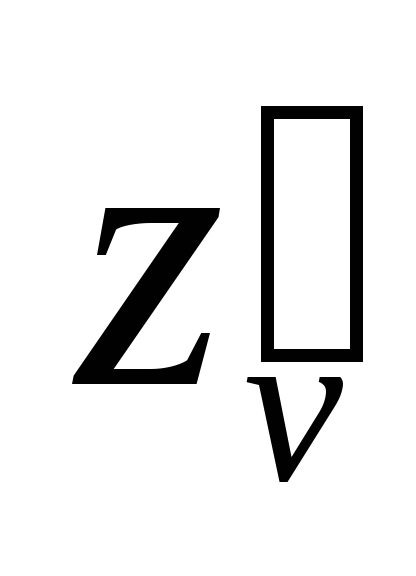 ;
;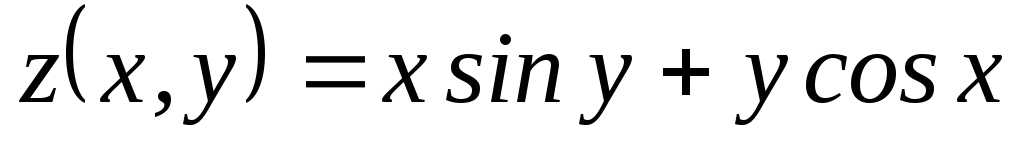 ,
,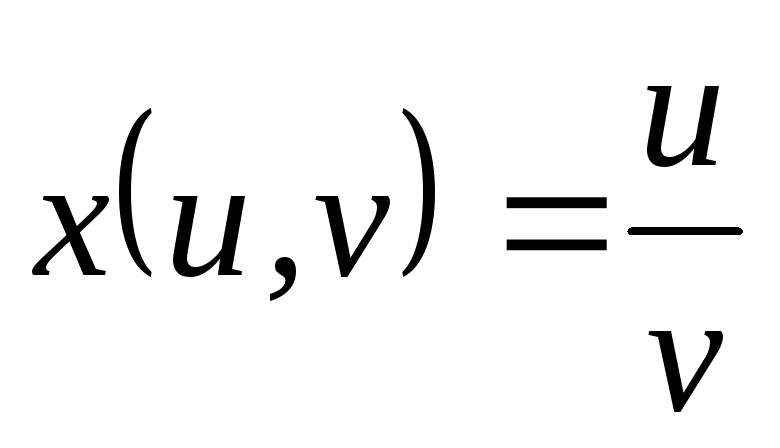 ,
,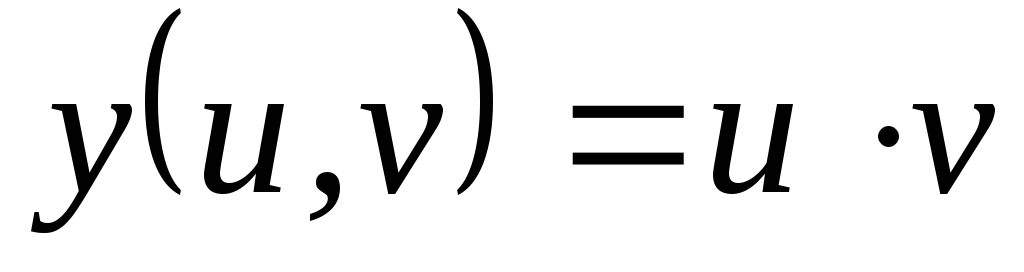 .
Найти
.
Найти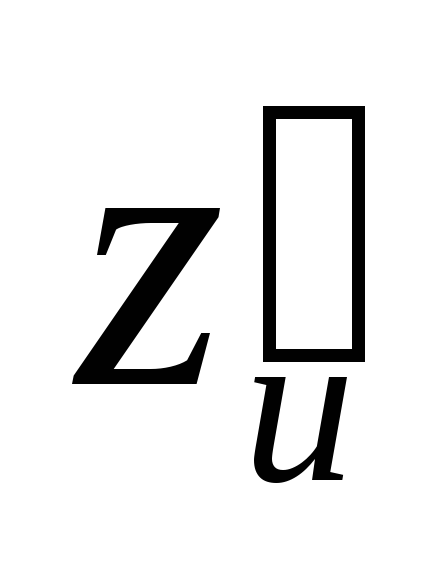 ,
,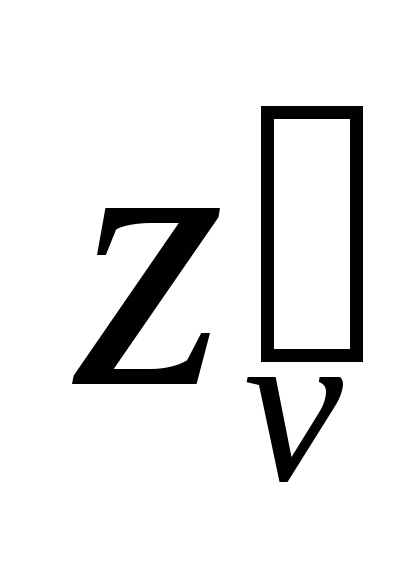 ;
;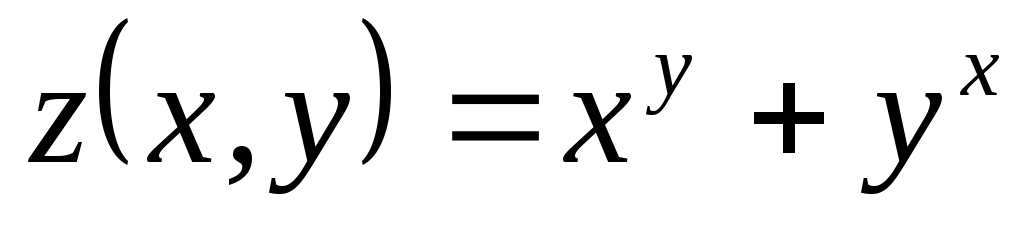 ,
,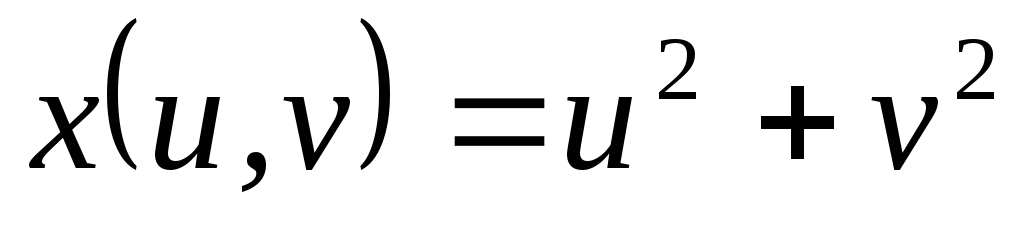 ,
,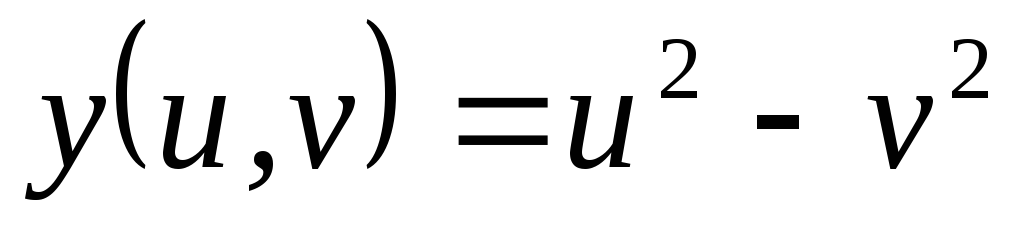 .
Найти
.
Найти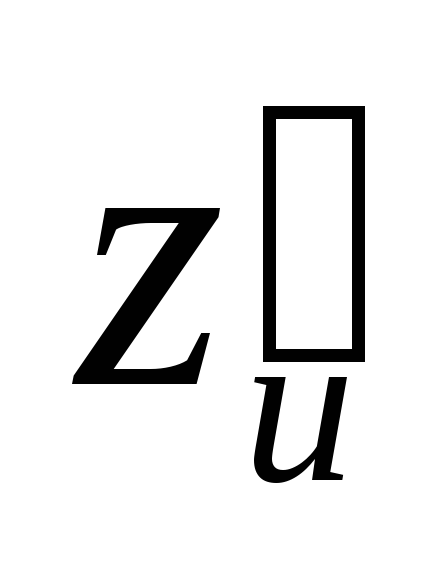 ,
,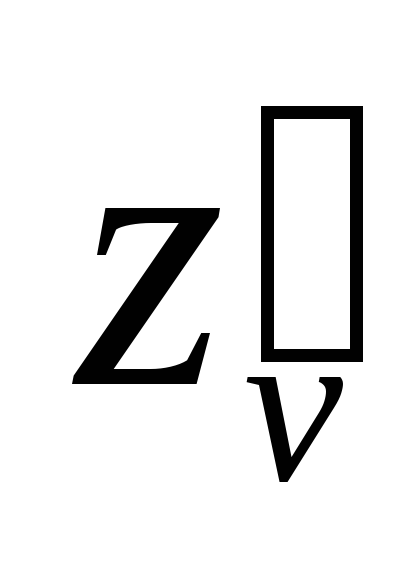 ;
;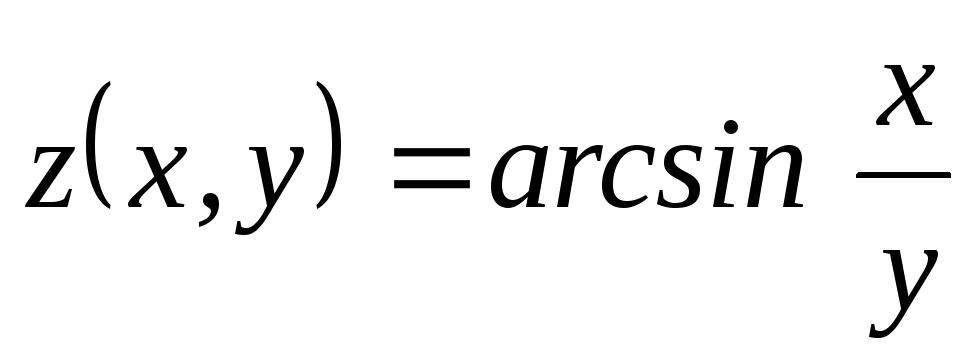 ,
,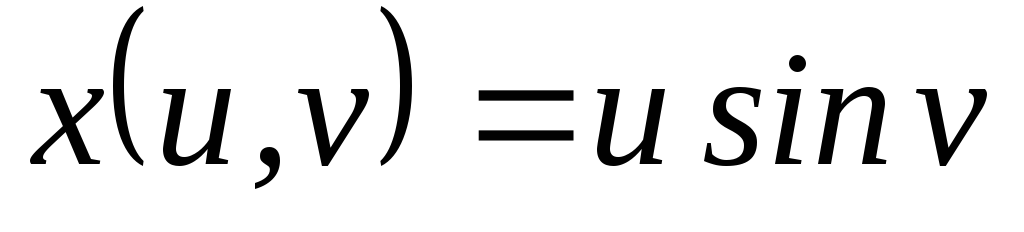 ,
,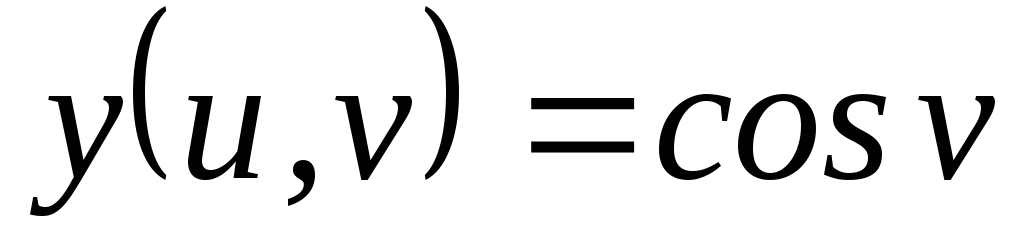 .
Найти
.
Найти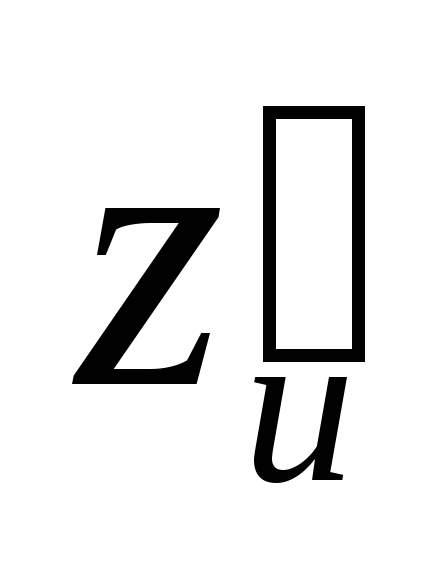 ,
,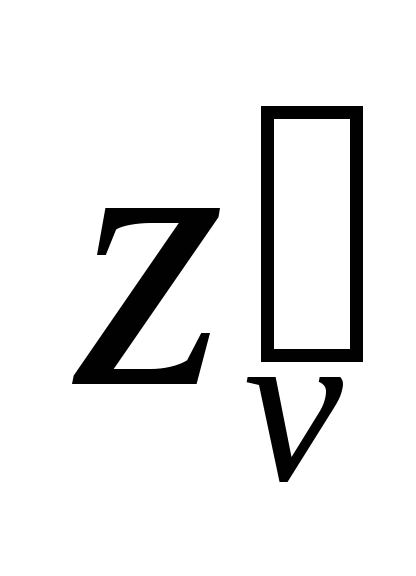 .
.
В задачах 17) – 22) найти производную
![]() неявно заданной функции
неявно заданной функции![]() .
.
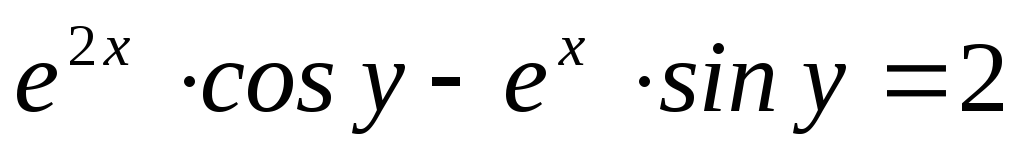 ;
;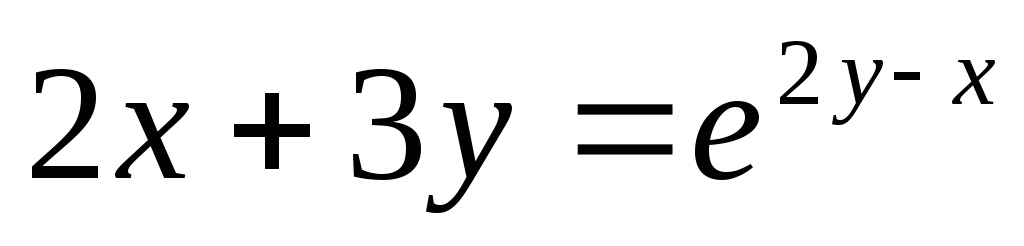 ;
;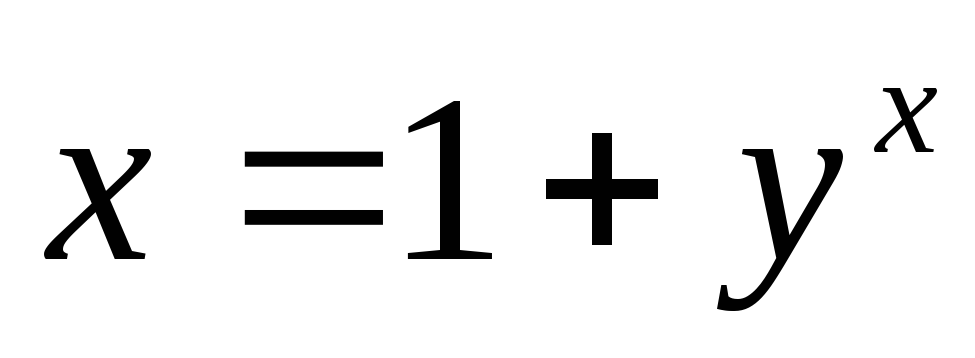 ;
; ;
;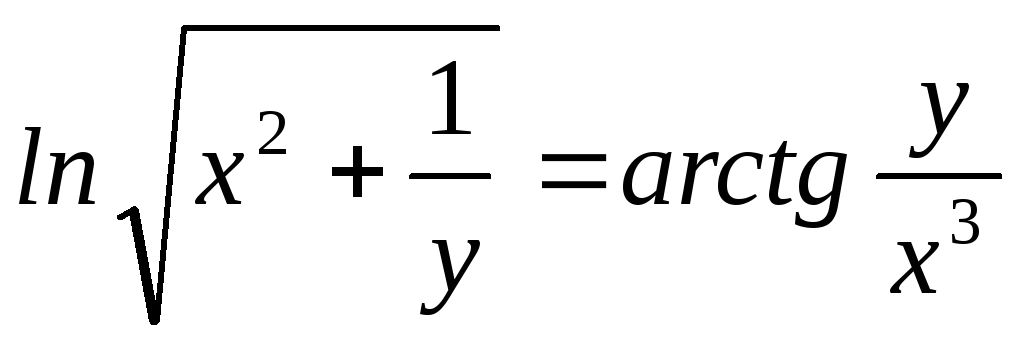 ;
;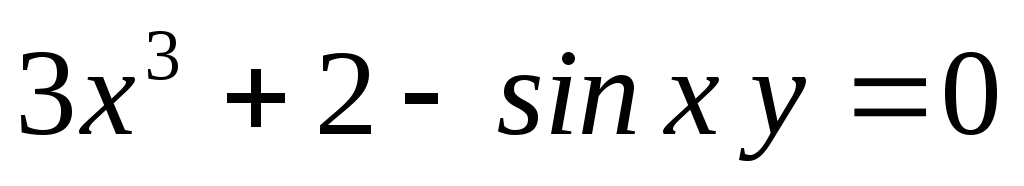 .
.
В задачах 23) – 25) найти
![]() ,
,![]() неявно заданной функции
неявно заданной функции![]() .
.
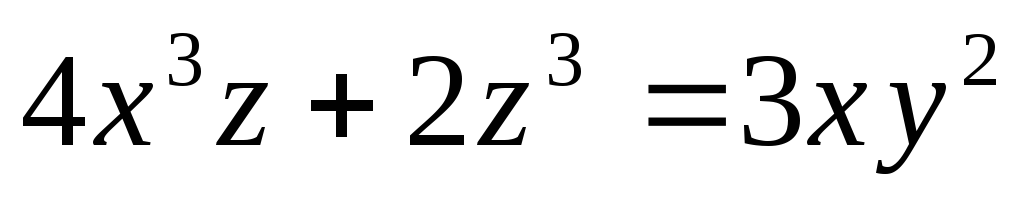 ;
;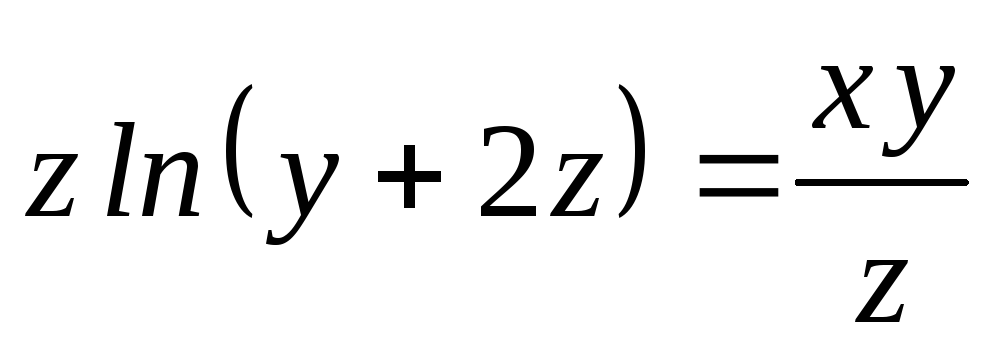 ;
;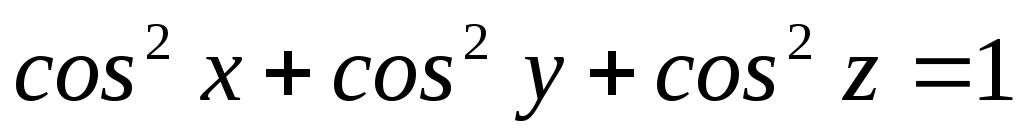 .
.
