
- •Скворцова м.И., Мудракова о.А.
- •Оглавление
- •Занятие 13. Функции двух переменных: основные определения. Частные производные и дифференциал функции двух переменных.
- •Задачи для самостоятельного решения
- •Занятие 14. Производные сложной и неявно заданной функции Производные сложных функций двух переменных
- •Производная неявно заданной функции
- •2) Существуют и.
- •Задачи для самостоятельного решения
- •Занятие 15. Экстремумы функции двух переменных. Элементы теории поля
- •Элементы теории поля
- •Задачи для самостоятельного решения
- •Занятие 16. Контрольная работа №3 по теме «Дифференциальное исчисление функций двух переменных». Вариант-образец.
- •Занятие 17. Метод наименьших квадратов для обработки результатов эксперимента
- •Перечень вариантов для самостоятельной работы по теме «Метод наименьших квадратов»
- •Список литературы
- •Скворцова Мария Ивановна Мудракова Ольга Александровна
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Московская государственная академия
тонкой химической технологии
им. М.В. Ломоносова
Кафедра
высшей и прикладной
математики
Скворцова м.И., Мудракова о.А.
Практикум
по математическому анализу
для студентов вечернего отделения
1-ого курса
(Часть III)
Учебно-методическое пособие
Москва, 2007
УДК 512.8:516
ББК С42
Рецензенты:
к.ф.-м.н., доцент Каролинская С.Н. (Московский авиационный институт им. С. Орджоникидзе);
к.ф.-м.н., доцент Краснослободцева Т.П. (МГАТХТ им. М.В. Ломоносова).
Скворцова М.И., Мудракова О.А.Практикум по математическому анализу для студентов вечернего отделения 1-ого курса (ЧастьIII), Учебно-методическое пособие – М.: МГАТХТ, 2007 – 48 с.; рис. 5.
Пособие представляет собой конспекты 5 практических занятий по курсу математического анализа для студентов вечернего отделения МИТХТ им. М.В. Ломоносова. Оно является продолжением учебно-методического пособия: Скворцова М. И., Мудракова О. А., Кротов Г.С. // Практикум по математическому анализу для студентов вечернего отделения 1-ого курса (Часть II); М., МГАТХТ, 2006.В частьIIIвключены следующие разделы: «Дифференциальное исчисление функций двух переменных», «Метод наименьших квадратов». Каждое занятие посвящено отдельной теме. Конспекты 4-х занятий содержат краткое изложение соответствующей теории, типовые примеры и задачи для самостоятельного решения. В конспекте одного из занятий приведен образец варианта контрольной работы (с решениями), проводимой на этом занятии. Дан перечень 28 вариантов задания для самостоятельной работы по теме «Метод наименьших квадратов» (с ответами).
Пособие предназначено для студентов вечернего и очно-заочно отделений вузов химического профиля. Оно может быть использовано также и студентами дневного отделения вузов вышеуказанного профиля.
© МИТХТ им. М.В. Ломоносова, 2007
Оглавление
Занятие 13. Функции двух переменных: основные определения. Частные производные и дифференциал функции двух переменных. 4
Занятие 14. Производные сложной и неявно заданной функции 15
Занятие 15. Экстремумы функции двух переменных. Элементы теории поля 22
Занятие 16. Контрольная работа №3 по теме «Дифференциальное исчисление функций двух переменных». Вариант-образец. 33
Список литературы 46
Занятие 13. Функции двух переменных: основные определения. Частные производные и дифференциал функции двух переменных.
Определение. Пусть на плоскости![]() задано некоторое множество
задано некоторое множество![]() .
Зависимость переменной
.
Зависимость переменной![]() от переменных
от переменных![]() и
и![]() называетсяфункцией двух переменных,
если каждой паре чисел
называетсяфункцией двух переменных,
если каждой паре чисел![]() ставится в соответствие единственное
значение
ставится в соответствие единственное
значение![]() .
.
Пишем:![]() .
.
Говорим:![]() есть функция от
есть функция от![]() и
и![]() .
.
При этом
![]() и
и![]() называются независимыми переменными
(аргументами), а
называются независимыми переменными
(аргументами), а![]() – зависимой переменной.
– зависимой переменной.
Определения.
Область определения функции
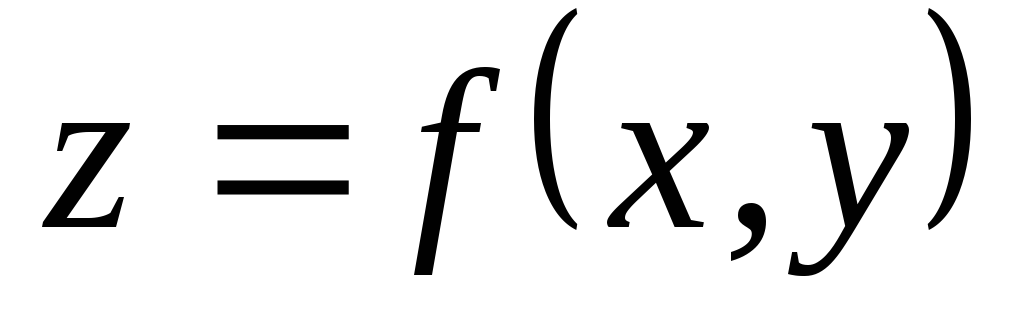 – это множество всех пар
– это множество всех пар ,
для которых она определена, т.е. множество
,
для которых она определена, т.е. множество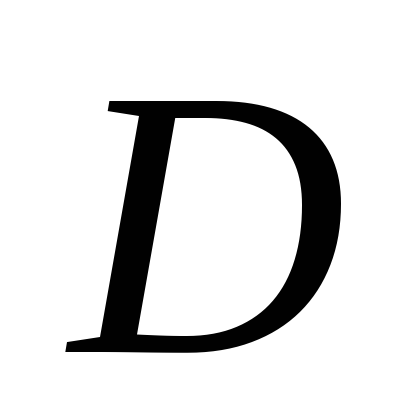 ;
;Множество значений функции
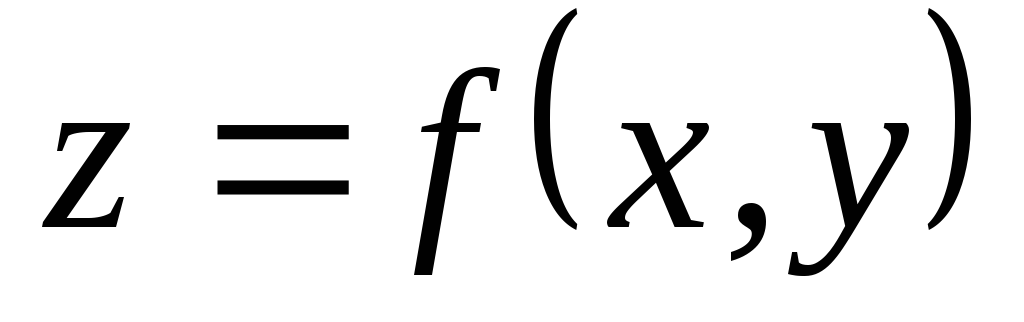 – это множество
– это множество
![]() ;
;
График функции
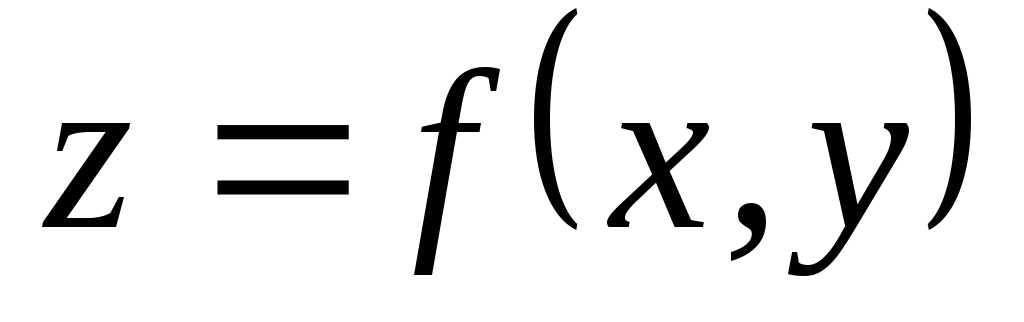 – это множество точек
– это множество точек ,
таких, что
,
таких, что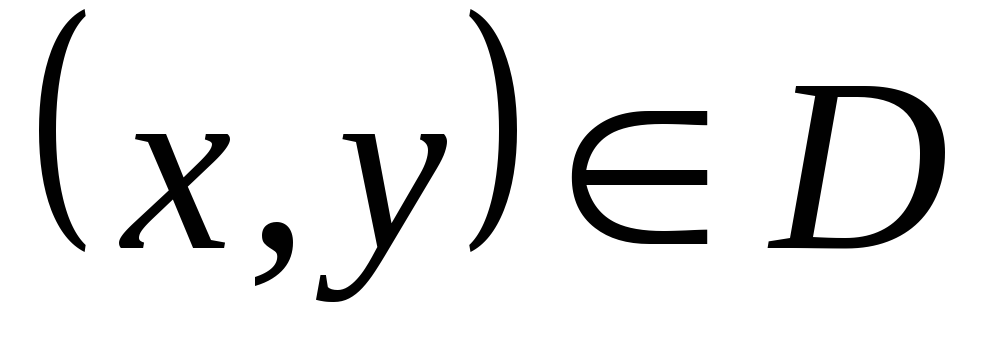 ,
а
,
а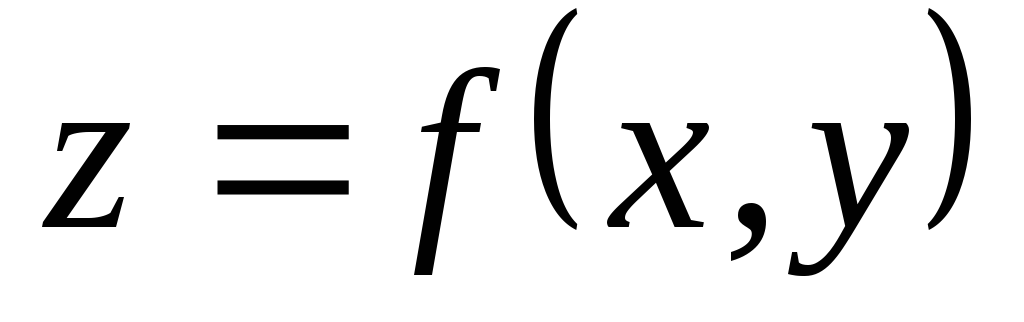 (это поверхность в
(это поверхность в ).
).
Пример 1 (Определение множеств
![]() и построение графика функции).
и построение графика функции).
Рассмотрим функцию
![]() .
.
Область определения этой функции:
![]() –
–
круг радиуса
![]() с центром в точке
с центром в точке![]() .
Множество значений функции:
.
Множество значений функции:![]() – отрезок.
– отрезок.
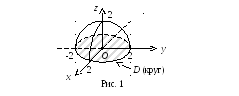
График функции
![]() – это верхняя часть сферы радиуса
– это верхняя часть сферы радиуса![]() с центром в точке
с центром в точке![]() (рис. 1).
(рис. 1).
Пример 2 (Определение области
![]() и изображение ее
и изображение ее
на плоскости).
Рассмотрим функцию
![]() .
.
Найдем ее область определения
![]() .
Т.к. функция «логарифм» определена
только для положительных значений
аргумента, то
.
Т.к. функция «логарифм» определена
только для положительных значений
аргумента, то
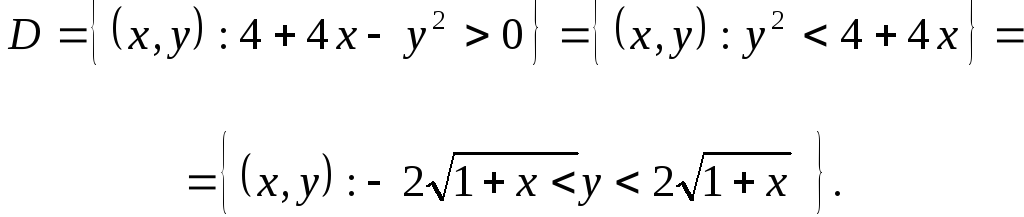
Изобразим
![]() на плоскости:
на плоскости:
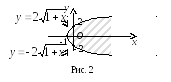
Пример 3 (Определение области
![]() и изображение ее
и изображение ее
на плоскости).
Рассмотрим функцию
![]() .
.
Найдем ее область определения
![]() .
Т.к. функция «арксинус» определена
только для значений аргумента,
принадлежащих отрезку
.
Т.к. функция «арксинус» определена
только для значений аргумента,
принадлежащих отрезку![]() ,
то
,
то![]() .
Т.к. функция «квадратный корень»
определена для неотрицательных значений
подкоренного выражения, то
.
Т.к. функция «квадратный корень»
определена для неотрицательных значений
подкоренного выражения, то![]() .
Имеем систему неравенств, задающую
область
.
Имеем систему неравенств, задающую
область![]() :
:
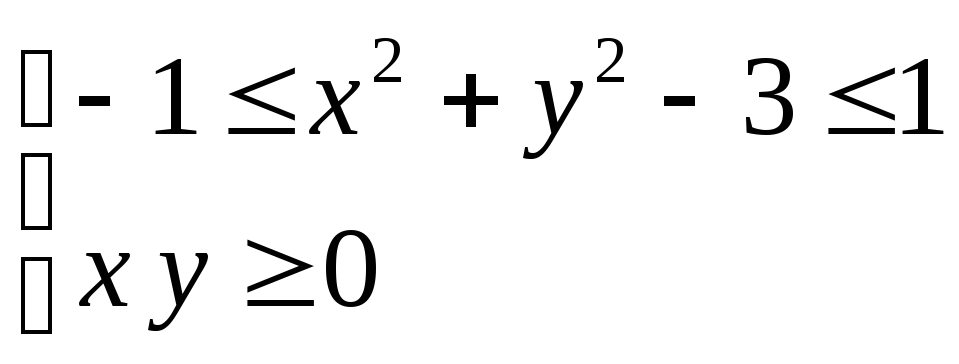
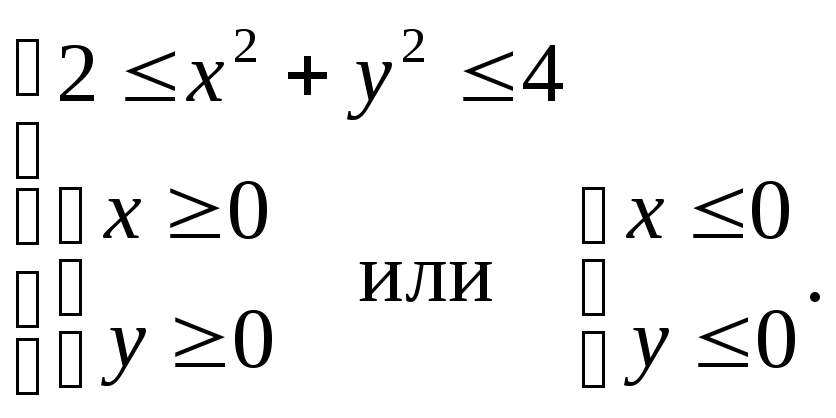
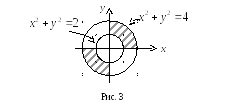
На рис. 3 изображена область
![]() ,
представляющая собой две части кольца,
ограниченного окружностями
,
представляющая собой две части кольца,
ограниченного окружностями![]() и
и![]() ,
расположенных вI-ой иIII-ей четвертях координатной
плоскости.
,
расположенных вI-ой иIII-ей четвертях координатной
плоскости.
* * * * *
Значение функции
![]() в некоторой конкретной точке
в некоторой конкретной точке![]() обозначатся:
обозначатся:
![]() или
или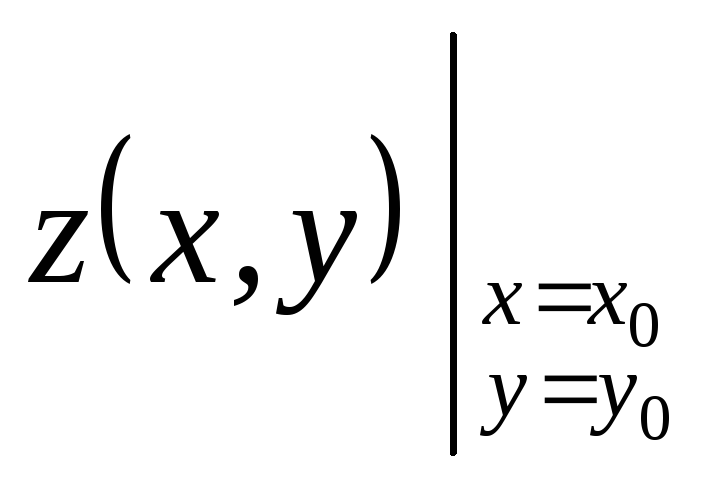 .
.
Пример 4 (Нахождение значения функции в точке).
Для функции
![]() и точек:
и точек:
а) ![]() ;б)
;б) ![]() ;в)
;в) ![]() найти значение
найти значение![]() .
.
Подставим в выражение для
![]() вместо
вместо![]() и
и![]() заданные значения
заданные значения![]() и
и![]() :
:
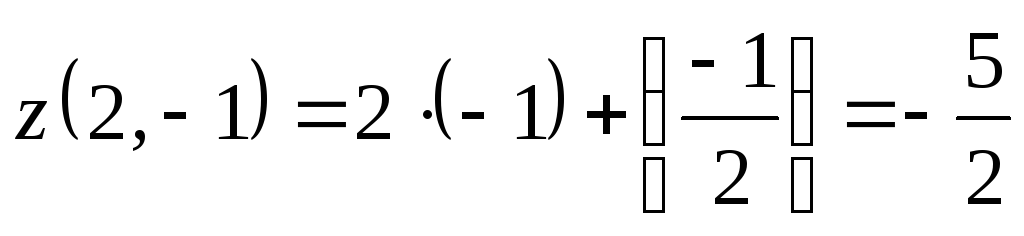 ;
;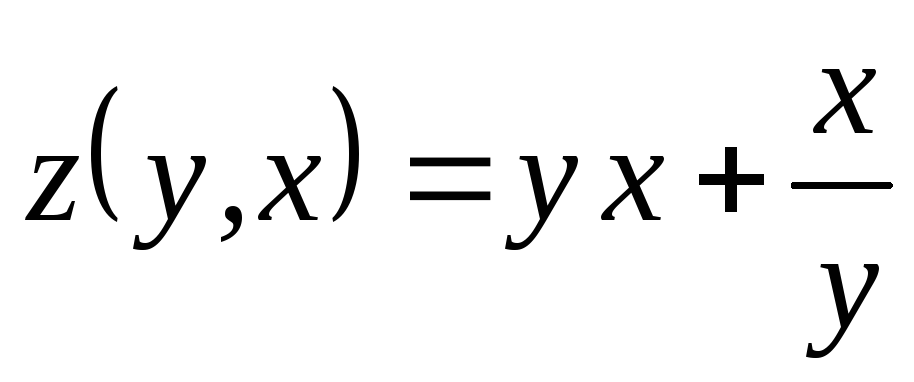 ;
; .
.
Определение. Частной производной
![]() (читаем: «зэт штрих по икс») функции
(читаем: «зэт штрих по икс») функции![]() по переменной
по переменной![]() называется следующий предел:
называется следующий предел:
![]() .
.
Аналогично определяется частная
производная
![]() (читаем: «зэт штрих по игрек»):
(читаем: «зэт штрих по игрек»):
![]() .
.
Для частных производных, наряду с
![]() ,
,
![]() ,
используются также следующие обозначения:
,
используются также следующие обозначения:
![]() .
.
(или
![]() ).
).
Запись «![]() »
читаем «дэ эф по дэ икс».
»
читаем «дэ эф по дэ икс».
Значение частной производной
![]() в некоторой фиксированной точке
в некоторой фиксированной точке![]() обозначаем так:
обозначаем так:
или
![]() ,
или
,
или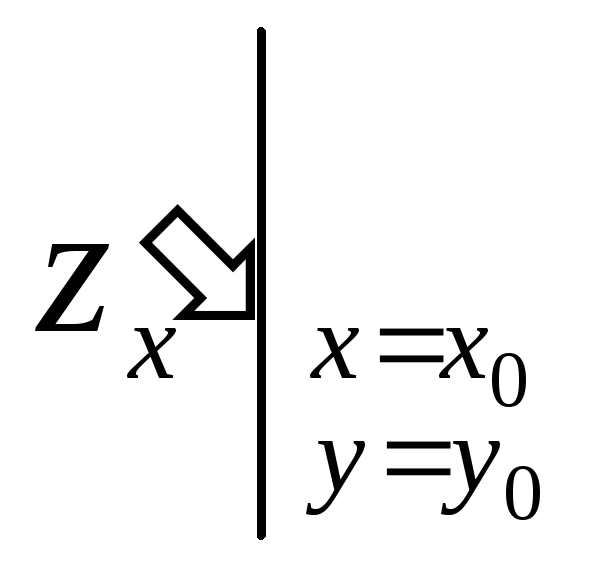 ,
или
,
или![]() .
.
Определение. Полный дифференциал
![]() функции
функции![]() в точке
в точке![]() – это выражение вида:
– это выражение вида:
![]() ,
,
где
![]() ,d y
≡Δy- приращения
аргументов
,d y
≡Δy- приращения
аргументов![]() и
и![]() .
(Таким образом,
.
(Таким образом,![]() зависит от заданной точки
зависит от заданной точки![]() и заданных приращений
и заданных приращений![]() ,
,![]() аргументов
аргументов![]() и
и![]() ).
).
Определение. Частные производные
2-го порядка от функции![]() – это частные производные по
– это частные производные по![]() или по
или по![]() от функций
от функций![]() и
и![]() ,
т.е.:
,
т.е.:
![]() ,
,![]() ;
;![]() ,
,![]()
или, в других обозначениях:
![]() ,
,![]() ,
,![]() ,
,
![]() .
.
Замечания.
Частные производные
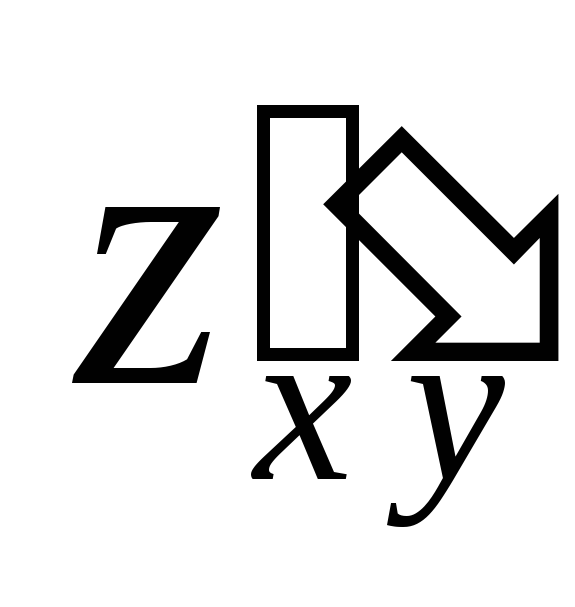 и
и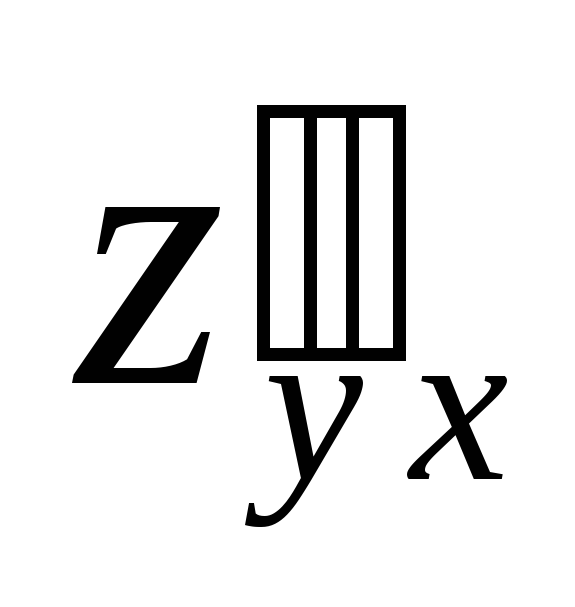 называют смешанными частными производными.
называют смешанными частными производными.
Если
![]() определена в некоторой области
определена в некоторой области![]() и ее частные производные
и ее частные производные![]() ,
,![]() ,
,![]() ,
,![]() определены и непрерывны в
определены и непрерывны в![]() ,
то
,
то![]() (теорема Шварца).
(теорема Шварца).
Аналогично определяется функция
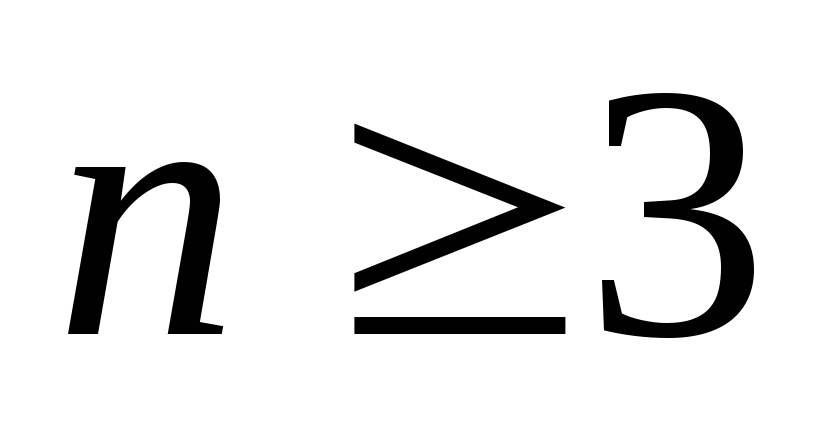 переменных
переменных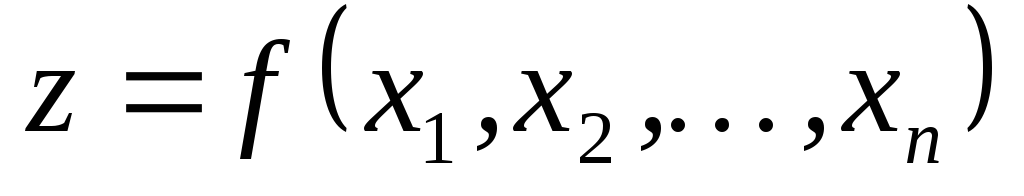 и ее частные производные
и ее частные производные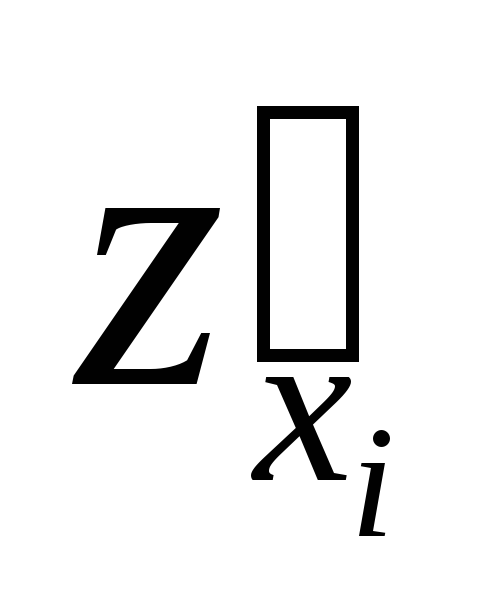 или
или
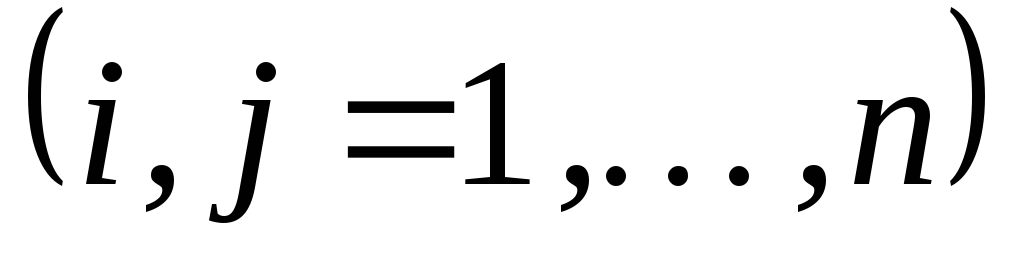 .
.
Пример 5 (Вычисление
![]() ,
,![]() и
и![]() ).
).
В процессе нахождения частной производной
![]() полагаем, что вторая переменная
полагаем, что вторая переменная![]() – это константа. В этом случае нахождение
– это константа. В этом случае нахождение![]() сводится к нахождению обычной производной
от функции одной переменной
сводится к нахождению обычной производной
от функции одной переменной![]() с соблюдением всех правил дифференцирования.
Аналогичное верно и для
с соблюдением всех правил дифференцирования.
Аналогичное верно и для![]() .
.
Найдем
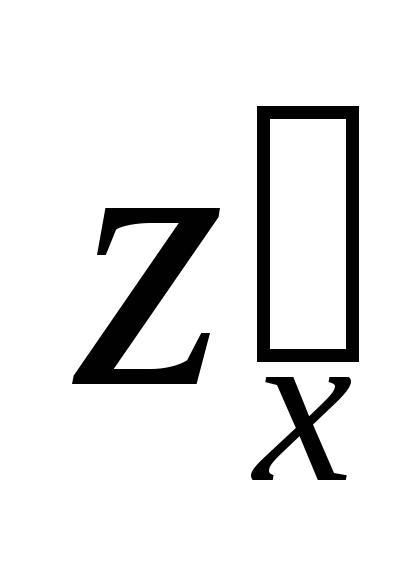 ,
,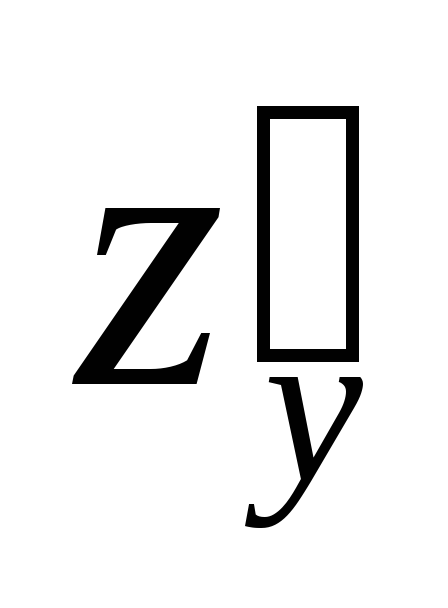 и
и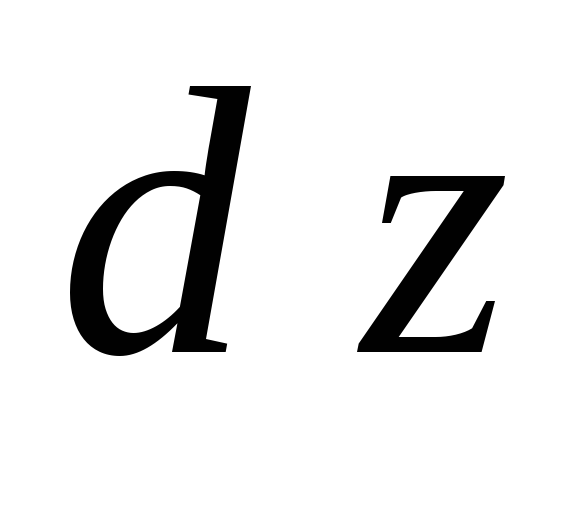 для функции
для функции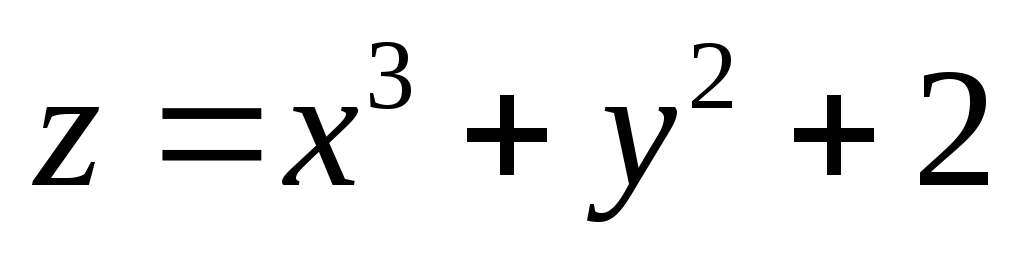 .
.
Имеем:
![]() ;
;
![]() ;
;
![]() .
.
Найдем
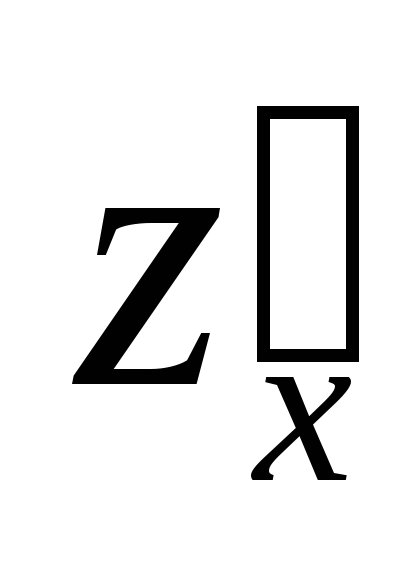 ,
,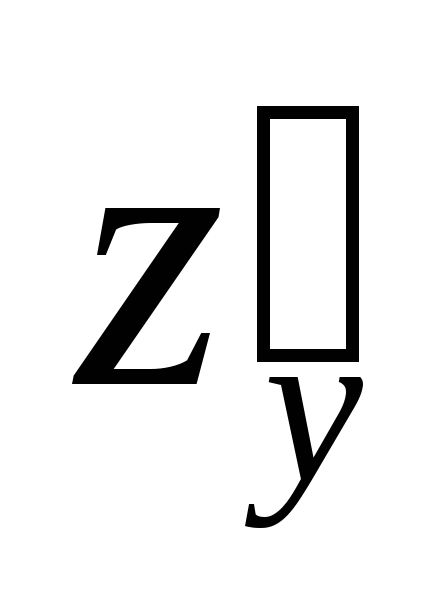 и
и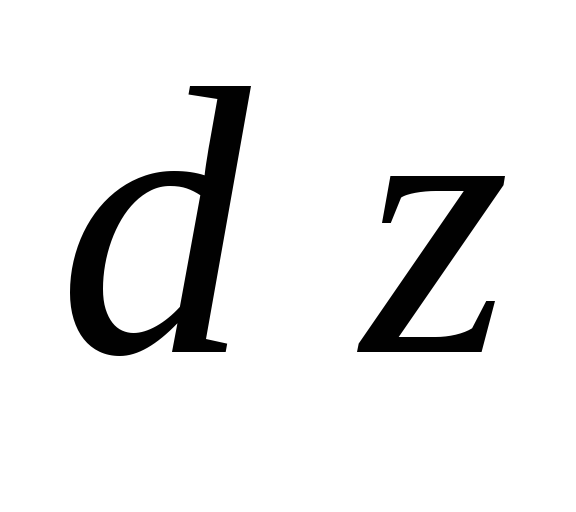 для функции
для функции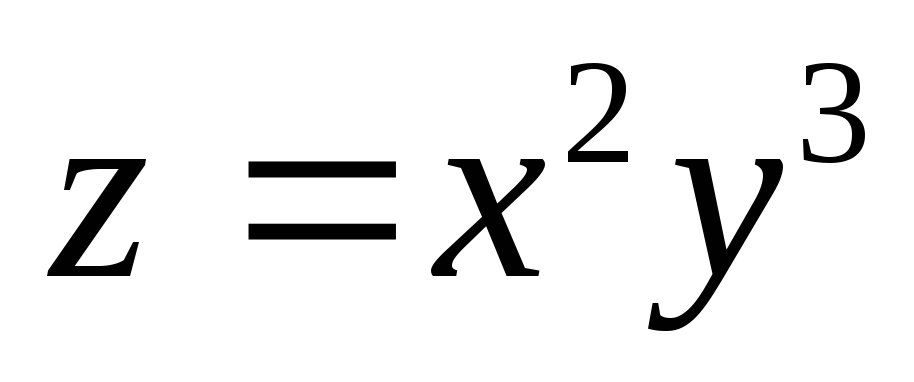 .
.
Имеем:
![]() ;
;
![]() ;
;
![]() .
.
Найдем
 ,
,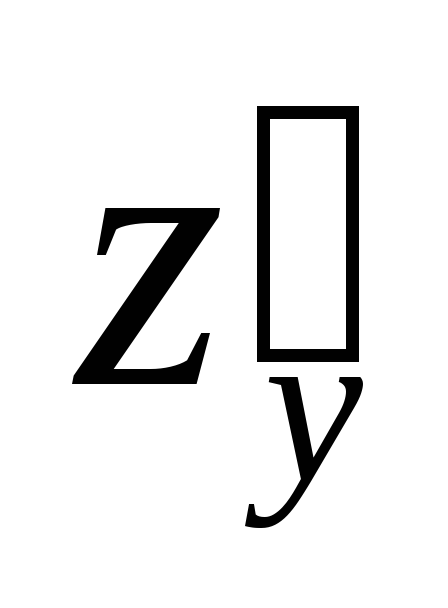 для функции
для функции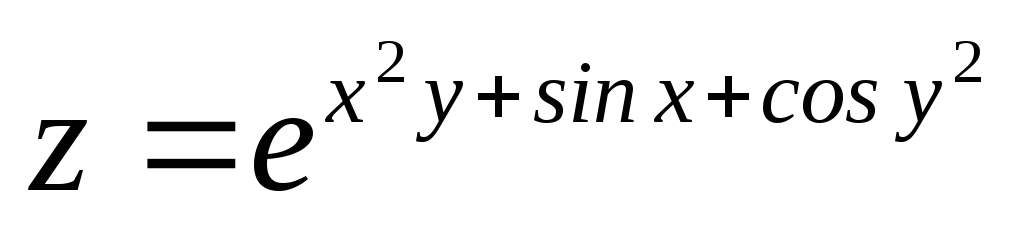 .
.
Имеем:
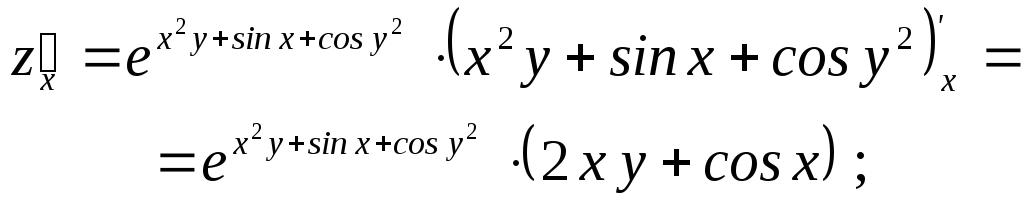
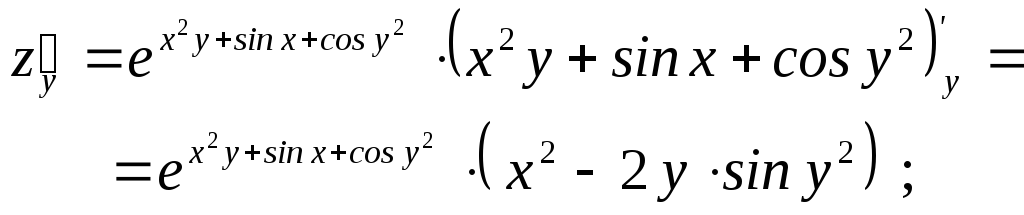
Пример 6 (Нахождение частных производных 2-го
порядка).
Найдем
![]() ,
,![]() ,
,![]() ,
,![]() для
функции
для
функции![]() .
.
Имеем:
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() .
.
