
- •Министерство образования и науки Российской Федерации
- •Введение измерение физических величин и расчет погрешностей измерений
- •Погрешности измерений
- •Расчет погрешности измерений
- •Случайные погрешности при прямых измерениях
- •Приборные погрешности при прямых измерениях
- •Вычисление погрешностей при косвенных измерениях
- •Правила округления
- •Графическое представление результатов
- •Лабораторная работа № 2.
- •Лабораторная работа № 3 измерение сопротивлений
- •Лабораторная работа № 4.
- •Определение емкости конденсатора баллистическим методом
- •Лабораторная работа № 6 изучение зависимости мощности источника тока от сопротивления нагрузки
- •Лабораторная работа № 13 изучение последовательной цепи переменного тока
- •Лабораторная работа № 14 изучение вольтамперной характеристики полупроводникового диода
- •Лабораторная работа № 3-о
- •Определение длины волны с помощью дифракционной решетки
- •Цель работы. Определение длин волн линий спектра ртутной лампы.
- •Лабораторная работа № 4-о
- •Определение фокусных расстояний линз
- •Цель работы: Определение фокусного расстояния собирающей линзы.
- •Контрольные вопросы.
- •Литература.
- •Оглавление
Расчет погрешности измерений
Измерения называются прямыми, если значения величин определяются приборами непосредственно (например, измерение длины линейкой, определение времени секундомером и т. д.). Измерения называютсякосвенными, если значение измеряемой величины определяется посредством прямых измерений других величин, которые связаны с измеряемой определенной зависимостью.
Случайные погрешности при прямых измерениях
Абсолютная и относительная погрешность. Пусть проведеноNизмерений одной и той же величиныxв отсутствии систематической погрешности. Отдельные результаты измерений имеют вид:x1,x2, …,xN. В качестве наилучшего выбирается среднее значение измеренной величины:
![]() .
(1)
.
(1)
Абсолютной погрешностьюединичного измерения называется разность вида:
![]() .
.
Среднее значение абсолютной погрешности Nединичных измерений:
![]() (2)
(2)
называется средней абсолютной погрешностью.
Относительной погрешностью называется отношение средней абсолютной погрешности к среднему значению измеряемой величины:
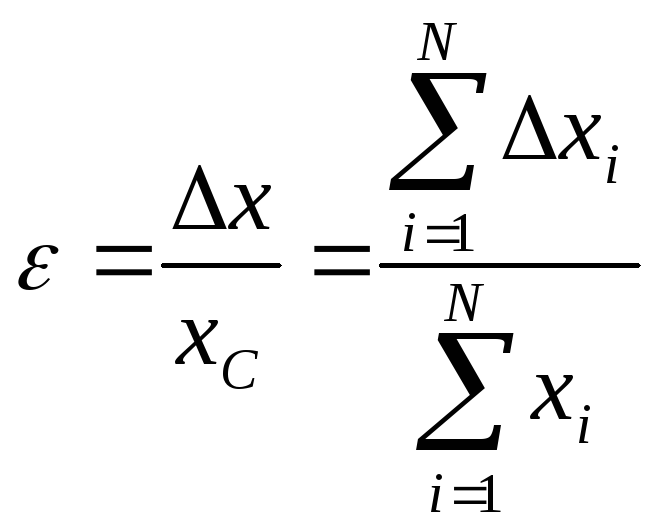 .
(3)
.
(3)
Приборные погрешности при прямых измерениях
Если нет особых указаний, погрешность прибора равна половине его цены деления (линейка, мензурка).
Погрешность приборов, снабженных нониусом, равна цене деления нониуса (микрометр – 0,01 мм, штангенциркуль – 0,1 мм).
Погрешность табличных величин равна половине единицы последнего разряда (пять единиц следующего порядка за последней значащей цифрой).
Погрешность электроизмерительных приборов вычисляется согласно классу точности С, указанному на шкале прибора:
Например:
![]() и
и![]() ,
,
где Umax и Imax – предел измерения прибора.
Погрешность приборов с цифровой индикацией равна единице последнего разряда индикации.
После оценки случайной и приборной погрешностей в расчет принимается та, значение которой больше.
Вычисление погрешностей при косвенных измерениях
Большинство измерений являются косвенными. В этом случае искомая величина Х является функцией нескольких переменных а, b, c…, значения которых можно найти прямыми измерениями: Х = f(a,b,c…).
Среднее арифметическое результата косвенных измерений будет равно:
X = f(a,b,c…).
Одним
из способов вычисления погрешности
является способ дифференцирования
натурального логарифма функции Х =
f(a,b,c…).
Если, например, искомая величина Х
определяется соотношением Х =
![]() ,
то после логарифмирования получаем:lnX
= lna
+ lnb
+ ln(c+d).
,
то после логарифмирования получаем:lnX
= lna
+ lnb
+ ln(c+d).
Дифференциал этого выражения имеет вид:
![]() .
.
Применительно к вычислению приближенных значений его можно записать для относительной погрешности в виде:
=
![]() .
(4)
.
(4)
Абсолютная погрешность при этом рассчитывается по формуле:
Х = Х(5)
Таким образом, расчет погрешностей и вычисление результата при косвенных измерениях производят в следующем порядке:
1) Проводят измерения всех величин, входящих в исходную формулу для вычисления конечного результата.
2) Вычисляют средние арифметические значения каждой измеряемой величины и их абсолютные погрешности.
3) Подставляют в исходную формулу средние значения всех измеренных величин и вычисляют среднее значение искомой величины:
X = f(a,b,c…).
4) Логарифмируют исходную формулу Х = f(a,b,c…) и записывают выражение для относительной погрешности в виде формулы (4).
5)
Рассчитывают относительную погрешность
=
![]() .
.
6) Рассчитывают абсолютную погрешность результата по формуле (5).
7) Окончательный результат записывают в виде:
-
Х = ХсрХ
= …%
Абсолютные и относительные погрешности простейших функций приведены в таблице:
|
Функция |
Абсолютная погрешность |
Относительная погрешность |
|
a+b |
a+b |
|
|
a-b |
a+b |
|
|
ab |
ab+ba |
|
|
|
|
|
|
|
|
|
|
sin a |
|
|
|
cos a |
|
|

