Розміщення без повторень.

Перевірка лекційного матеріалу (фронтальне опитування)

• Дайте означення упорядкованої множини

• Сформулюйте правило суми

• Сформулюйте правило добутку

• Яка функція називається факторіалом

• Дайте означення розміщення з елементів по

• Запишіть формули за якими знаходиться

• Дайте означення перестановки з 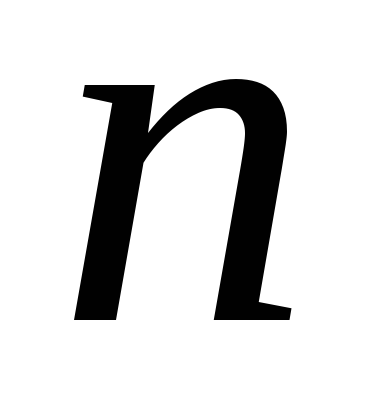елементів

Задача 1. Розклад на день містить 5 уроків. Визначити кількість можливих розкладів при виборі зі 11 дисциплін, при умові, що жоден предмет не стоїть у розкладі двічі на день.

Розв’язання. Зрозуміло, що таких розкладів буде

.

Задача 2. Комісія складається з голови, його заступника і ще п'яти чоловік. Скількома способами 7 членів комісії можуть розподілити між собою обов'язки ?

Розв’язання. Очевидно, що на кількість способів впливає лише вибір голови та його заступника, бо інші члени комісії "визначаються" автоматично. Отже, всього розподіл обов'язків може відбутися способами.

Задача 3. Із групи в 15 чоловік вибирають чотирьох учас­ників естафети 800x400x200x100 м. Скількома способами можна розставити спортсменів на етапах такої естафети ?

Розв’язання. способами.

Задача 4. Скільки різних правильних дробів можна скласти з чисел 3,5,7,11,13,17,19,23 так, щоб в кожний дріб входило два числа ?

Розв’язання. Дробів, у яких чисельник не дорівнює знаменнику, можна скласти штук, але лише половина з них правильні. Отже, маємо 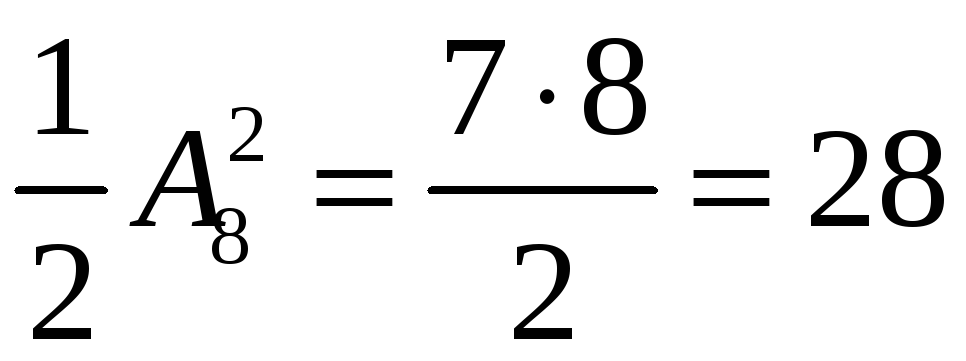дробів.

Задача 5. Скільки можна скласти різних неправильних дробів, чисельниками і знаменниками яких є числа 3,5,7,13,17 ?

Розв’язання. Дробів, у яких чисельник не дорівнює знаменнику, можна скласти штук, але лише половина з них неправильні. До цих дробів треба ще додати дроби, у яких чисельник дорівнює знаменнику, тобто дроби, рівні одиниці; їх 5. Остаточно маємо 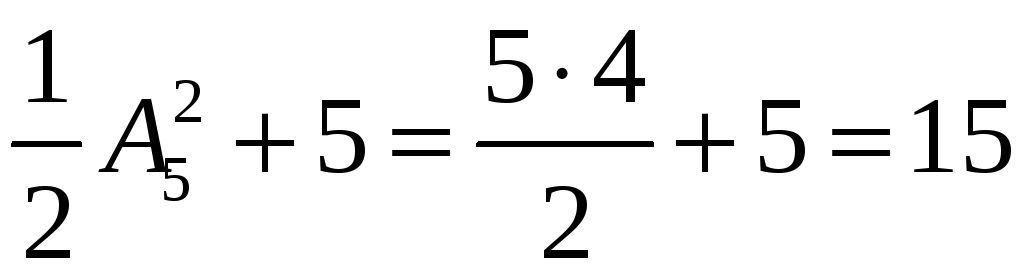дробів.

Задача 6. Скільки різних натуральних чисел можна скласти з цифр 0,1,2,3,4, щоб в кожне таке число кожна з цих цифр входила не більше одного разу ?

Розв’язання. Різних одноцифрових натуральних чисел буде . Число різних двоцифрових виразів з такими умовами дорівнює , а різних двоцифрових чисел буде на менше, а саме: . Розмірковуючи аналогічно, отримаємо, що за такими умовами можна скласти трицифрових чисел, чотирицифрових чисел, п'ятицифрових чисел. Отже, всього можна утворити чисел.

Задача 7. Скільки різних чотирицифрових чисел можна скласти з цифр 0,1,2,3,4,5,6,7 так, щоб у кожному числі була цифра 1 ? (Цифри в числі не повинні повторюватися).

Розв’язання. Чисел, у яких одиниця стоїть на першому місці, буде . Чисел, у яких одиниця стоїть на другому (третьому, четвертому) місці, теж було б по , якби в даний набір цифр не входив би нуль. Тому слід виключити ті числа, де нуль стоїть на першому місці, а їх по . Остаточно маємо: чисел.

Перестановки без повторень.

Задача 8. Учасники шахового турніру грають в залі, де є 8 столів. Скількома способами можна розмістити шахістів, якщо учасники всіх партій відомі?

Розв’язання. За умовою пари шахістів відомі. Тому досить розподілити столи між 8 парами, а це можна зробити способами.

Задача 9. Скільки різних п’ятицифрових чисел можна скласти з цифр 0,1,2,3,4 , якщо в кожному числі жодна з цифр не повторюється ?

Розв’язання. З даних п'яти цифр можна утворити п'ятицифрових виразів. Але оскільки серед цифр є нуль, то треба виключити числа, що починаються з нього; тобто чисел. Отже, таким чином можна отримати чисел.

Задача 10. Скількома способами можна розставити 4 книжки з алгебри і 3 з геометрії, щоб усі книжки з геометрії стояли поруч?

Розв’язання. Об'єднаємо книжки з геометрії умовно в одну. Тоді маємо 5 книг і розстановок. Книги з геометрії можна розставляти "всередині" нової книги способами. Всього, за правилом добутку, способів.

Задача 11. Скільки п'ятицифрових чисел можна утворити з цифр 1,2,3,4,5 (без повторення) так, щоб парні цифри не стояли поруч ?

Розв’язання. З цих цифр будується п’ятицифрових чисел. Серед них є і такі, що містять 2 і 4 поруч; їх буде . Остаточно маємо числа.

Додаткові завдання.

1. В класі 30 учнів. Скількома способами можна серед них вибрати старосту та його заступника ?

2. Шаховий турнір, в якому беруть участь 18 шахістів, проводиться в один круг. Скільки буде зіграно партій в цьому турнірі ?

3. З команди, в якій 10 плавців, вибирається четвірка, що приймає участь в естафеті комплексним плаванням (тобто кожний пливе своїм стилем). Скількома способами можна вибрати цю естафетну четвірку ?

4. Три гімнастки України приймають участь у чемпіонаті світу разом ще з 33 спортсменками інших країн. Скількома способами можуть бути розподілені місця, що посіли члени команди України, при умові, що жодне місце не може бути поділено?

5. Чотири біатлоністи з України приймали участь у чемпіонаті світу. Відомо, що жоден з них не посів місце, нижче п'ятнадцятого. Скількома способами могли бути розподілені місця, що посіли представники України, при умові, що жодне місце не було поділено ?

6. Скільки різних трицифрових натуральних чисел можна скласти з цифр 1,2,3,4,5 при умові, що в кожне число входить кожна з цих цифр не більше одного разу ?

7. Скільки різних правильних нескоротних дробів можна скласти з чисел 1,2,3,4,5,6,7,8 так, щоб в кожний дріб входило два числа ?

8. П'ять викладачів мають розподілити між собою п'ять глав книги так, що кожен викладач пише одну главу. Скільки є способів для цього ?

9. Скільки різних чотирицифрових чисел можна скласти з цифр 1,2,3,4, якщо кожну з них використовувати лише один раз ?

10. Скількома способами можна розставити 5 книжок з математики і 3 з фізики, щоб усі книжки з одного предмету стояли поруч ?

11. В чемпіонаті України з футболу грає 18 команд. Скількома способами можуть розподілитись місця, зайняті командами, якщо відомо, що команди "Динамо", "Дніпро", "Шахтар", "Чорноморець" і "Таврія" займуть перші п'ять місць ?

12. Скількома способами можна вишикувати в одну шеренгу гравців двох футбольних команд (по 11 чоловік) так, щоб при цьому два футболісти однієї команди не стояли поруч ?