12. 2. Агрегатные индексы физического объёма, цен и себестоимости

На изменение стоимости оказывает влияние, как изменение цен, так и изменение объёма выпуска продукции.

Чтобы определить влияние только объёма продукции на изменение стоимости, строят агрегатный индекс физического объёма.

Для этого изменяют объём продукции базисный на отчётный, а цена за единицу продукции не изменяется, а фиксируется на уровне базисного периода и поэтому не влияет на индекс.

-агрегатный (общий) индекс физического объёма (индекс количественного показателя), где

объём - индексируемая величина;

цена - вес индекса, соизмеритель.

Чтобы определить влияние только изменения цен, строят агрегатный индекс цен: в нём изменяется цена, а объём фиксируется на уровне текущего периода, т.е. не влияет на индекс.

-агрегатный (общий) индекс цен (индекс качественного показателя), где

цена – индексируемая величина;

объём - вес индекса, соизмеритель.

Между агрегатными индексами существует взаимосвязь - индекс стоимости равен произведению индекса физического объёма на индекс цен

Наличие этой взаимосвязи позволяет проследить и проанализировать связь между экономическими явлениями.

Формулы агрегатных индексов позволяют разложить общий абсолютный прирост стоимости пофакторам, т.е.:

где pq - абсолютный прирост стоимости продукции (общий);

абсолютный прирост стоимости продукции, обусловленный изменением физического объёма продукции;

pq ( р) - абсолютный прирост стоимости продукции, обусловленный изменением уровня цен на продукцию.

Каждая из названных величин абсолютного прироста рассчитывается как разность числителя и знаменателя соответствующего агрегатного индекса:

Например: определить общие индекс (I p_q) и агрегатные (I _q и I _р)

Вид продукции	Цена изделия (тыс.руб).		Выпуск продукции (шт).
	1кв.р0	2кв. р1	lкв. q0	2кв. q1
А В	20 50	19,5 52	100 30	105 27

1. Определим общий индекс стоимости:

Таким образом стоимость продукции уменьшилась на 1,39%, а экономический эффект составил 48,5 тыс.руб.

2. Определим общий индекс цены:

Таким образом, общий индекс цены возрос на 0,04%, а абсолютный прирост стоимости, вызванный увеличением цен равен 1,5 тыс. руб.

3. Определим общий индекс физического объёма:

Таким образом, на 1,43% стоимость снизилась из-за уменьшения выпуска

продукции, что в абсолютном выражении равно 50 тыс. руб.

Индивидуальный индекс себестоимости

- характеризует изменение себестоимости отдельных видов продукции.

Сводный индекс себестоимости рассчитывается для определения себестоимости нескольких видов продукции, выпускаемых предприятием.

При этом себестоимость взвешивается по объему производства отдельных видов продукции текущего периода.

- показывает сумму экономии предприятия от снижения себестоимости.

Сводный индекс физического объема, взвешенный по себестоимости

Сводный индекс затрат на производство

=

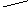
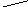3. Средние арифметические и средние гармонические индексы

На практике очень часто не известны абсолютные значения индексируемых величин, а имеются данные об их относительном изменении. В таких случаях вместо агрегатных индексов вычисляются средние из индивидуальных индексов, которые в свою очередь делятся на:

- средние арифметические

- средние гармонические

Применение той или иной формулы индекса зависит от имеющейся в нашем распоряжении информации

-средний арифметический индекс физического объема;

рассмотрим вывод:

т.к.

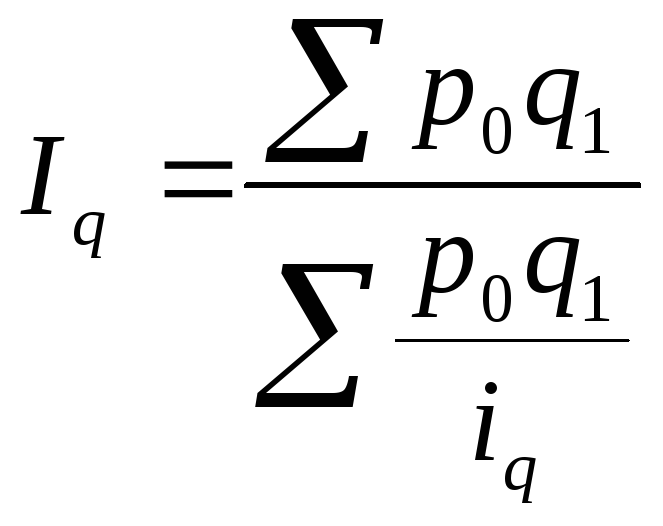- средний гармонический индекс физического объёма;

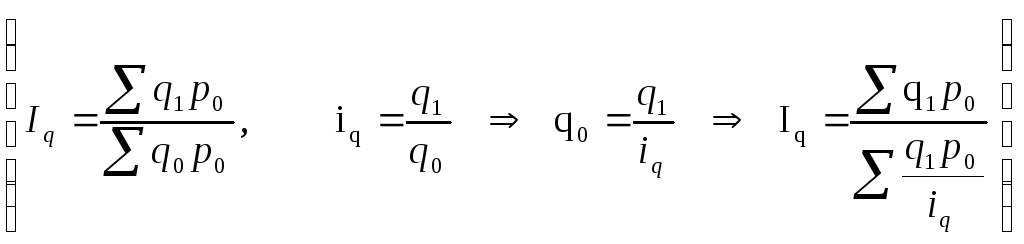
- средний арифметический индекс цены;

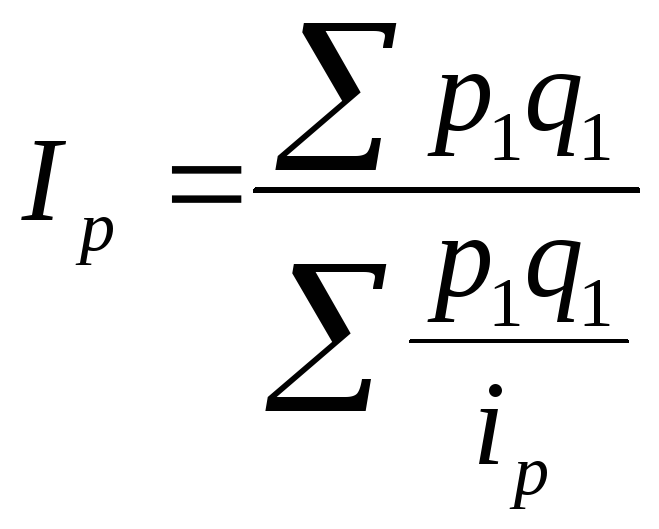
- средний гармонический индекс цены.

(Для индексов цены вывод аналогичен).

Задача 1.

Имеются следующие данные о выпуске продукции мебельной фабрики:

Наименование изделий	Изменение выпуска в мае по сравнению с апрелем, %	Товарооборот продукции в апреле, млн. руб.
Столы Диваны Стулья	+12 +10 +15	20 50 30

Определить увеличение выпуска всей продукции в мае по сравнению с апрелем (в %), т.е. рассчитать общий индекс физического объема.

Решение.

Общий индекс физического объема может быть рассчитан как средний арифметический:

или 111,9%

Задача 2.

По данным таблицы получите сводную оценку изменения цен.

Реализация овощной продукции

Товар	Реализация в текущем периоде, руб.	Изменение цен в текущем периоде по сравнению с базисным, %	Расчетные графы
Морковь Свекла Лук	23000 21000 29000	+4,0 +2,3 – 0,8	1,040 1,023 0,992	22115 20528 29234
Итого	73000	х	х	71877

Решение.

Вычислим средний гармонический индекс цен:

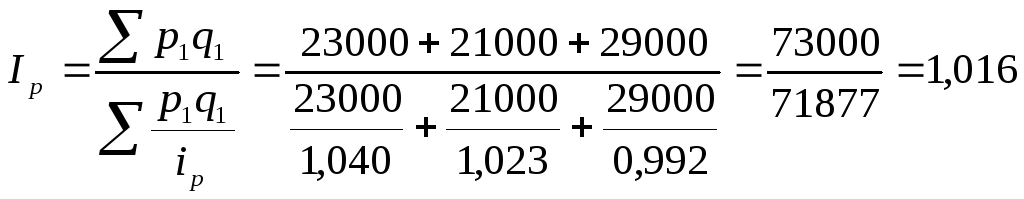или 101,6%.

Таким образом, цены по данной товарной группе в текущем периоде по сравнению с базисным периодом, в среднем выросли на 1,6%.