
- •Учебное пособие
- •Содержание
- •Введение
- •Тема 1. Предмет и метод статистики
- •Тема 2. Статистические наблюдения
- •2.1. Понятие о статистической информации
- •2.2. Основные организационные формы статистического наблюдения.
- •2.3. Ошибки статистического наблюдения
- •Тема 3. Сводка и группровка статистических данных
- •Тема 4. Выборочное наблюдение
- •Тема 5. Способы наглядного представления статистических данных
- •5. 2. Статистические графики
- •Тема 6. Абсолютные и относителбные величины в статистике
- •6.1. Статистические показатели, их виды
- •6. 3. Относительные величины
- •Тема 7. Средние величины
- •Тема 8. Мода, медиана, квартили
- •8.1. Мода
- •8.2. Медиана
- •8.3. Квартили
- •Тема 9. Ряды динамики и ряды распределения
- •9. 1. Ряды динамики
- •9.2. Приемы обработки и анализа рядов динамики
- •9.3. Выявление сезонных колебаний
- •Тема 10. Средние характеристики рядов динамики
- •Тема 11. Показатели вариации
- •9.1. Абсолютные показатели вариации
- •9.2. Относительные показатели вариации
- •2. Относительное линейное отклонение:
- •3. Коэффициент вариации:
- •Тема 12. Индексы
- •12.1. Понятие об индексах
- •12. 2. Агрегатные индексы физического объёма, цен и себестоимости
- •4. Базисные и цепные индексы, их взаимосвязь
- •12.5. Индексы средних величин
- •Тема 13. Статистическое изучение связей между явлениями
- •13.1. Типы связей между явлениями, их характеристика
- •13.2. Методы выявления наличия корреляционной связи между двумя признаками
- •13.3. Измерение степени тесноты корреляционной связи между двумя признаками
- •13.4. Уравнения регрессии, их виды
- •13.5. Корреляционно-регрессивные модели (крм),
Тема 4. Выборочное наблюдение
Понятие о выборочном наблюдении
Выборочное наблюдение представляет собой один из наиболее широко применяемых видов сплошного наблюдения.
Выборочное наблюдение – это метод статистического исследования, при котором характеристика всей совокупности фактов (генеральной совокупности) дается по некоторой ее части (выборочной совокупности).
В последние годы выборочное наблюдение широко применяется в работе органов статистики, так как это позволяет:
− сэкономить затраты средств и труда на обработку информации;
− сократить ошибки регистрации на этапе сбора данных;
− повысить оперативность получения сведений.
В отличие от других методов несплошного наблюдения (монографического наблюдения, метода основного массива) выборочное наблюдения имеет важную особенность – возможность попадания в выборочную совокупность равна для всех единиц генеральной совокупности.
Это предупреждает появление тенденциозных ошибок при формировании выборки.
Виды выборочного наблюдения
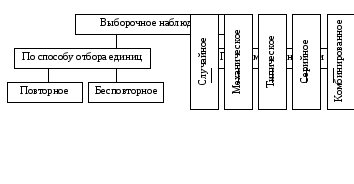
Рис.1. Классификация выборочного наблюдения
В зависимости от способа отбора единиц различают:
− повторную выборку – после отбора, какой-то единицы, она снова возвращается в совокупность и может быть снова набрана, т.е. вероятность попадания каждой отдельной единицы в выборочную совокупность остается постоянной;
− бесповторную выборку – отобранная единица не возвращается обратно и возможность попадания у оставшихся единиц в выборочную совокупность постоянно возрастает.
По форме организации способа отбора выборочное наблюдение может быть:
случайным – случайный отбор;
механическим – отбор единиц в выборочную совокупность из генеральной производится через равные интервалы (группы);
типическим – в выборочной совокупности более равномерно представлены различные типы (части) генеральной совокупности;
серийным – отбираются серии единиц, которые подвергаются сплошному исследованию;
комбинированным – комбинация нескольких форм организации выборочного наблюдения.
Ошибки выборочного наблюдения
Между характеристиками выборочной и генеральной совокупности, как правило, существует расхождение, которое называется ошибкой.
Ошибки выборочного наблюдения могут быть двух видов:
− ошибки регистрации – свойственны любому наблюдению, вызваны несовершенством измерительных приборов, недостаточной квалификацией работников и т.п.;
− ошибки репрезентативности (представительности) присущи только несплошным наблюдениям, возникают из-за того, что выборочная совокупность не точно характеризует генеральную.
Ошибка выборки зависит от следующих факторов:
− степени вариации изучаемого признака;
− численности выборки;
− метода отбора единиц в выборочную совокупность;
− принятого уровня достоверности результатов исследования.
В математической статистике доказывается, что значение средней ошибки повторной выборки равно:
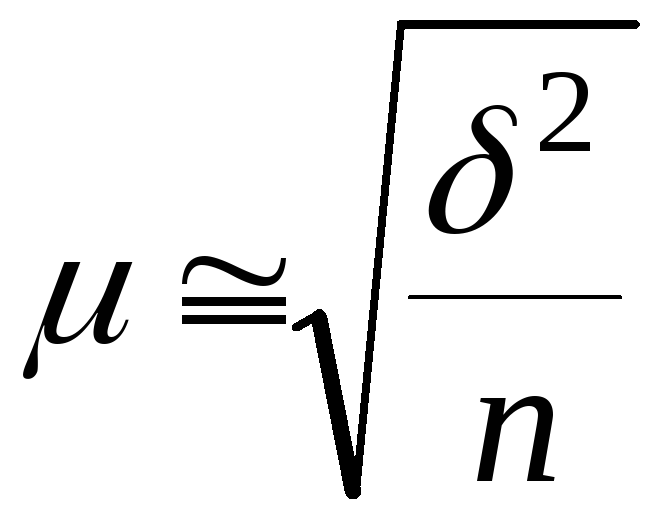 −средняя,
−средняя,
 −среднее
квадратическое отклонение выборочное
или генеральное,
−среднее
квадратическое отклонение выборочное
или генеральное,
где µ − ошибка выборки;
δ2 − дисперсия (средний квадрат отклонений);
n − объем выборки (число обследованных единиц).
При бесповторном отборе формула средней ошибки выборки принимает вид:
 ,
где
,
где
N – объем генеральной совокупности.
Предельная ошибка
выборки
![]() ,
гдеt
– коэффициент доверия. Определяется
по справочным таблицам в зависимости
от уровня вероятности.
,
гдеt
– коэффициент доверия. Определяется
по справочным таблицам в зависимости
от уровня вероятности.
В целом ряде случаев
средние и относительные величины для
какой-либо совокупности рассчитываются
на основе данных выборочного наблюдения,
суть которого заключается в том, что из
генеральной совокупности, наудачу,
чисто случайно, отбирается n
единиц, составляющих выборочную
совокупность; для отобранных единиц
рассчитываются обобщенные характеристики
(средние или относительные показатели),
а затем результаты выборочного
обследования распространяются на всю
генеральную совокупность. Основной
задачей при этом является определение
ошибок выборки, т.е. возможных расхождений
между выборочной средней (![]() )
и генеральной (
)
и генеральной (![]() )
или выборочной долей единиц (w),
обладающих изучаемым признаком, и
генеральной долей (p).
)
или выборочной долей единиц (w),
обладающих изучаемым признаком, и
генеральной долей (p).
Различают среднюю и предельную ошибки выборки.
Средняя ошибка выборки (µ) характеризует среднюю величину возможных расхождений выборочной и генеральной средней (или доли) и представляет собой по форме и содержанию среднее квадратическое отклонение возможных значений выборочной средней от генеральной.
В математической
статистике доказывается, что
![]() - дисперсия возможных значений выборочной
средней – вn
раз меньше дисперсии изучаемого признака
и генеральной совокупности, т.е.
- дисперсия возможных значений выборочной
средней – вn
раз меньше дисперсии изучаемого признака
и генеральной совокупности, т.е.
 .
.
Исходя из этого средняя ошибка выборочной средней при повторном отборе определяется по формуле:
 ,
,
где
![]() - дисперсия изучаемого показателя в
генеральной совокупности (т.к. дисперсия
изучаемого показателя в генеральной
совокупности неизвестна, то фактически
в формулу подставляется дисперсия
выборочная, которая при большом числе
наблюдений близка к генеральной), аn
– объем (численность) выборки.
- дисперсия изучаемого показателя в
генеральной совокупности (т.к. дисперсия
изучаемого показателя в генеральной
совокупности неизвестна, то фактически
в формулу подставляется дисперсия
выборочная, которая при большом числе
наблюдений близка к генеральной), аn
– объем (численность) выборки.
Как видно из
формулы, средняя ошибка выборки (µ)
при повторном отборе зависит от показателя
вариации (![]() )
и от объема выборки (n).
)
и от объема выборки (n).
Средняя ошибка выборочной доли определяется по формуле:
 ,
где w
– выборочная доля единиц, обладающих
изучаемым признаком, а w(1
− w)
– дисперсия доли (альтернативного
признака).
,
где w
– выборочная доля единиц, обладающих
изучаемым признаком, а w(1
− w)
– дисперсия доли (альтернативного
признака).
При бесповторном
отборе в формулах под знаком радикала
появляется множитель
![]() ,
гдеN
–численность генеральной совокупности.
,
гдеN
–численность генеральной совокупности.
Говоря об ошибках
выборки, следует иметь в виду, что в
каждой конкретной выборке разность
![]() может быть меньше, больше или равнаµ.
И вероятность каждой такой ошибки
различна.
может быть меньше, больше или равнаµ.
И вероятность каждой такой ошибки
различна.
Отклонение выборочной характеристики от генеральной называется предельной ошибкой выборки.
Предельная ошибка
выборки, обозначаемая через
![]() ,
рассчитывается как
,
рассчитывается как
![]() ,
,
где µ − средняя ошибка выборки,
t – коэффициент доверия.
При бесповторной выборке формула ошибки выборки имеет вид:
 ,
,
где δ2 – межсерийная дисперсия;
s – число отобранных серий;
S – число серий в генеральной совокупности.
Все рассмотренные выше формулы используются при так называемой большой выборке.
Если n < 20 (у некоторых авторов n <30), то выборка именуется малой и при расчете ошибок выборки необходимо учитывать следующие моменты. Во-первых, в формуле средней ошибки в знаменателе принимается n – 1, т.е.
 .
.
И, во-вторых, при
нахождении вероятности допуска той или
иной ошибки или определении доверительных
интервалов исследуемого показателя в
генеральной совокупности пользуются
таблицами вероятность Стьюдента, где
![]() определяется в зависимости от объема
выборки иt.
определяется в зависимости от объема
выборки иt.
Формулы предельной ошибки выборки позволяют решить следующие три задачи:
Определить доверительные пределы:
для генеральной средней
![]() ;
;
для доли
![]() .
.
Определить вероятность допуска той или иной заданной ошибки
 .
.
В этом случае
определяется
 и по таблице (приn>20)
находится вероятность (P).
и по таблице (приn>20)
находится вероятность (P).
3. Определить
необходимую численность выборки (n),
обеспечивающую с определенной вероятностью
заданную точность (![]() ).
).
Формулы для n определяются из соответствующих формул предельной ошибки.
Так, для определения
средней (![]() )
из формулы
)
из формулы приповторном
отборе
имеем:
приповторном
отборе
имеем:
 .
.
Для доли аналогично
из
 получаем:
получаем:
 .
.
При бесповторном
отборе из
 и
и![]() имеем:
имеем:
 −для средней (
−для средней (![]() );
);
![]() −для доля (w).
−для доля (w).
Как видно, в формулах
для определения необходимой численности
выборки, получаемых из формул случайной
ошибки выборки, предполагается
обязательное знание величины дисперсии
признака (![]() )
или [w
(1
– w)].
)
или [w
(1
– w)].
Обычно в этих
формулах используется значение дисперсии
признака в аналогичных предшествующих
исследованиях или же проводится пробное
обследование небольшого числа единиц,
для которых определяется значение
![]() .
В случае изучения доли определенных
единиц в совокупности при отсутствии
каких-либо сведений о дисперсии
принимается максимальное значение [w
(1
– w)],
равное 0,25.
.
В случае изучения доли определенных
единиц в совокупности при отсутствии
каких-либо сведений о дисперсии
принимается максимальное значение [w
(1
– w)],
равное 0,25.
Рассмотрим решение некоторых задач к этой теме с применением формул предельной ошибки выборки.
Задача 1.
Методом собственно случайной выборки обследована жирность молока у 100 коров. По данным выборки средняя жирность молока оказалась равной 3,64%, а дисперсия составила 2,56.
Определить: а) среднюю ошибку выборки; б) с вероятностью, равной 0,954, предельные значения генеральной средней.
Решение.
А. Формула средней
ошибки выборки:
 .
.
По условию n
= 100,
![]() =2,56.
Отсюда
=2,56.
Отсюда![]()
Б. Формула предельной
ошибки выборки:
![]() .
.
По таблице значений
F(t)
при P
= 0,954 находим,
что t
= 2. Отсюда
![]() ,
или
,
или![]() ,
т.е. предельные значения жирности молока
(или доверительный интервал генеральной
средней) определяются как
,
т.е. предельные значения жирности молока
(или доверительный интервал генеральной
средней) определяются как![]() .
.
Задача 2.
На основе выборочного обследования 600 рабочих (n = 600) одной из отраслей промышленности установлено, что удельный вес численности женщин составил 0,4 (w = 0,4).
С какой вероятностью
можно утверждать, что при определении
доли женщин, занятых в отрасли, допущена
ошибка (![]() ),
не превышающая 5% (0,05)?
),
не превышающая 5% (0,05)?
Решение.
Чтобы определить
вероятность допуска той или иной ошибки,
из формулы
![]() находим показательt,
связанный с вероятностью:
находим показательt,
связанный с вероятностью:
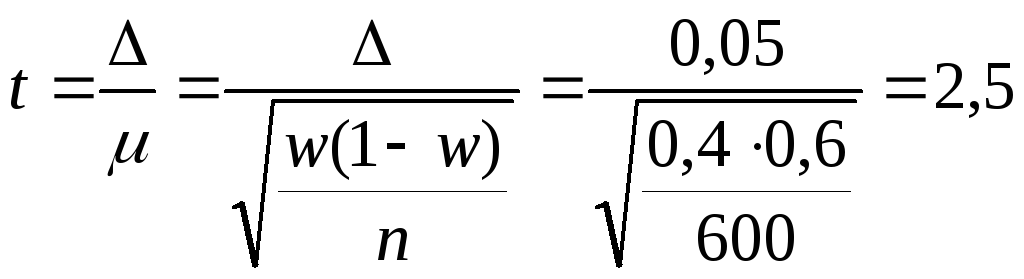
По таблице значений F(t) для t=2,5 находим, что P=0,988, т.е. с вероятностью 0,988 можно утверждать, что при определении доли женщин (0,4) в общем числе рабочих допущена ошибка не более 0,05 (5%).
Задача 3.
Сколько рабочих
завода нужно обследовать в порядке
случайной выборки для определения
средней заработной платы, чтобы с
вероятностью (P),равной
0,954, можно было бы гарантировать ошибку
не более 50 руб.? Предполагаемое среднее
квадратическое отклонение заработной
платы
![]() =200
руб.
=200
руб.
Решение.
Из формулы
![]() находимn:
находимn:
![]() (человека).
(человека).
Контрольные вопросы к теме:
Дайте определение выборочного наблюдения. Для чего в экономике применяют выборочное наблюдение.
Перечислите и охарактеризуйте виды выборочного наблюдения.
Расскажите об ошибках выборочного наблюдения, от каких факторов они зависят.
Расскажите о предельной ошибке выборки, какие задачи позволяют решить формулы предельной ошибки выборки.
