9.1. Абсолютные показатели вариации

Различие индивидуальных значений признака внутри изучаемой совокупности в статистике называется вариацией признака.

Она возникает в результате того, что индивидуальные значения складываются под влиянием разнообразных факторов.

Колеблемость отдельных значений характеризуют показатели вариации.

Показатели вариации могут быть:

− абсолютными;

− относительными.

Абсолютные показатели вариации:

Наиболее простой показатель – размах вариации (R), определяемый как разность между наибольшим (X_max) и наименьшим (X_min) значениями вариантов:

R = X_max − X_min

Рассмотрим колеблемость показателей товарооборота в среднем на одно предприятие для уяснения расчетов показателей вариации.

Группы предприятий по объему товарооборота, млн. руб.	Число предприятий	Расчетные показатели
90-100	28	95	2660	10	280	100	2800	9025	252700
100-110	48	105	5040	0	0	0	0	11025	529200
110-120	20	115	2300	10	200	100	2000	13225	264500
120 -130	4	125	500	20	80	400	1600	15625	62500
ИТОГО	100		10500		560	600	6400		1108900

Средний объем товарооборота на одно предприятие равен:

млн. руб.

Показатель размаха вариации составил: R = 130 – 90 = 40 млн.руб.

Этот показатель улавливает только крайние отклонения и не отражает отклонения всех вариант в ряду. Однако безусловным достоинством этого показателя является простота вычисления.

Чтобы дать обобщающую характеристику распределения отклонений, исчисляют среднее линейное отклонение (),которое учитывает различие всех единиц изучаемой совокупности. Оно определяется как среднее арифметическое из отклонений индивидуальных значений от средней, без учета знака этих отклонений.

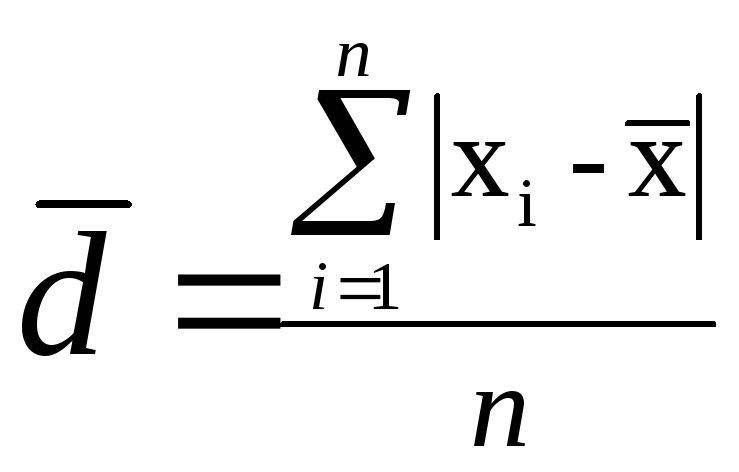, или

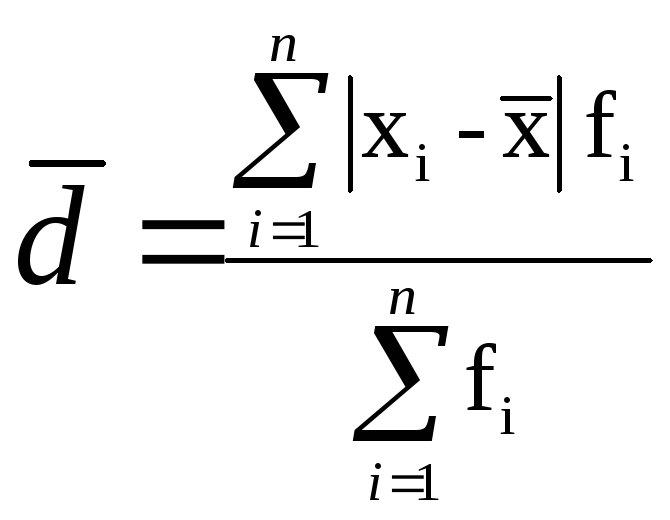
В нашем примере:

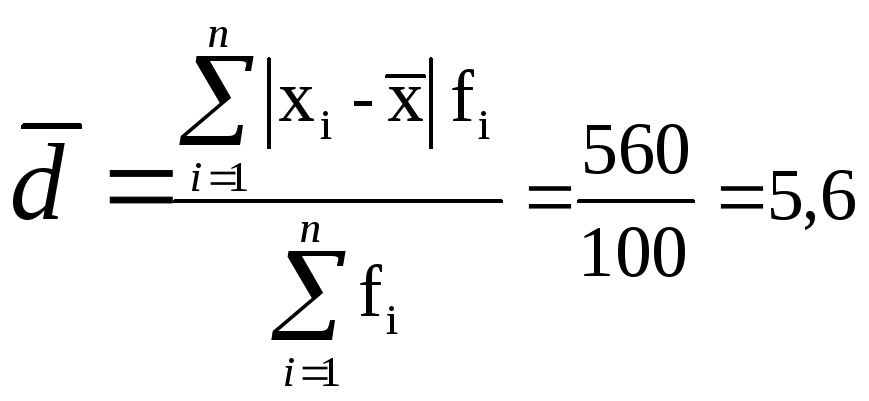млн.руб.

На практике меру вариации более объективно отражает показатель дисперсии (δ²) – средний квадрат отклонений, определяемый, как средняя из отклонений, возведенных в квадрат :

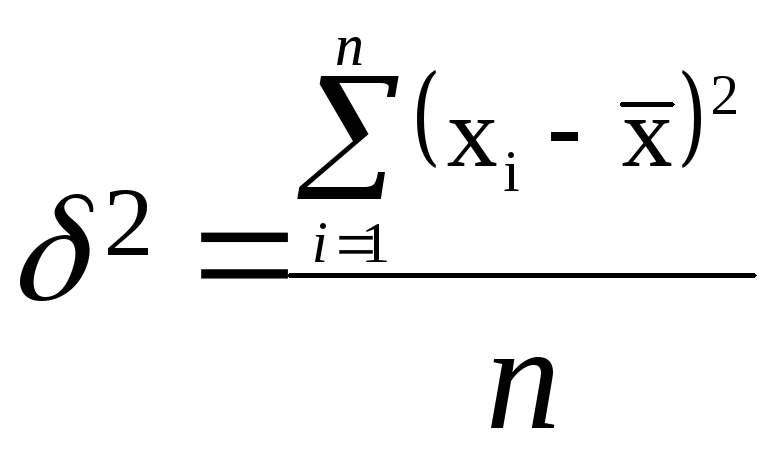
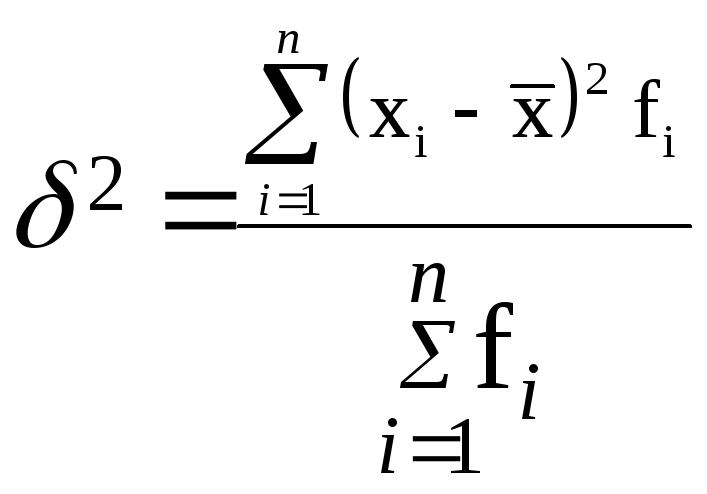
Корень квадратный из дисперсии δ² среднего квадрата отклонений представляет собой среднее квадратическое отклонение:

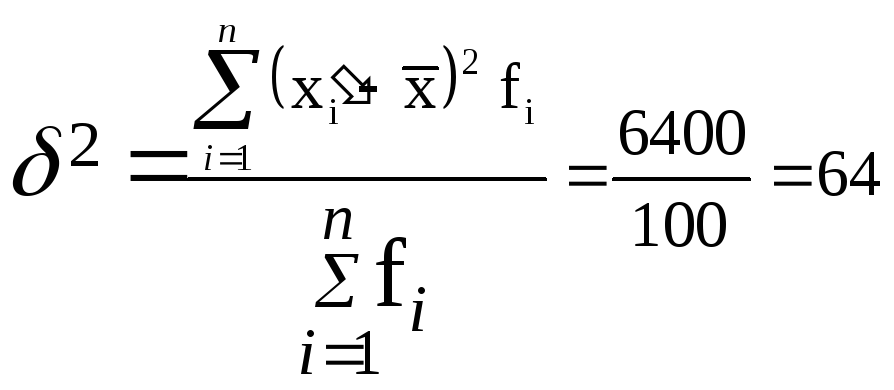
млн. руб.

Среднее квадратическое отклонение является мерилом надежности средней. Чем меньше среднее квадратическое отклонение, тем лучше средняя отражает собой всю представляемую совокупность.

Различают: − дисперсия признака по всей изучаемой совокупности;

−межгрупповая дисперсия – это мера колеблемости частных средних по группами вокруг общей средней;

−внутригрупповая дисперсия – это вариация, обусловленная влиянием прочих факторов.

Общая дисперсия измеряет вариацию признака во всей совокупности под влиянием всех факторов, обусловливающих эту вариацию:

_.

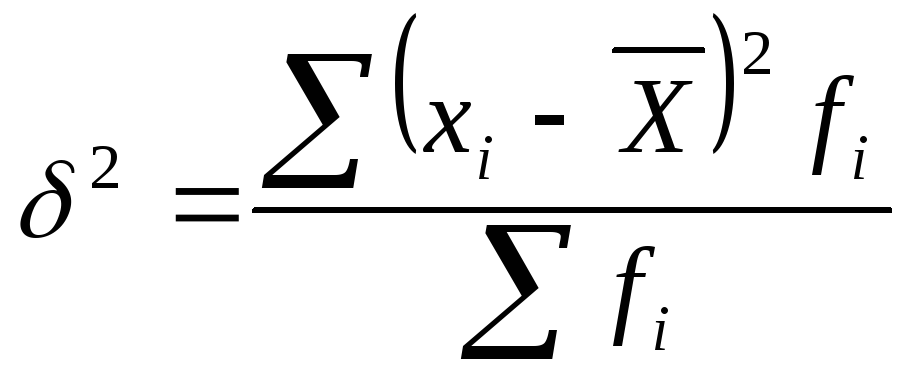Межгрупповая дисперсия характеризует систематическую вариацию, т.е. различия в величине изучаемого признака, возникающие под влиянием признака-фактора, положенного в основание группировки. Она рассчитывается по формуле:

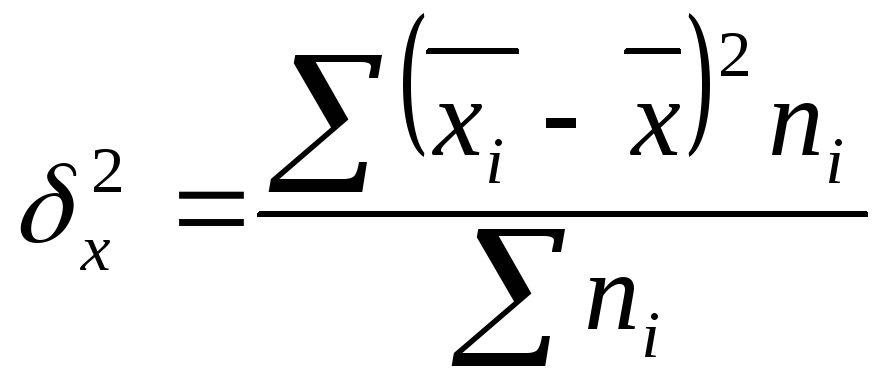, где

x_i и n_i - соответственно средние и численности по отдельным группам.

Внутригрупповая дисперсия отражает случайную вариацию, т.е. часть вариации, происходящую под влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки. Она исчисляется следующим образом:

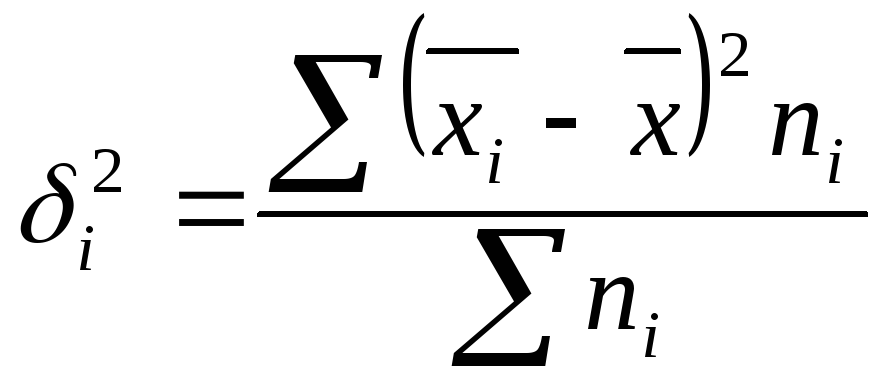
Средняя из внутригрупповых дисперсий

.

Дисперсия обладает рядом свойств, которые позволяют упростить расчеты:

1. Общая дисперсия равна сумме средней из внутригрупповых и межгрупповой дисперсии.

2. Если из всех значений вариант отнять какое-то постоянное число А, то средний квадрат отклонений от этого не изменится.

3. Если все значения вариант разделить на какое-то постоянное число А, то средний квадрат отклонений уменьшится от этого в А раз, а среднее квадратическое отклонение в А раз:

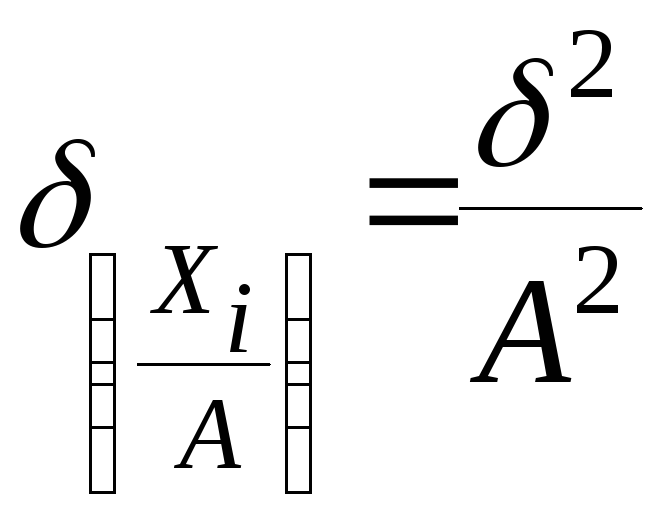
4. Дисперсия равна разности средней из квадратов значений признака и квадрата средней арифметической (способ моментов).

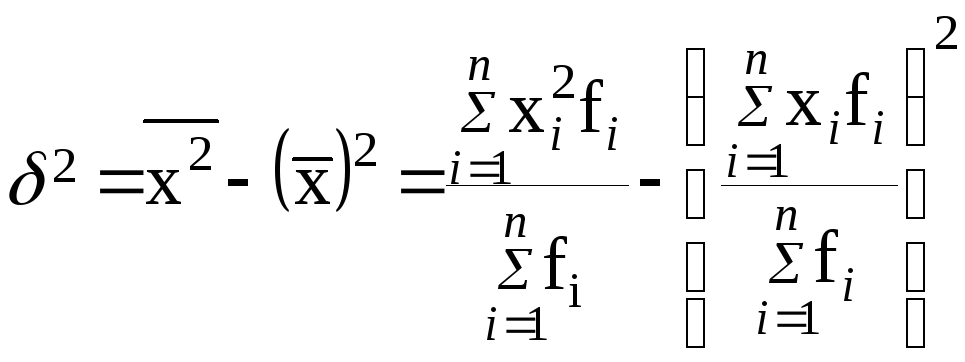или

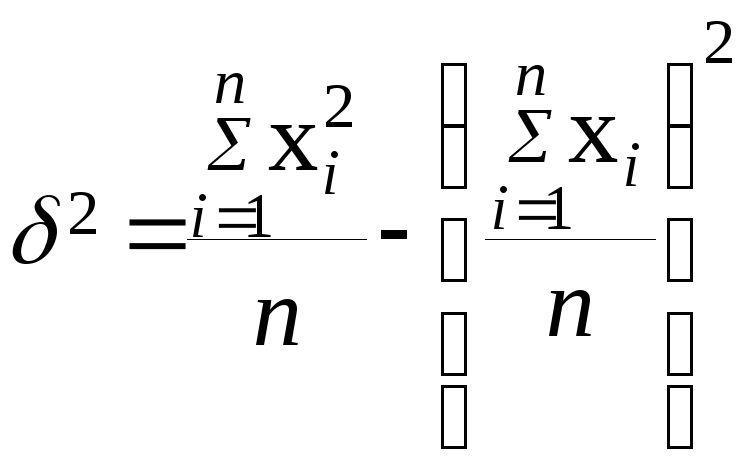
В примере:

Размах вариации, среднее линейное и среднее квадратическое отклонение являются величинами именованными и имеют те же единицы измерения, что и индивидуальные значения признака.