4.3.2. Побудова мережної моделі проекту

Широке росповсюдження у світі одержала система методів керування проектами, відома в Росії за назвою сіткове планування й керування (СПУ). Апарат СНУ призначений для рішення двох основних проблем: формування календарного графіка виконання робіт проекту й прийняття ефективних рішень у процесі його реалізації. Ефект, що досягається при використанні системи СПУ, обумовлений формалізацією структури проекту й кількісним вираженням його параметрів, у першу чергу - тимчасових. Це дозволяє використовувати строгий математичний апарат і засоби обчислювальної техніки для аналізу й синтезу сіткових графіків проектів. Система СПУ — один з найбільш відомих прикладів використання математичного апарата до рішення завдань економіко-управлінського характеру. Вона заснована на графічному поданні комплексу робіт у вигляді мережної моделі проекту, що відображає логічні послідовності й взаємозв'язки між окремими роботами. Для формального відображення мережних моделей застосовується математичний апарат теорії графів.

Основні положення теорії графів. Теорія графів — область дискретної математики, що займається дослідженням і рішенням різноманітних проблем, пов'язаних з об'єктом, названим графом. Перші роботи з теорії графів були виконані в XVIII в. Леонардом Эйлером. Назвемо графом G (N, А) сукупність двох кінцевих нескінченностей: N — нескінченності вершин або вузлів гоафа й А — нескінченності пар цих вершин, названих ребрами графа. З визначення граф може бути заданий аналітично простим перерахуванням елементів обох нескінченностей. Наприклад:

{N}₁ⁿ = 1, 2, 3, 4, 5, 6, де число вершин п = 6;

{N}₁ⁿ = 3-6; 5-1; 2-4; 4-6; 6-5; 1-3; 2-3; 4-1, де число ребер k = 8.

Однак найбільший інтерес представляє другий спосіб його завдання — графічний. Задамо на площині безліч n у виді кружків і безліч А в виді ліній, що з'єднують ці кружки. Тоді той же граф буде мати вигляд, представлений на мал. 4.8. Ребро вважається орієнтованим, якщо порядок проходження вершин у відповідній парі (ij)  A строго заданий. Такі пари називаються дугами графа й зображуються на малюнках стрілками. Граф G (N, А) називається орієнтованим, якщо всі елементи його безлічі А - дуги.

2

2

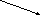
3

3

6

4

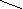
1

6

4

5

5

Рис. 4.8. Граф Рис. 4.9. Орієнтований граф

Якщо вважати заданий вище граф орієнтованим, то його графічне подання буде таким (мал. 4.9). Шлях в орієнтованому графі - це послідовність зчеплених однаково орієнтованих дуг, тобто це така послідовність дуг, у якій кожна вершина, кінцева для попередньої дуги, є початковою для наступної. Цикл у графі - це шлях, що починається й закінчується в одній і тій же вершині. На мал. 4.9 є цикл - 1-3, 3-6, 6-5, 5-1. Вироджений цикл, що складається з однієї дуги (ii)  А називається петлею. Цикл у неорієнтованому графі або цикл, складений з дуг без обліку їхньої орієнтації, називається контуром.

Граф називається зв'язковим, якщо при будь-якій розбивці безлічі його вершин на дві підмножини завжди найдеться хоча б одна дуга, що належить безлічі Л, що зв'язує вершини двох цих підмножин. Заданий нами раніше граф — зв'язний. Граф Н (N, А) є графом-деревом, якщо для нього виконуються два із трьох умов: 1) це зв'язний граф; 2) число його ребер на одиницю менше числа вершин, тобто k = п - 1; 3) він не має контурів. Граф Н (N, А*) є підграфом-деревом графа G (N, А), якщо H(N,A*) — це граф-дерево, побудований на тій же безкінечності вузлів, що й G (N, А), а безкінечності його ребер А* & А. Один з можливих варіантів підграфа-дерева графа, зображеного на мал. 4.8, представлений на мал. 4.10.

/

2

1

3

4

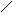
6

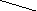
5

Рис. 4.10 Підграф-дерево неорієнтованого графа

Для виконання формальних перетворень і постановки прикладних завдань зручна матрична форма задання графів. Повну інформацію про граф дає матриця суміжності вершин (матриця репрезентативності графа). Це квадратна матриця розмірності п  п, у якій одиниці ставляться на перетинанні i-х рядків й j-х стовпців для всіх дуг (ij)  А. Інші клітки матриці містять нулі. Якщо граф орієнтований, то вершинам i, названим вершинами-предками, відповідають рядки матриці, а вершинам j, названим вершинами-нащадками, - її стовпці. Матриця суміжності вершин графа, заданого за допомогою мал. 4.9, показана в табл. 4.1.

Таблиця 41

Матриця суміжності вершин графа

			Вершини-нащадки
			1		2		3		4		5		6
Вершини-предки	1					1
	2					1		1
	3											1
	4	1										1
	5	1
	6									1

Число одиниць у матриці дорівнює розмірності безкінечності А. Якщо граф не містить петель, то його головна діагональ заповнена нулями Будь-яке ребро неорієнтованого графа можна представити як сукупність двох протилежно спрямованих дуг. Це значить, що матриця репрезентативності неорієнтованого графа включає два повних комплекти одиниць й є симетричною щодо головної діагоналі.

Постановка завдання керування проектом. Нехай даний орієнтований зв'язний граф без циклів G (N, А). Задамо на ньому деяку функцію Т таким чином, що кожній дузі графа (ij)  А поставимо у відповідність деяке ненегативне число t_ij . Назвемо дуги графа роботами, вершини — подіями, а числа t_ij — тривалостями робіт. Робота — це деяка дія, що супроводжується витратами часу, матеріальних, трудових і фінансових ресурсів. Фіктивна робота не вимагає витрат часу або інших ресурсів: t_ij = 0; вона відображає лише логічний взаємозв'язок між подіями (за i треба j). Позначається фіктивна робота, як правило, пунктирною стрілкою. Подія — це проміжний етап виконання комплексу робіт. Подія означає, що всі попередні йому роботи завершені й існують необхідні й достатні умови для початку наступних за ним робіт. З урахуванням уведених визначень граф являє собою мережеву модель комплексу робіт. Таку модель можна віднести до групи однопродуктових моделей, тому що на ній підлягає контролю тільки один параметр - час.

Правила графічного подання мережних моделей. Мережна модель комплексу робіт повинна бути представлена орієнтованим зв'язним графом без циклів. При цьому вона повинна мати тільки одну початкову й одну завершальну подію, тобто один логічний початок й одне завершення проекту. Якщо ця вимога не виконується й виникають так називані глухі кути першого й другого роду, то проблема вирішується введенням фіктивних робіт, як це показано на мал. 4.11

a) б)

Рис. 4.11. Приклад рятування від тупика першого роду в мережі

за допомогою двох фіктивних робіт:

а - технічно невірно виконаний початок мережі; б - початок мережі відповідає вимогам до мережних моделей проектів

Висувається ще одна вимога до мережних моделей. Оскільки одна робота в мережній моделі або дуга в графі зв'язує (представляє) пару суміжних подій або вершин, другий, третьої й т.д. роботи (дуги) між парою тих же вершин бути не може. Однак, слідуючи реальній логіці взаємозв'язку робіт, така конструкція може виникнути. Зняти протиріччя між технікою виконання й логікою мережної моделі допомагають ті ж фіктивні роботи, додатково уведені в мережу (мал. 4.12).

а) б)

Рис. 4.12. Технічно неприпустиме (а) і правильне (б)

графічне подання логічного зв'язку між чотирма роботами