AlgStr / Библиотека / POSIBNIK / Главы для пособия / Матрица

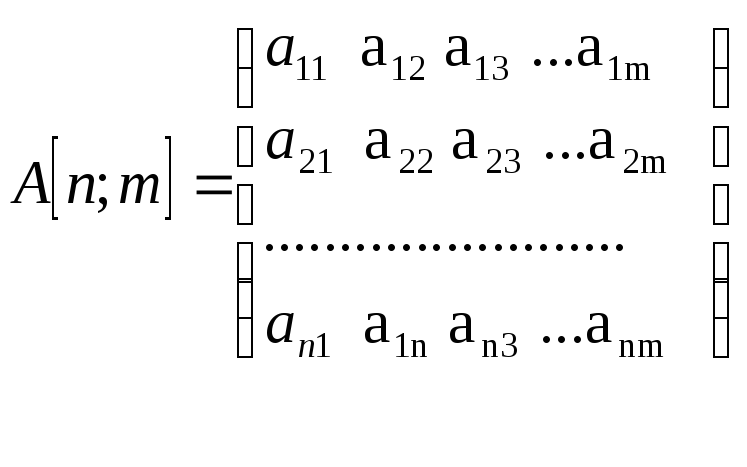
Представление матриц.

Последовательная структура данных - это такая структура, в которой обработка и расположение элементов выполняется последовательно. К данной структуре относятся двумерные массивы (матрицы). Доступ к элементам массива вычисляемый (по индексам).

, , (1)

Сплошное представление массивов в памяти:

Машина представляет в виде линейного способа (последовательно). С помощью формулы приведенного индекса мы можем вычислить месторасположение в линейном виде.

Определение: приведенный индекс – порядковый номер элемента от начала массива представления вектора памяти.

Линейное представление матрицы возможно

• По столбцам;

(2)

Формула приведенного индекса имеет вид:

(3)

Таким образом адрес , где

Существует обратная задача: как по приведенному индексу получить индексы . Для нахождения приведенный индекс делим нацело на и к результату прибавляем 1.

• По строкам;

(4)

Формула приведенного индекса имеет вид:

(5)

Аналогично линейному представлению по столбцам определяем индексы .

Представление разреженных матриц.

Определение: Разреженная матрица –матрица, в которой количество не нулевых элементов менше нулевых.

Все представления, в том числе и представление разреженных матриц состоит из дескриптора и тела (рис.1).

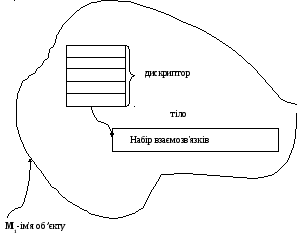
Рис.1 Представлення об’єкту.

Дискриптор содержит общие свойства и дополнительные сведения для оптимальной реализации объекта.

Например: необходимо описать объект- группа студентов. В качестве дискриптора может выступать: шифр группы, куратор.Обычно дескриптор – это запись, которая содержит связь с телом.

Существует два способа представления тела:

• Ограниченное (на базе массива);

• Неограниченное (на базе списка).

Зачастую в качестве тела выступают ограниченное представление.

Рассморим представление данных.

Існує два способи представлення даних:

• За допомогою масиву;

• За допомогою списку.

Виды представления разреженных матриц:

А) Нижняя треугольная матрица

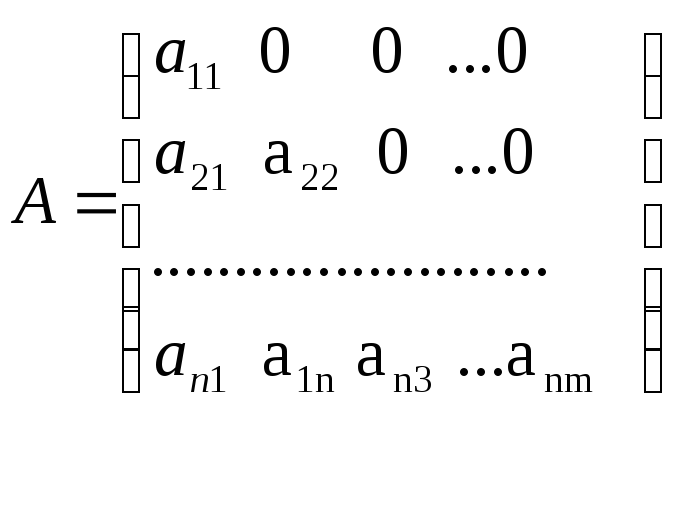
Для представлення нижньої треугольної матриці необхідно представити її у

лінійному вигляді. Нехай тіло – вектор не нульових елементів на та нижче головної діагоналі.

Тоді представлення матриці має вигляд:

Функция абстракции есть:

a₁₁

a₂₁ a₂₂

A: rep  a₃₁ a₃₂ a₃₃

. . .

a_n1 a_n2 a_n3 . . . a_nn

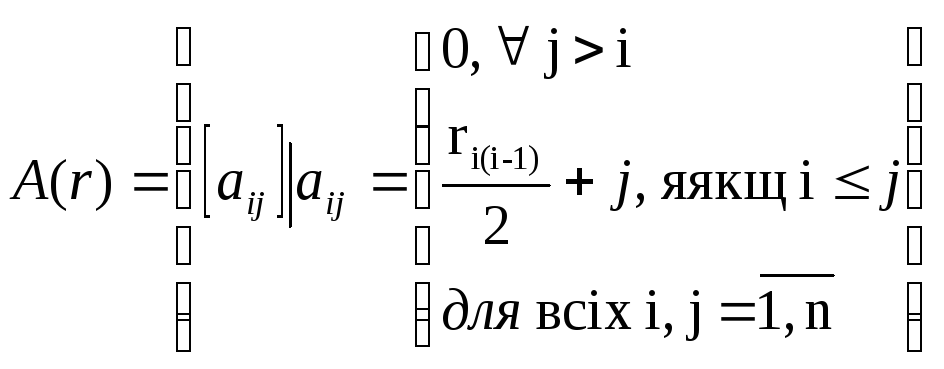
Наступним кроком реалізації є необхідність системи типів. Наприклад: зробимо це за допомогою Turbo Pascal.

Type

Intarray=array[1..65520div sizeof(integer)] of integer;

TMATR=record

n: word;

tbody:^intarray;

end;

PMATR= ^TMATR;

Наступним кроком є опис інтерфейсу типу.

Запишемо операції для роботи з матрицею.

Function Create (n:word):PMATR; // створення матриці

Function Getel (M:PMATR;i,j:word):integer; // отримання елементу матриці

Procedure Destroy(var M: PMATR)//знищення матриці

Зауваження: функція Create повинна працювати за максимумом тобто 65520div sizeof(integer).

Всі ці пункти повинні бути відображені в окремому модулі роботи з матрицею.

Б) Разреженные матрицы:

Способ 1. Упакованный способ хранения запоминаются только ненулевые элементы

i j a_ij

Если  - число ненулевых элементов, то необходимо 3 ячеек. Ясно, что 3 << n² , чтобы оправдать затраты на хранение индексов. При хранении в упакованной форме должна быть каким-то образом предусмотрена возможность добавления новых ненулевых элементов в различные столбцы (или строки) матрицы A.

1. Использование связанных списков.

Каждому элементу a_ij  0 соответствует в памяти запись. Записи j-ого столбца матрицы. Каждая запись будет представлять собой упорядоченную тройку

i a p , где

i – номер строки;

a – значение элемента матрицы;

p – указатель на следующий ненулевой элемент.

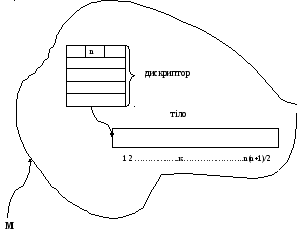
Представление такой матрицы будет состоять из массива голов списков ненулевых элементов по столбцам и списка троек <i, a, p> для каждого ненулевого элемента столбца.

Эту схему можно использовать в перевернутом виде, т.е. по строкам. Тогда массив голов списков будет хранить указатели на списки ненулевых элементов строк.

Иногда полезны упаковки, не использующие связанных списков. Для них требуется меньшая память, но добавление и удаление ненулевых элементов требует сдвига элементов массива. Ниже описываются четыре такие схемы.

1. Опис розреженої матриці.

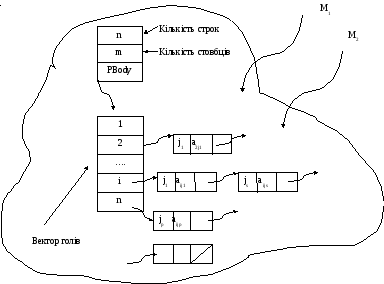
Рис.2 Опис розреженої матриці за упакованою схемою.

Зауваження: Список при описі матриці може бути упорядкованим та не упорядкований. Рекомендують зберігати в упорядкованому списку за номерами стовбців.

2. Опис типу на мові програмування.

type

PNode=^Node;

Node=record

j: word;

el: real;

next:PNode;

end;

Ptrarray=array[1..65520divsizeof(PNode)] of PNode;

Matr=recordо

n,m:word;

Pbody: Ptrarray;

end;

PMatr=^Matr;

Щоб приступити до реалізації, перше, що необхідно зробити- описати функцію абстракції та інваріант представлення.

Функція абстракції є: Типічна прямокутна матриця є:

Інваріант представлення- вимога до правильного представлення

об’єкту.

В нашому випадку

/* функція інваріант представлення є:

<розмір вектору & < в списку для всіх >&<в списку для різних вузлів для всіх > */

Після даного опису можна описувати інтерфейс об’єкту.

б) Использование одномерных массивов (векторов)

Схема I

Каждому ненулевому элементу матрицы соответствует запись, занимающая две ячейки памяти.

< Номер строки, Значение элемента >

Нуль в первой ячейке означает конец данного столбца. Вторая ячейка в этом случае содержит номер следующего столбца. Нули в обеих ячейках указывают на конец массива, хранящего матрицу. Число ячеек, необходимых для хранения матрицы, рассчитывается по формуле

2 (n + τ +1)

Рассмотрим эту схему на примере матрицы

┌ ┐

│ 0 0 a₁₃ 0 0 │

│ a₂₁ 0 0 a₂₄ 0 │

A₅ = │ 0 0 a₃₃ 0 0 │

│ a₄₁ 0 0 0 a₄₅ │

│ 0 a₅₂ 0 0 0 │

└ ┘

Эта матрица для которой τ = 7, n = 5 будет храниться в виде массива

(0, 1; 2, a₂₁; 4, a₄₁; 0, 2; 5, a₅₂; 0, 3; 1, a₁₃; 3, a₃₃; 0, 4; 2, a₂₄; 0, 5; 4, a₄₅; 0, 0)

Всегда номер строки признак начала столбца признак конца

0 1 2 а₂₁ 4 а₄₁ 0 2 5 а₅₂ 0 0 0

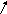
Номер

столбца, представление I-го столбца

где есть

не нулевые элементы

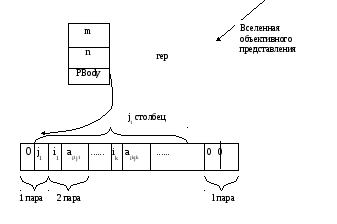
Нумеруем пары для вычисления размера вектора:

ℓ=(n+1+r)-максимальный размер числа пар

r-должно храниться в образе матрицы или вычисляться, но может храниться и в

дискрипторе.

Описываем тип: (В этом случае возникает проблема в том,что j_i-целое, a_ij1-может быть любым,поэтому использование значений этих пар разное при этом используется тип запись с вариантами)

type

Para=record

case K: word of тип i-й пары , она может быть 0 j_i

0: (j:word); i a_iji

else (val: real); (_ _ _ _ _; _ _ _ _ _ );

end;

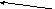
Схема II

Информация о данной матрице хранится в трех массивах: VE – значения ненулевых элементов, RI –индексов строк и CIP – указателей индексов столбцов. Элемент RI(α) содержит индекс строки α-ого элемента VE - VE(α). Если первый ненулевой элемент β-ого столбца данной матрицы размещается в VE(t_β), то t_β хранится в β-ом элементе CIP, т.е. CIP(β) = t_β. Очевидно, VE и RI состоят из τ элементов, а CIP из n элементов. Следовательно эта схема требует общее число в 2τ + n ячеек.

Матрица A₅ будет храниться следующим образом:

VE = (a₂₁, a₄₁, a₅₂, a₁₃, a₃₃, a₂₄, a₄₅)

RI = (2, 4, 5, 1, 3, 2, 4)

CIP = (1, 3, 4, 6, 7)

Вышеизложенной схемой легко пользоваться. Например, a₃₃ может быть найдено следующим образом. Так как CIP(3) = 4, то RI(4) даст индекс строки первого ненулевого элемента третьего столбца. Если a₃₃ ≠ 0, то RI(4) или один из следующих за ним элементов RI предшествующих первому ненулевому элементу четвертого столбца, должен быть равен 3. В нашем случае RI(5) = 3, т.к. VE(5) содержит a₃₃.

Схема III

Каждому ненулевому элементу данной матрицы однозначно ставится в соответствие целое число λ(i, j) вида

λ(i, j) = i + (j – 1)n, a_ij ≠ 0

Хранение ненулевых элементов обеспечивается двумя массивами: VE – значений ненулевых элементов и LD, в каждом из которых содержится τ элементов. В LD(α) находится λ(i, j), соответствующее a_ij из VE(α), где α = 1,2, …, τ.

Матрица A₅ хранится в виде

VE = (a₂₁, a₄₁, a₅₂, a₁₃, a₃₃, a₂₄, a₄₅)

LD = (2, 4, 10, 11, 13, 17, 24)

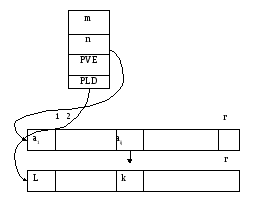
Элементы хранятся по столбцам.

PVE-элементы;

PLD-приведенный индекс элемента в сплошном представлении по столбцам.

Исходная матрица может быть восстановлена по этой схеме хранения следующим образом. В соответствии с данным выше определением для λ(i, j) является очевидным, что j есть наименьшее целое, большее или равное λ(i, j)/n и i = λ(i, j) – (j -1)n.

Например, если λ(i, j) = LD(5) = 13, тогда λ(i, j)/n =13/5 и наименьшее целое число большее или равное λ(i, j)/n будет 3 и i = λ(i, j) – (j -1)n = 13 – 10 = 3.

Схема IV

Если A – симметричная матрица, в которой для всех i ≥ j a_ij = 0, i – j > θ_i, где θ_i намного меньше n и в общем случае может иметь различные значения для каждого i, то такая матрица называется симметричной ленточной матрицей с локально изменяющейся шириной ленты.

В такой матрице можно запоминать только элементы на главной диагонали и ниже. Хранится матрица в виде двух массивов:

VE – значения ненулевых элементов и

PD – положение диагональных элементов в массиве VE.

Для каждой строки в VE хранятся крайний левый ненулевой элемент и все следующие элементы, расположенные справа от него вплоть до диагонального включительно. Поэтому i-ая строка матрицы A требует θ_i + 1 ячеек для хранения и VE будет состоять из n

∑ θ_i + 2n ячеек для хранения матрицы A.

i=1

Например, пусть у нас имеется матрица

┌ ┐

│ a₁₁ 0 0 0 0 │

│ a₂₁ a₂₂ 0 0 0 │

A₅ = │ 0 a₃₂ a₃₃ 0 0 │

│ 0 a₄₂ 0 a₄₄ 0 │

│ 0 a₅₂ a₅₃ 0 a₅₅ │

└ ┘

Тогда ее можно представить в виде

1 2 3 4 5 6 7 8 9 10 11 12

VE = (a₁₁, a₂₁, a₂₂, a₃₂, a₃₃, a₄₂, 0, a₄₄, a₅₂, a₅₃, 0, a₅₅)

PD = (1, 3, 5, 8, 12)

Элемент a_ij исходной матрицы может быть восстановлен следующим образом. Положение a_ij в VE определяется значением PD(i) – (i – j), если только PD(i) – (i – j) > PD(i – 1). Последнее условие означает, что a_ij не будет лежать влево от первого ненулевого элемента i-ой строки, иначе a_ij = 0 и не хранится в VE.

Например, чтобы найти элемент a₅₃ в массиве VE, вычисляем PD(5) – (5 – 3) = 12 – 2 = 10 > 8 = PD(4) и, следовательно, a₅₃ хранится в VE(10).

Главное преимущество этой схемы упаковки состоит в следующем. Если в процессе вычислений, например, при исключениях по методу Гаусса, создаются дополнительные ненулевые элементы только вправо от крайнего левого элемента каждой строки, то они могут запоминаться в VE без перемещений всех следующий за ними элементов.

Диагональная блочная форма (BDF)

Матрица A определенная формулой

┌ ┐

│ A₁₁ A₁₂ … A_1,p-1 A_1,p │

│ 0 A₂₂ … A_2,p-1 A_2,p │

A = │ 0 0 … │

│ … … … │

│ 0 0 … A _p-1,p-1A _p-1,p │

│ A_p1 A_p2 … A _p,p-1 A _p,p │

└ ┘

Имеет форму BDF, если для всех i ≠ j подматрицы A_ij = 0 и все диагональные подматрицы A_ij являются квадратными матрицами.

Треугольная блочная форма (BTF)

Матрица A задана в виде

┌ ┐

│ A₁₁ A₁₂ … A_1,p-1 A_1,p │

│ 0 A₂₂ … A_2,p-1 A_2,p │

A = │ 0 0 … │

│ … … … │

│ 0 0 … A _p-1,p-1A _p-1,p │

│ A_p1 A_p2 … A _p,p-1 A _p,p │

└ ┘

причем подматрицы A_ij = 0 для i ≠ p и подматрицы A_ii, i = 1, 2, …, p являются квадратными матрицами, то говорят, что матрица A имеет треугольную блочную форму BTF.

Треугольная ленточная форма (BNTF)

Говорят, что матрица B имеет треугольную ленточную форму, если существует такое β 0 ≤ β ≤ n, где b_ij = 0 для всех i – j > β, и значение β не может быть уменьшено перестановками строк и столбцов матрицы B.

Пусть первый ненулевой элемент i-ой строки матрицы B находится в q_i-ом столбце. Тогда определяем

β _i = i- q_i, q_i ≤ i

β _i = 0, q_i > i

Очевидно, что если матрица B имеет форму BNTF, то max β _i = β .

Заметим, что треугольная блочная форма (BTF), описанная в предыдущем разделе, является специальным случаем BNTF (β + 1 является в этом случае размером наибольшего диагонального блока матрицы B).

Ленточная форма (BF)

Определение. Матрица A, у которой a_ij = 0 при |i – j| > β, называется ленточной матрицей. Если к тому же a_ij ≠ 0 для всех |i – j| ≤ β, то она называется полной ленточной матрицей. Величина 2β + 1 называется шириной ленты.