MRO / ТМРО_513

Лабораторная работа №3

МАРКОВСКИЕ МОДЕЛИ.

Цель: усвоить основы применения Марковских моделей.

Основные теоретические сведения.

Происходящие явления можно описывать как сигналы. Сигналы могут быть дискретными, как письменная речь, или непрерывными, как фонограмма или кардиограмма. Сигналы с постоянными статистическими свойствами называются стабильными (стационарными), а с меняющимися — нестабильными (нестационарными). Сигнал может быть чистым, а может и искаженным, с помехами или посторонними сигналами.

Для описания сигналов часто нужны математические модели. В модели сигнала на основе его характеристик может быть предусмотрен определенный механизм обработки, который позволяет получить желаемый выход при анализе сигнала. Например, если надо облагородить сигнал, искаженный и зашумлённый при передаче, мы можем смоделировать его и рассмотреть эту модель отвлечённо от искажений и шумов в сигнале. Модели позволяют также генерировать и исследовать сигнал без его источника. В этом случае, имея под рукой хорошую модель, мы можем имитировать сигнал и изучить его по этой имитации.

Модели очень успешно применяются на практике, позволяя создавать эффективные рабочие системы: системы прогноза, распознавания, идентификации.

Марковская цепь задается начальным распределением вероятностей и вероятностями перехода . – это распределение следующего элемента цепи в зависимости от предыдущего; распределение на (t+1)-м шаге равно

В дискретном случае . – это матрица переходов между состояниями . Предполагается рассмотрение только дискретных задач. С помощью марковской модели можно моделировать марковский процесс, при этом подразумевается, что мы можем наблюдать какие-то функции от марковского процесса.

Скрытые марковские модели предполагают, что состояния и связи между ними – неизвестны (скрытые параметры модели). Известно лишь наблюдаемая величина y(t), которая зависит от скрытых переменных x(t), рис. 1. Задача заключается в том, чтобы определить скрытые параметры процесса. Иными словами, по имеющимся данным y(t) необходими понять, каковы наиболее вероятные x(t) и наиболее вероятная модель этого марковского процесса.

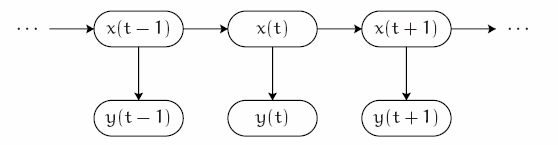
Рис. 1-Дискретный марковский процесс

Главное свойство скрытой марковской модели первого порядка – это то, что текущее состояние зависит только от предыдущего. Формально это значит, что вероятность x(t) при условии всех остальных установленных значений равна вероятности x(t) при условии только предыдущего значения:

Кроме того, вероятности не зависят от времени t. Эти вероятности составляют матрицу перехода .

Для вероятностей перехода ад выполняются следующие естественные свойства:

-

- (если мы начнём в состоянии і, то куда-нибудь мы точно попадём).

Постановка задачи

Прямая задача заключается в определении того, с какой вероятностью вьпадет та или иная последовательность событий Q=q_i1, q_i2, …q_ik. Если Q - это последовательность состояний марковской цепи, то отыскание её вероятности не составляет никакого труда:

p(Q|модель) = p(q_i1)p(q_i2| q_i1)p(q_ik|q_ik-1)

Но реальные задачи гораздо сложнее. Сложность в том, что никто нам не скажет, что модель должна быть именно такой. Мы обычно наблюдаем не ×(t), т.е. реальные состояния модели, а у(t), т.е. некоторую функцию от них (данные).

Давайте рассмотрим пример. Предположим, что кто-то бросает монетку и сообщает нам результаты - последовательность орлов и решек. Но при этом подбрасыва е монетки происходит где-то там, в другой комнате, поэтому мы только знаем, что есть определённая последовательность битов. Если он бросает одну монетку, то модель будет выглядеть следующим образом (см. рис. 2а) Будет два состояния: 0 (выпал орёл) и 1 (выпала решка). С вероятностью 1 -р выпадает орёл, с вероятностью р - решка. Это одна модель.

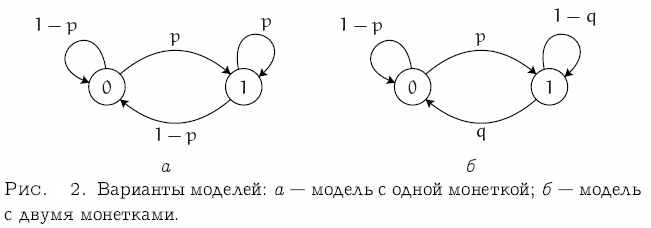
Рис. 2 Варианты моделей: а – модель с одной монеткой; б – модель с двумя монетками.

Но мы же можем подумать, что у него две монетки! Он кидает монетку. Когда у него выпадает решка, он переходит на другую монетку. Когда у него выпадает орёл на другой монетке, он возвращается к подбрасыванию первой монетки. В данном случае уже две вероятности: р и q. Модель уже совершенно другая (см. рис. 2б). В ней по-прежнему два состояния, но параметров больше. А если три монетки? Наша задача в том числе и в том, чтобы понять, какая и3 этих моделей лучше соответствует известным данным.

Проблемы решения СММ

Рассматриваются три основные задачи, которые необходимо решить для использования модели в реальных задачах:

Первая: найти вероятность последовательности наблюдений в данной модели.

Вторая: найти «оптимальную» последовательность состояний при условии данной модели и данной последовательности наблюдений.

Третья: найти наиболее правдоподобную модель (параметры модели).

Проблема 1 является обычной задачей оценивания. Известны модели и последовательность наблюдений. требуется вычислить вероятность того, что наблюдения порождены заданной моделью. Можно также рассматривать эту проблему как задачу выяснения. насколько хорошо некоторая модель подходит к имеющейся последовательности наблюдений. Последняя точка зрения часто оказывается полезна. Например. в случае существования сразу нескольких возможных моделей, решение проблемы І позволяет выбрать именно ту, которая наилучшим образом соответствует имеющимся наблюдениям.

Проблема 2 связана с тем. каким образом можно «открыть» скрытую часть модели. т. е. найти «правильную» последовательность состояний. Очевидно, что при заданной последовательности наблюдений и известной модели нельзя найти абсолютно точную последовательность состояний, соответствующих наблюдениям, за исключением того вырожденного случая, когда имеющаяся последовательность наблюдений порождена именно этой моделью. Поэтому на практике определение последовательности состояний обычно делается с использованием некоторого критерия оптимальности. К сожалению, как мы увидим ниже. существует сразу несколько приемлемых критериев оптимальности, поэтому выбор того или иного из них в значительной мере зависит от целей дальнейшего использования полученной последовательности состояний. Типичной целью может, например, быть изучение структуры модели, поиск оптимальной последовательности состояний для распознавания слитной речи и т. п.

Проблема 3 представляет собой задачу. в которой мы пытаемся оптимизировать значения параметров, для того чтобы модель наилучшим образом соответствовала имеющимся наблюдениям. Последовательность наблюдений. используемая для подстройки параметров, называется обучающей последовательностью, поскольку она используется для «обучения» СММ. Проблема обучения очень важна для большинства приложений, так как именно во время обучения происходит, в соответствии с выбранным критерием оптимальности, подстройка значений параметров модели по данным наблюдении, в результате чего создается модель, наилучшим образом соответствующая реальному явлению.

Обозначим полный набор параметров Θ={π,A,φ}. Тогда основные задачи, возникающие в СММ, можно сформулировать следующим образом:

Обучение с учителем. Известна некоторая последовательность Х, для которой заданы Т. Задача состоит в оценке по обучающей выборке набора параметров Θ.

Сегментация. Известна некоторая последовательность Х и набор параметров Θ. Задача состоит в получении наиболее правдоподобной последовательности состояний Т как arg max_T p(T|X,Θ) (алгоритм Витерби).

Обучение без учителя. Известна некоторая последовательность Х и число состояний К. Задача состоит в оценке параметров Θ (ЕМ-алгоритм). Нахождение маргинального распределения p(t_n|X,Θ) компоненты t_n по заданным Х и Θ.

Прогнозирование. Известна некоторая последовательность Х. Задача состоит в оценке наблюдаемого вектора в следующий момент времени N + 1 - р(х_N+1|Х)

Задание.

Реализовать применить Марковской модели для любой задачи распознавания.