
- •Векторна алгебра
- •Системи лінійних алгебраїчних рівнянь. Метод послідовного виключення невідомих (метод Гаусса).
- •Поняття вектора, лінійні операції над векторами.
- •Поняття лінійно залежних і лінійно незалежних систем векторів.
- •Геометрична інтерпретація поняття лінійної залежності.
- •Поняття базису простору і площини
- •Афінна система координат.
- •Додатковий матеріал з векторної алгебри
- •Поняття лінійного простору.
- •Найпростіші властивості векторного простору.
- •Теорія визначників n-го порядку.
- •Перестановки з n символів.
- •Підстановки n-го степеня.
- •Поняття і властивості визначника n-го порядку
- •Мінори і алгебраїчні доповнення визначника
- •Лема до теореми Лапласа. Теорема Лапласа.
- •Застосування теорії визначників до лінійних систем алгебраїчних рівнянь. Теорема Крамера та лема до неї
- •Векторний простір
- •Подальше вивчення векторного простору.
- •Поняття рангу системи векторів.
- •Поняття рангу матриці. Теорема про ранг матриці.
- •Загальна теорія лінійно-алгебраїчних рівнянь
- •Критерій сумісності лінійних алгебраїчних рівнянь
- •Критерій визначеності і невизначеності системи
- •Однорідна система рівнянь. Фундаментальна система розв'язків однорідної системи рівнянь.
- •Зв’язок між розв’язком неоднорідної і відповідної однорідної системи рівнянь.
- •Алгебра матриць
- •Множиння матриць.
- •Матриці обернені до даних. Умови їх існування.
- •Операції додавання і множення на число.
- •Скалярні матриці.
- •Операції над прямокутними матрицями.
- •Псевдообернені матриці.
- •Комплесні числа.
- •Побудова множини комплексних чисел.
- •Полярна система координат.
- •Тригонометрична форма комплексного числа. Операції множення та ділення в тригонометричній формі.
- •Операції піднесення до степеня
- •Операція здобуття кореняn-ого степеня з комплексного числа
- •Кореніn-ого степеня з одниці
- •Комплексно-спряжені числа
- •Нерівність трикутника
- •Література
Підстановки n-го степеня.
Означення. Підстановкою
![]() -го
степеня називається бієктивне відображення
-го
степеня називається бієктивне відображення
![]() -елементної
множини у себе.
-елементної
множини у себе.
Будемо
записувати підстановку у два рядки: у
першому будуть вихідні ![]() елементів, а у другому – їх образи.
елементів, а у другому – їх образи.
Наприклад:
![]()
Поставимо 2 питання:
Скільки форм запису однієї ї тієї підстановки.
Скільки різних підстановок n-го степеня можна скласти.
На
обидва питання відповідь:![]()
Розглянемо перше питання. Різні форми запису можна отримати за рахунок різного розташування стовпчиків перестановок. З теорії перестановок відомо, що їх буде n!.
Розглянемо друге питання. Зафіксуємо елементи у першому рядку. Очевидно, що підстановки будуть різними, якщо відрізняються відповідно образи у другому рядку. Отже кількість підстановок дорівнюватиме кількості перестановок елементів другого рядка, а їх, як відомо, n!.
Означення. Підстановка називається парною, якщо парності верхньої і нижньої перестановок однакові, тобто обидві перестановки або парні або непарні.
Означення. Підстановка називається парною, якщо загальна кількість інверсій верхньої і нижньої перестановок є парним числом, в супротивному разі перестановка непарна.
Теорема. Приn≥2
кількість парних підстановок дорівнює
кількості непарних підстановок, тобто
дорівнює![]() .
.
Запишемо всі підстановки увигляді:

Твердження
теореми випливає з відповідної теореми
для перестановок. Дійсно, тоді
парність підстановки визначається лише
парністю нижньої перестановки, а парних
нижніх існує ![]() .
.
Зауваження. Для самостійного доведення залишається факт, що означення парності підстановки не залежить від форми запису цієї підстановки.
Поняття і властивості визначника n-го порядку
На практичних заняттях було введено поняття визначника другого і третього порядків. Це були числа, отримані за певними законами з таких таблиць- матриць другого і третього порядків відповідно:
![]()
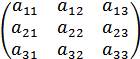
Визначник
другого порядка – це число, що позначається
![]() і яке дорівнює
алгебраїчній
сумі
і яке дорівнює
алгебраїчній
сумі ![]() ,
аналогічно визначник третього порядку:
,
аналогічно визначник третього порядку:
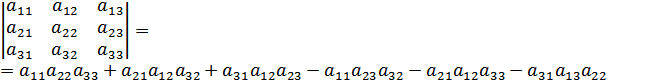
Ми
хочемо узагальнити це поняття, тобто
отримати визначник ![]() -го
порядку таким чином, що з нього при
-го
порядку таким чином, що з нього при ![]() та
та ![]() отримати попереднє.
отримати попереднє.
Аналіз обчислення визначників другого і третього порядків приводить до доцільності такого означення:
Означення. Визначником
![]() -го
порядку, що відповідає матриці:
-го
порядку, що відповідає матриці:
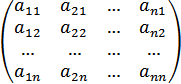
називається
алгебраїчна сума ![]() доданків, кожний з яких є добутком
доданків, кожний з яких є добутком ![]() елементів, взятих по одному з кожного
рядка і кожного стовпця матриці, причому
зі знаком "+", якщо підстановка
складена з перших і других індексів,
парна і зі знаком "–", якщо вона
непарна.
елементів, взятих по одному з кожного
рядка і кожного стовпця матриці, причому
зі знаком "+", якщо підстановка
складена з перших і других індексів,
парна і зі знаком "–", якщо вона
непарна.
Отже
визначник ![]() -го
порядку складається з
-го
порядку складається з![]() доданків вигляду
доданків вигляду![]() ,
де
,
де![]() –кількість інверсій у перестановці
α1,α2,…,αn.
–кількість інверсій у перестановці
α1,α2,…,αn.
Для визначника вводять позначення:

Властивість 1. Визначник не зміниться, якщо його рядки зробити відповідними стовпцями.
Розглянемо визначник d.
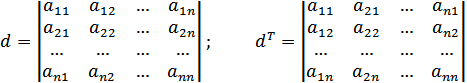
Стверджується, що ![]()
Розглянемо загальний член
визначника d:
(1)
![]() – загальний член
d.
α1,α2,…,αn
- перестановка з 1,2,…,n
Запишемо член
(1) в позначках ij.
– загальний член
d.
α1,α2,…,αn
- перестановка з 1,2,…,n
Запишемо член
(1) в позначках ij.
![]()
![]() (1)
Таким
чином (1) є членом і визначника d1.
З′ясуємо, з яким знаком (1) входить до
визначника d1.
Знак члена (1) в d визначається парністю
підстановки
(1)
Таким
чином (1) є членом і визначника d1.
З′ясуємо, з яким знаком (1) входить до
визначника d1.
Знак члена (1) в d визначається парністю
підстановки
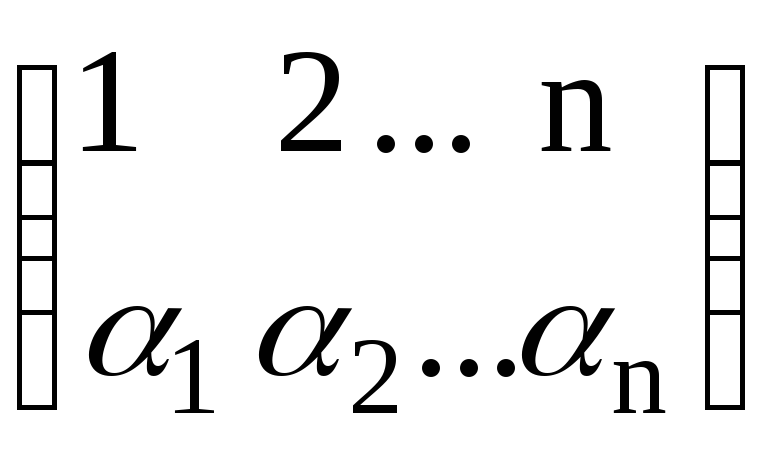 Знак
(1) в d1
визначається парністю підстановки
Знак
(1) в d1
визначається парністю підстановки
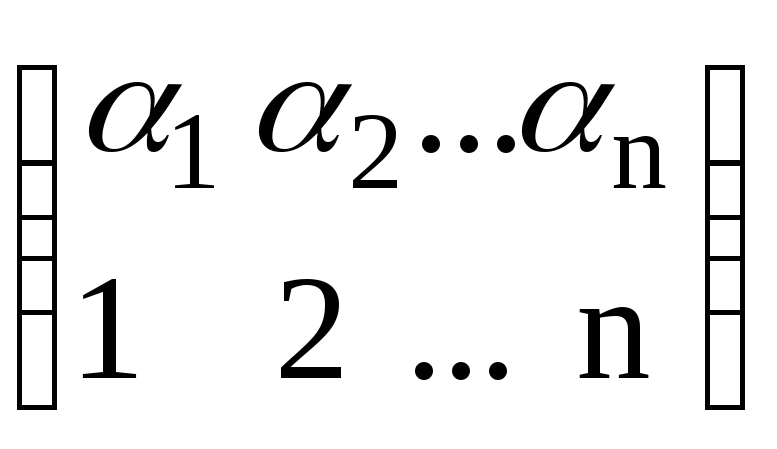 Ці
підстановки, взагалі кажучи, різні, але
парності в них однакові, тому що загальна
кількість інверсій верхньої і нижньої
перестановок однакова, тому і знаки
члена (1) в d і d1
однакові.
Ці
підстановки, взагалі кажучи, різні, але
парності в них однакові, тому що загальна
кількість інверсій верхньої і нижньої
перестановок однакова, тому і знаки
члена (1) в d і d1
однакові.
Це перетворення, при якому всі рядки стають відповідними стовбцями, називається транспонуванням.
Властивість 2. Якщо в визначнику поміняти місцями будь які 2 рядки, то знак визначника зміниться на протилежний.
Доведення за схемою властивості 1.
Насправді, нехай у визначнику![]() міняються місцями i-ий
та j-ий
рядки,
міняються місцями i-ий
та j-ий
рядки,
![]() ,
а всі інші рядки залишаються на місці.
Ми отримаємо визначник
,
а всі інші рядки залишаються на місці.
Ми отримаємо визначник![]() :
:
 .
.
Якщо
![]() (1)
є членом визначника
(1)
є членом визначника![]() ,
то всі його елементи і у
визначнику
,
то всі його елементи і у
визначнику
![]() залишаються, очевидно, в різних рядках
і різних стовпцях. Таким чином, визначникиdтаd1складаються з одних і тих же
членів.
залишаються, очевидно, в різних рядках
і різних стовпцях. Таким чином, визначникиdтаd1складаються з одних і тих же
членів.
Члену (1) у визначнику![]() відповідає
підстановка
відповідає
підстановка (2),
(2),
а
у визначнику
![]() -
підстановка
-
підстановка (3).
(3).
Підстановку (2) можна одержати з підстановки (1) однією транспозицією в верхньому рядку, тобто вона має протилежну парність. Звідси випливає, що всі члени визначника d входять до визначника d1 і відрізняються лише знаком.
Властивість 3. Якщо в визначнику є нульовий рядок, то визначник дорівнює 0.
Нехай усі елементи і-го рядка визначника є нулями
За означенням визначник n-го порядку це алгебраїчна сума n доданків, кожний з яких є добутком n елементів, узятих по одному з кожного рядка й кожного стовпця матриці і т.д. Отже, у кожний член визначника повинен увійти множником один елемент з і-ого рядка, тому в нашому випадку всі члени визначника дорівнюють нулю. Що й треба було довести.
Властивість 4. Якщо в визначнику є 2 рівних рядка, то визначник дорівнює 0.
Доведення. Нехай у визначнику d рівні між собою і-рядок і j=рядок
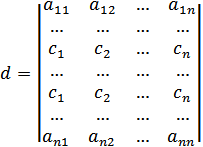
Нехай d=k
d1–визначник d, в якому поміняли і з j рядок.
Тоді за властивістю 2:
d1=-k
Але насправді нічого не змінилось, оскільки, i та j рядки рівні
d1=d=k ⟹ -k=k
Звідси, 2k=0, k=0.
Властивість 5. Якщо всі елементи деякого рядка помножити на числоr, то визначник зміниться вrразів.
Доведення за схемою властивості 1.
Цю ж властивість можна сформулювати у вигляді: якщо рядок визначника містить постійний множник, то його можна винести за знак визначника.
Розглянемо визначник d:
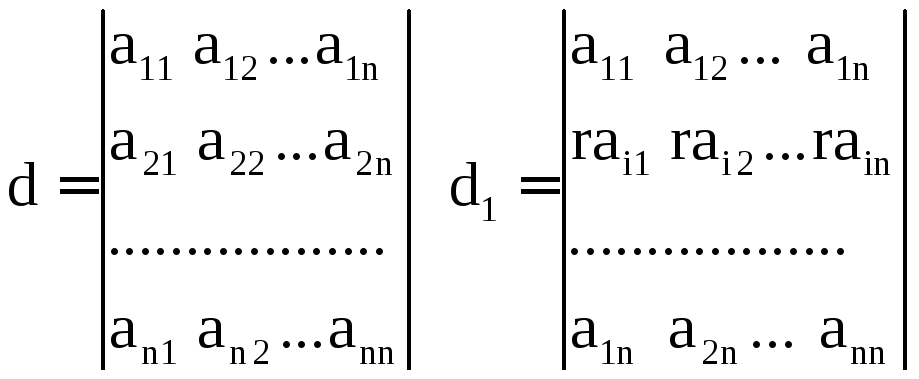
![]()
Нехай на r помножені всі елементи і-ого рядка. Кожний член визначника містить рівно один елемент із і-ого рядка, тому всілякий член отримує множник r, тобто сам визначник множиться на r.
Властивість 6. Якщо у визначнику є два пропорційні рядки, то визначник = 0.
Доведення проводиться з використанням властивості 5 і властивості 4.
Насправді, нехай елементи
j-ого рядка
визначника відмінюються від відповідних
елементів і-ого рядка
![]() одним і тим самим множникомr.
одним і тим самим множникомr.
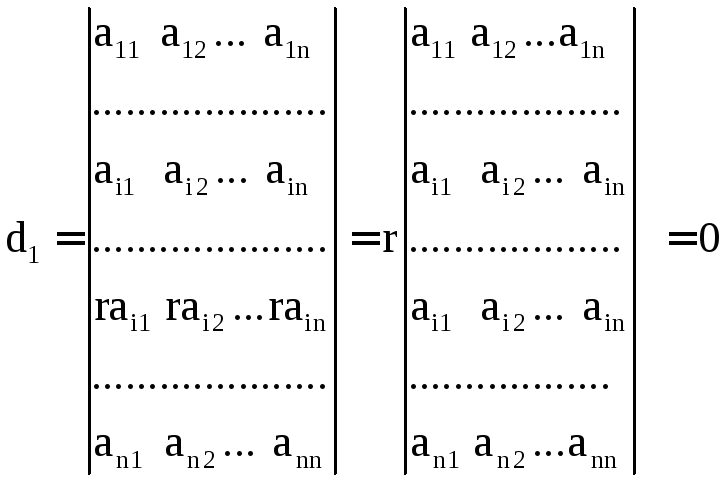
Виносячи спільний множник r із j-ого рядка за знак визначника, ми отримуємо визначник з двома однаковими рядками, який дорівнює нулю за властивістю 4.
Властивість 4 (а також
властивість 3 при
![]() )
є, очевидно, окремим випадком властивості
6 (приr= 1 і
r= 0).
)
є, очевидно, окремим випадком властивості
6 (приr= 1 і
r= 0).
Властивість 7. Якщо кожний елемент і-рядка визначників є сумою 2-ох доданків, то такий визначник можна подати як суму двох визначників, у яких всі рядки, за винятком і-ого такі ж, як у початковому. і-й рядок першого визначника складається з перших доданків, і-ий рядок другого визначника складається з других доданків.
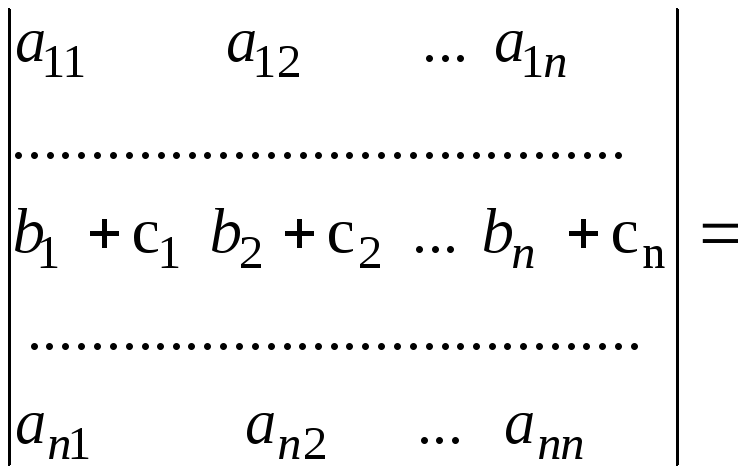
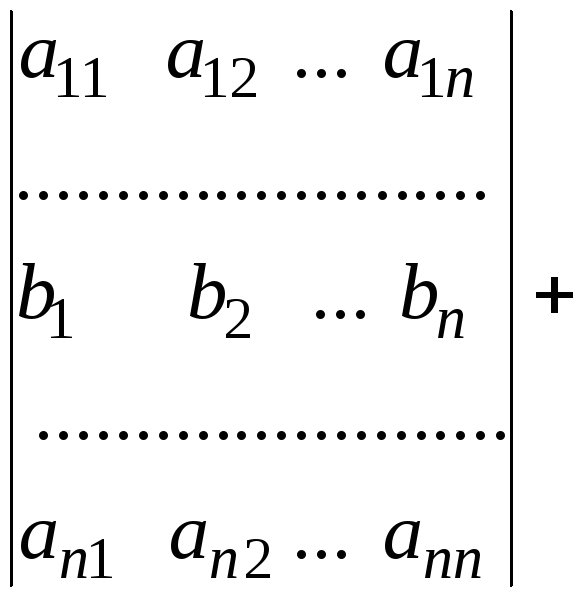
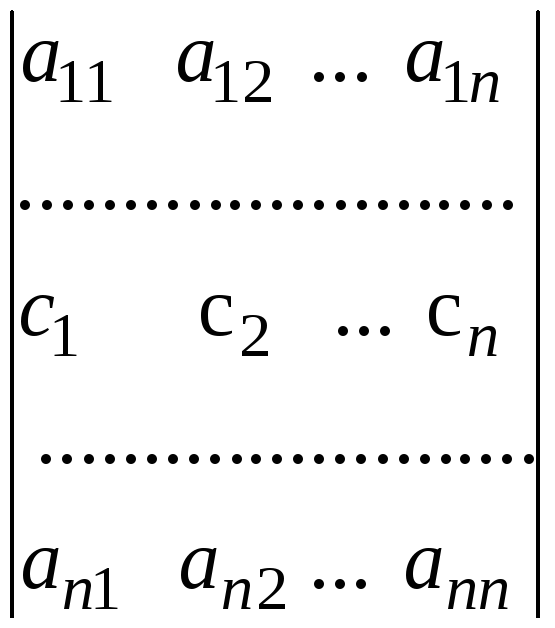
Доведення за схемою доведення властивості 1.
Дійсно, всілякий член заданого визначника можна подати у вигляді:
![]()
Збираючи
разом перші доданки цих сум (з тими ж
знаками, які мали відповідні члени в
заданому визначнику) ми отримаємо,
очевидно, визначник n-го
порядку, що відмінюється від заданого
визначника лише тим, що в і-ому рядку
замість елементів
![]() стоять елементи
стоять елементи![]() .
Відповідно другі доданки складають
визначник, в і-ому рядку якого стоять
елементи
.
Відповідно другі доданки складають
визначник, в і-ому рядку якого стоять
елементи![]() .
.
Властивість 8. Якщо до і-ого рядка визначника додатиj-ий рядок, в подумках помножений на деяке число, то визначник не зміниться.
Доведення.Нехай до і-го рядка визначника d додається
j-ий рядок, помножений на k, тобто в новому
визначнику всілякий елемент і-го рядка
має вигляд![]() .
Тоді на підставі властивості 7 цей
визначник дорівнює сумі двох визначників,
з яких перший є d, а другий містить
пропорційні рядки і тому дорівнює 0.
.
Тоді на підставі властивості 7 цей
визначник дорівнює сумі двох визначників,
з яких перший є d, а другий містить
пропорційні рядки і тому дорівнює 0.
Властивість 9. Якщо в визначнику присутній рядок, що є лінійною комбінацією інших рядків, то визначник дорівнює 0.
Доведення.
Нехай, наприклад, і-ий рядок буде лінійною комбінацією s інших рядків
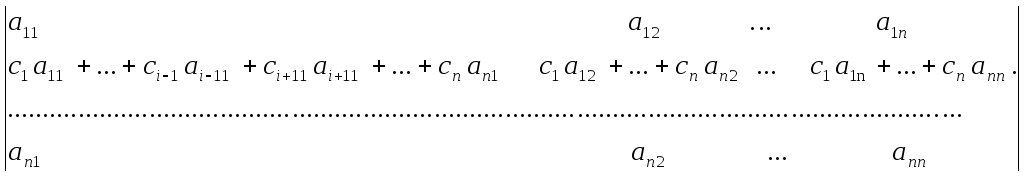
Застосовуючи властивість 7, ми подамо наш визначник у вигляді суми визначників, у кожному з яких і-ий рядок буде пропорційним до одного з інших рядків.
За властивістю 6 усі ці визначники дорівнюють нулю, дорівнює нулю, отже і заданий визначник теж.
Ця властивість є узагальненням властивості 6, причому вона дає найзагальніший випадок рівності визначника нулю.
Зауваження. Завдяки властивості 1 все, що було формульовано для рядків є правильним і для стовпців, тому властивість 1 називається властивістю рівноправності рядків і стовпців.
