4. Зв’язок між розв’язком неоднорідної і відповідної однорідної системи рівнянь.

Нехай задано неоднорідну систему

,(1)

Означення.Відповідною однорідною системою називається система

, (2)

з тими ж самими коефіцієнтами .

Звя’язок між розв’язками системи (1) та (2) описується наступними теоремами.

Теорема 1.Сума розв’язків неоднорідної і відповідної однорідної системи лінійних алгебраїчних рівнянь є розв’язком неоднорідної системи .

Теорема 2. Різниця двох розв’язків неоднорідної системи є розв’язком відповідної однорідної системи.

Доведення теореми 1.Нехай () – розв’язок системи (1), () – розв’язок системи (2). Треба довести , що- розв’язок системи (1) .

За означенням розв’язку маємо систему правильних числових рівностей

, () (3)

, () (4)

Підставимо в ліву частину системи (1) замість .

()

Перша властивість доведена.

Доведення теореми 2.Нехай () , () – розв’язки системи (1). Розглянемо упорядкований набір. Ми повинні довести, що це розв’язок системи (2) .

За означенням розв’язку маємо системи правильних числових рівностей:

, (), (3)

, (). (3’)

Підставимо в ліву частину рівнянь системи (2) замість числавідповідно і обчислимо її.

.

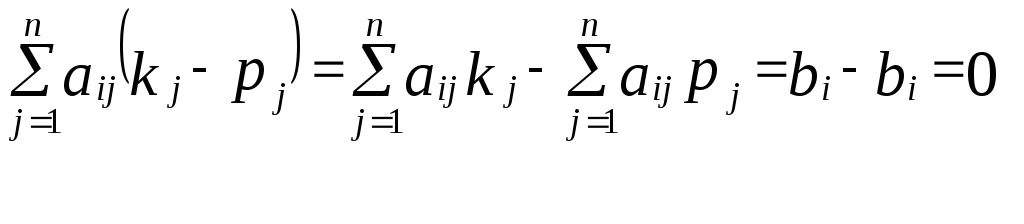Таким чином , одержуємо правильних числових рівностей.

Твердження. З цих двох теорем випливає такий алгоритм розв’язування неоднорідної системи рівнянь : множину всіх розв’язків можна одержати додавання до кожного розв’язку множини розв’язків однорідної системи одного розв’язку (окремого) неоднорідної системи.

Доведенння твердження.

Нехай Н=– множина розв’язків системи (1),

– множина розв’язків системи (2).

Нехай - окремий розв’язок системи (1).

Розглянемо суму з будь-яким розв’язком однорідної системи.

+=** є Н - розв’язок системи (1) .

Виникає питання, може система (1) має інші розв’язки, що отримуються за іншим алгоритмом ? Доведемо, що цього не може бути.

2) Нехай є Н. Доведемо, щоможна одержати додаванням доякогось розв’язку з множиниQ . Розглянемо різницю (-). Тоді за теоремою 2 , це розв’язок системи (2), тобто (-) =* єQ. Отже.

5. Алгебра матриць

Розглянемо спочатку квадратні матриці одного і того ж n- го порядку. Для матриць введено три операції :

1. множиння матриць;

2. додавання матриць;

3. множиння матриці на число.

1. Множиння матриць.

Означення. Добутком матриць А і В називається матриця С того ж самого порядку, що матриці А та В, елементи якої утворюються за таким законом:

елемент розташованний в і-тому рядку та к-му стовпцю матриці С дорівнює сумі добутків елементів і-того рядка матриці А на відповідні елементти к-того стовпця матриці В.

А=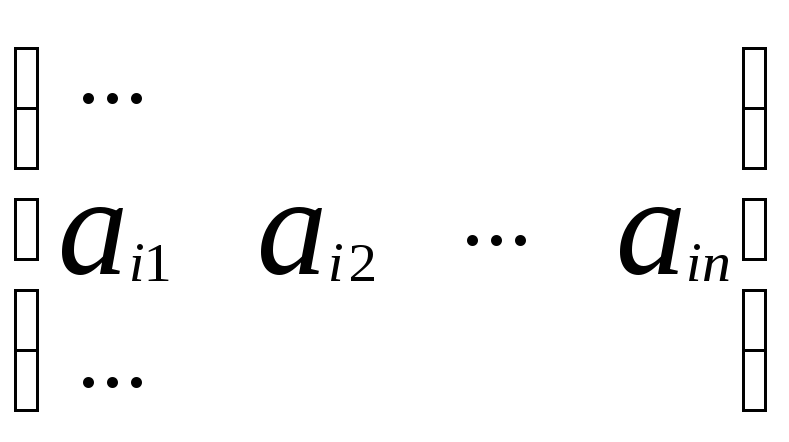, В=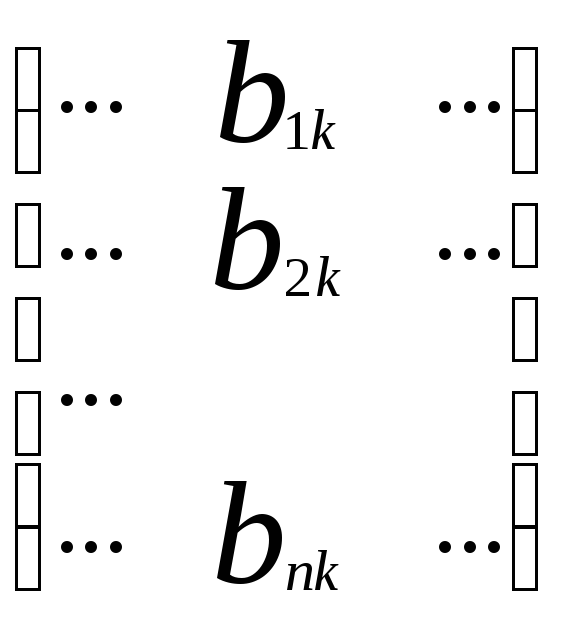

.

Закони множення.

1. Множення матриць, взагалі кажучі, не комутативне. Для того, щоб в цьому переконатись,досить знайти дві матриці А і В, для яких АВ  ВА .

А=, В=.

АВ = =,

ВА = =.

З наведеного прикладу бачимо, що АВ  ВА . При цьому ми виходили з такого означення рівних матриць.

Означення. Матриці А і В називаються рівними, якщо на одних і тих самих місцях знаходяться рівні елементи.

Теорема . Множення матриць підпорядковується асоціативному закону.

Тобто ми повинні довести, що для будь-яких матриць А, В і С має місце рівність

( А  В )  С = А  ( В  С ) .

Нехай

А=() , В=() . А В = D= ()

( А  В )  С = C D=F(), ( В  С ) = Р ()

А  (В  С ) = А Р = Т () .

В цих позначеннях треба довести, що F= Т , тобто (= 1,2,…,)

Обчислимо

, (1)

, (2)

Підставимо (2) в (1) , отримаємо

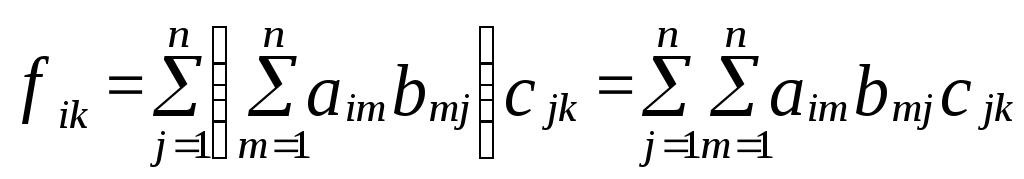(3)

Преходимо до обчислення .

(4)

(5)

Підставимо (5) в (4), отримаємо

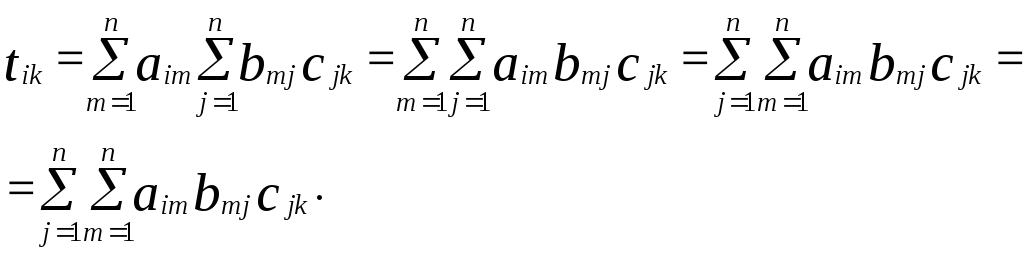(6)

Порівнюючи (3) і (6), приходимо до висавку, що , що й треба було довести .

Хоча множення матриць, взагалі кажучі, некомутативне, існує матриця, яка комутує з будь-якою матрицею А, і більш того, в добутку з даною матрицею не змінює цю матрицю А. Це так звана одинична матриця :

Е = .

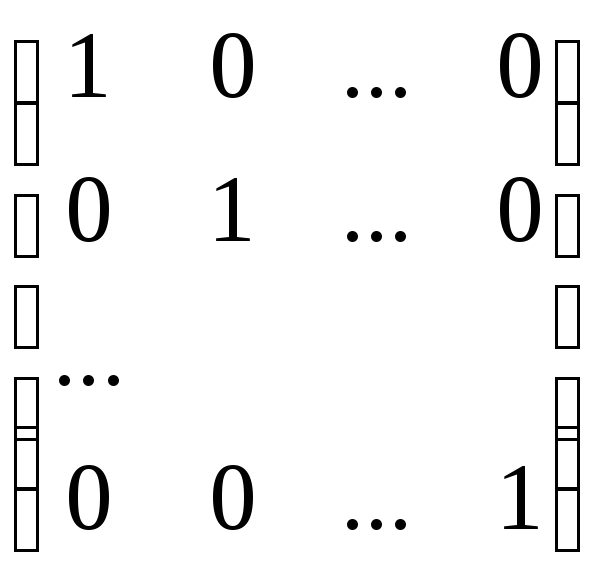Ця матриця має такі властивості :

1) А  Е = А ,  А

2) Е  А = А ,  А ,

а звідси випливає, що А  Е = Е  А .

Доведемо другу властивість.

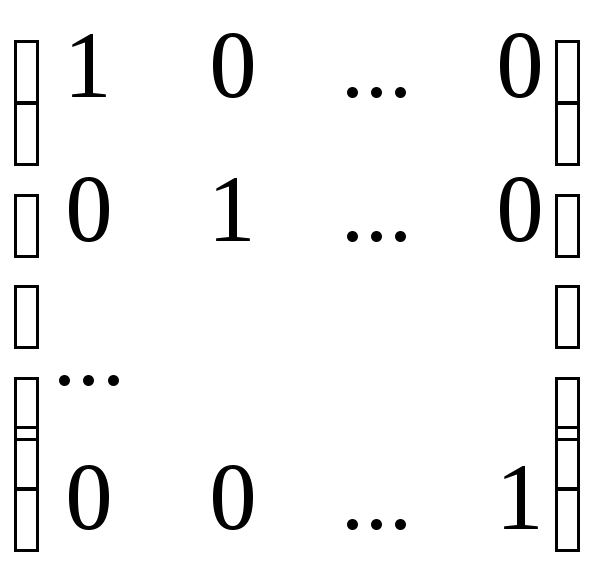
Е  А = =

= = А .

Так само доводиться перша властивість, тобто безпосереднім множенням.

Теорема. .

Доведеня. Нехай задано матриці А і В , а С – добуток цих матриць. Треба довести, що

detC=detAdetB.

Для доведення побудуємо визначник dпорядку 2n:

d= .

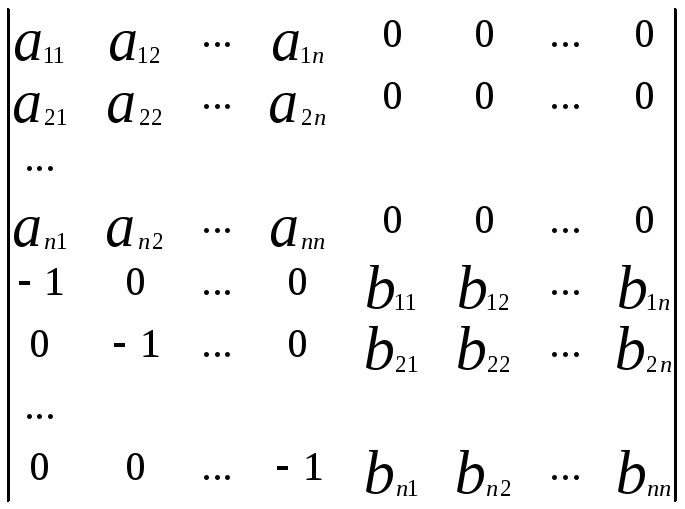Застосуємо до перших n рядків цього визначника теорему Лапласа

d = det A det B (_{, тобто}

d=detAdetB(1)

Перетворимо визначник dза допомогою восьмої властивості визначників. До (n+1) стовпчика додамо перший стовпець помножений на , другий – на , n-ий – на.

Аналогічно зробимо з (n+2)-им стовпцем, (2n)-им стовпцем. В правому нижньому куті отримаємо нульовий блок порядку n. А правий верхній кут, тоді перетворюється в елементи матриці С.

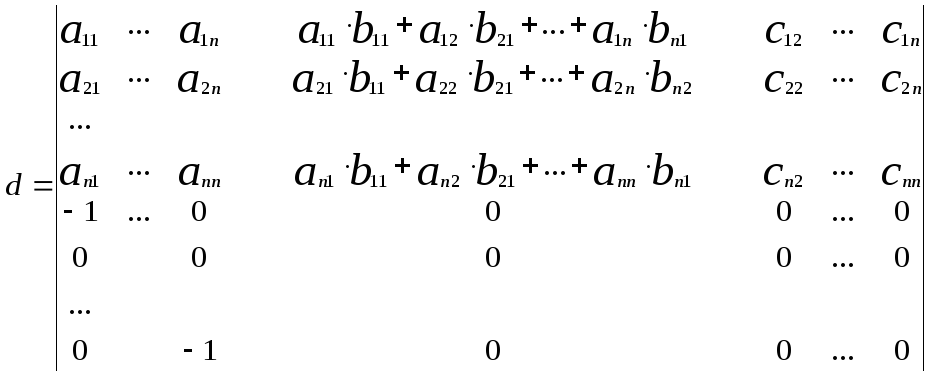
Застосуємо до цього визначника теорему Лапласа .

d=detC .

Користуючись формулою суми 2n членів арифметичної прогресії, маємо

d = det C , det C = det A det B .

Вправа. Довести самостійно єдиність одиничної матриці (скористатись методикою доведення єдиності нульового вектора будь-якого лінійного простору).